山東省諸城市桃林鎮(zhèn)中考數(shù)學(xué) 第13章 統(tǒng)計初步復(fù)習(xí)題（無答案）

《山東省諸城市桃林鎮(zhèn)中考數(shù)學(xué) 第13章 統(tǒng)計初步復(fù)習(xí)題（無答案）》由會員分享，可在線閱讀，更多相關(guān)《山東省諸城市桃林鎮(zhèn)中考數(shù)學(xué) 第13章 統(tǒng)計初步復(fù)習(xí)題（無答案）（6頁珍藏版）》請在裝配圖網(wǎng)上搜索。

1、 第13章 統(tǒng)計初步 ★13．1 有15個正整數(shù)，去掉最大的數(shù)后，平均數(shù)約等于2.5；去掉最小的數(shù)后，平均數(shù)約等于2.8．求最大數(shù)與最小數(shù)之差． ★★13．2 小華計算7個正整數(shù)的平均數(shù)（得數(shù)保留兩位小數(shù)）時，將得數(shù)最后一位算錯了．他的錯誤答案是21.83，則正確答案應(yīng)是多少？ ★13．3 某養(yǎng)魚戶在池塘養(yǎng)魚已三年，頭一年放養(yǎng)鰱魚苗20000尾，其成活率約為70%，在秋季捕撈時，隨意撈出10尾魚，稱得每尾的質(zhì)量如下（單位：kg)： 0.80， 0.9， 1.2， 1.3， 0.8， 0.9，1.1，1.0， 1.2， 0.8． （1）根據(jù)樣本平均數(shù)估計這池魚的總質(zhì)量是多

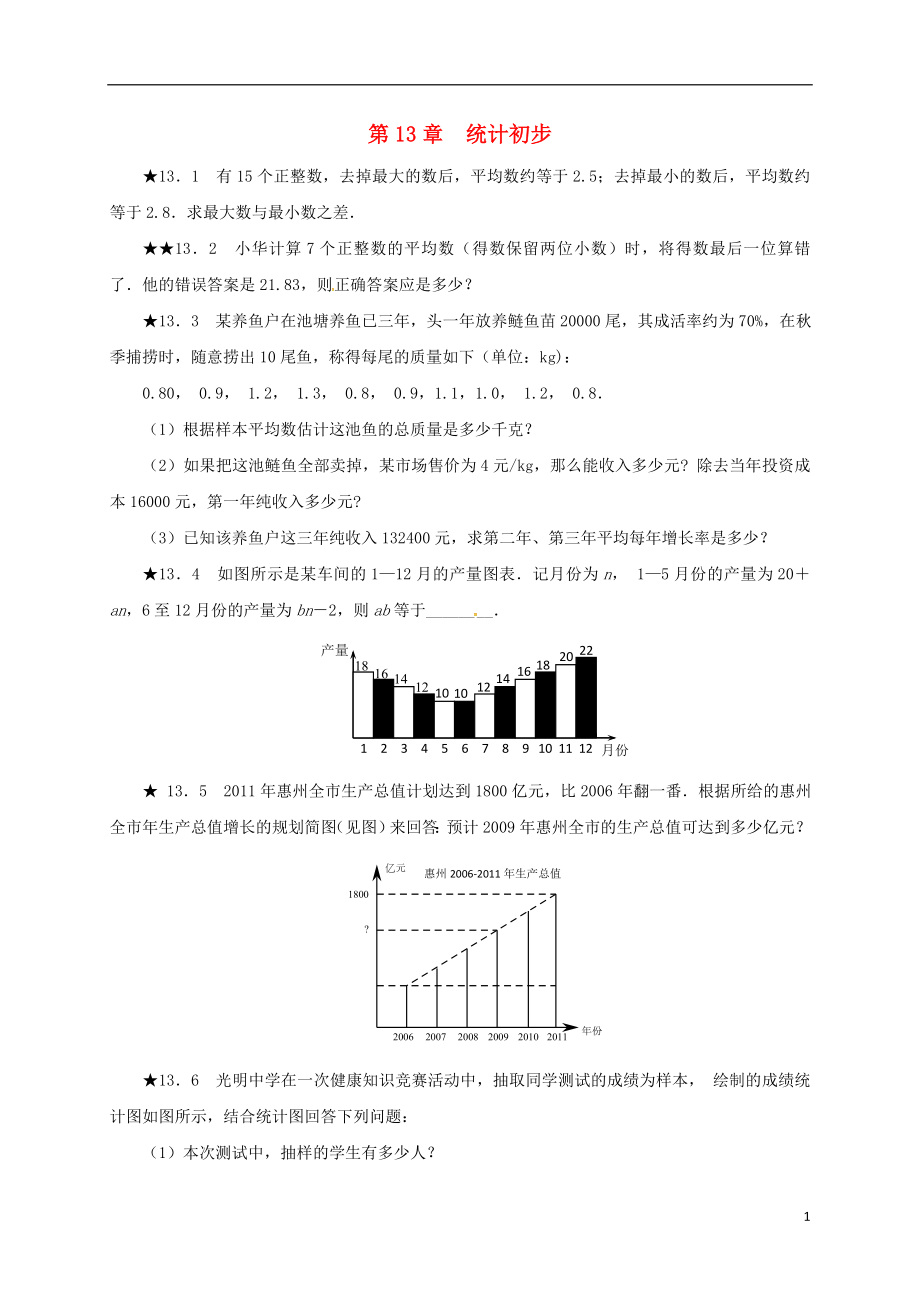
2、少千克？ （2）如果把這池鰱魚全部賣掉，某市場售價為4元/kg，那么能收入多少元? 除去當(dāng)年投資成本16000元，第一年純收入多少元? （3）已知該養(yǎng)魚戶這三年純收入132400元，求第二年、第三年平均每年增長率是多少？ ★13．4 如圖所示是某車間的1—12月的產(chǎn)量圖表．記月份為n， 1—5月份的產(chǎn)量為20＋an，6至12月份的產(chǎn)量為bn－2，則ab等于________． 月份 產(chǎn)量 1 2 3 4 5 6 7 8 9 10 11 12 10 12 14 16 18 20 22 18 16 14 12 10 ★ 13．5 2

3、011年惠州全市生產(chǎn)總值計劃達(dá)到1800億元，比2006年翻一番．根據(jù)所給的惠州全市年生產(chǎn)總值增長的規(guī)劃簡圖（見圖）來回答：預(yù)計2009年惠州全市的生產(chǎn)總值可達(dá)到多少億元？ 惠州2006-2011年生產(chǎn)總值 ★13．6 光明中學(xué)在一次健康知識競賽活動中，抽取同學(xué)測試的成績?yōu)闃颖荆?繪制的成績統(tǒng)計圖如圖所示，結(jié)合統(tǒng)計圖回答下列問題： （1）本次測試中，抽樣的學(xué)生有多少人？ （2）分?jǐn)?shù)在90.5~100.5分這一組的頻率是多少? （3）這次測試成績的眾數(shù)在哪個小組內(nèi)？ （4）若這次測試成績80分以上（含80分）為優(yōu)秀，則優(yōu)秀率不低于多少？ 0 分?jǐn)?shù)/分 人數(shù)/人 60.5

4、 70.5 80.5 90.5 100.5 2 3 4 41 ★13．7 在學(xué)校開展的美術(shù)比賽活動中，某班進(jìn)行作品評比，作品上交時間為5月1一30日，評委會把同學(xué)們上交作品的件數(shù)按5天一組分組統(tǒng)計，繪制了頻率分布直方圖，如圖所示．已知從左至右各長方形的高的比為2:3:4:6:4:1，第三組的頻數(shù)為12，請回答下列問題： （1）本次活動共有多少件作品參加評比？ （2）哪組上交的作品數(shù)量最多？有多少件？ （3）經(jīng)過評比，第四組和第六組分別有10件、2件作品獲獎，問：這兩組中哪組獲獎率較高？ 0 日期/日 1 6 11 16

5、 21 26 31 ★13．8 某個體戶以每件80元的價格進(jìn)了一種服裝100件，在銷售過程中發(fā)現(xiàn)每天銷售的件數(shù)與銷售價相關(guān)，每天以不同銷售價（同一天售價相同）銷售情況如下表所示： 0 售價/元 售價/件 120 115 110 105 100 12 16 20 24 28 每天的支出情況如下表： 支出項(xiàng)目 房租 稅收 員工工資 其它 支出金額/元 100 60 90 30 根據(jù)圖表提供的信息填空： （1）銷售價是110元的這一天，凈賺了_______元； （2）賣

6、完100件衣服后，他共凈賺了_________元； （3）如果不次再賣這種衣服100件，最好售價定為多少元，賣完100件衣服賺錢最多？說明你的理由． ★ 13． 9 100名兒童的智商(IQ)測試結(jié)果如下: IQ 70－79 80－89 90－99 100－109 110－119 120－129 130－139 140－149 人數(shù) 2 7 25 34 22 6 3 1 （1）畫出頻數(shù)分布宣方圖． （2）利用頻數(shù)分布直方圖求中位數(shù)（精確到0.1） ★ 13．10 甲、乙兩人在相同條件下各射靶10 次，每

7、次射耙的成績情況如圖 所示： （1）請?zhí)顚懴卤恚? 平均數(shù) 方差 中位數(shù) 命中9環(huán)以上次數(shù) 甲 7 1.2 乙 5.4 （2）請從下列四個不同角度對這次測試結(jié)果進(jìn)行分析： ①從平均數(shù)和方差相結(jié)合看； ②從平均數(shù)和中位數(shù)相結(jié)合看（分析誰的成績好些）； ③從平均數(shù)和命中9環(huán)以上次數(shù)相結(jié)合看分析誰的成績好些）； ④從折線上兩人射擊命中環(huán)數(shù)的走勢看（分析誰更有潛力）． ★13．11 甲、乙兩班舉行電腦漢字輸人速度比賽，各選10名學(xué)生參加，各班參賽學(xué)生每分鐘輸入漢字個數(shù)統(tǒng)計見下表． 輸入漢字/個 132 133

8、134 135 136 137 眾數(shù) 中位數(shù) 平均數(shù) 方差 甲班學(xué)生/人 1 0 1 5 2 1 135 135 135 1.6 乙班學(xué)生/人 0 1 4 1 2 2 請你填寫上表中乙班學(xué)生的相關(guān)數(shù)據(jù)，再根據(jù)所學(xué)的統(tǒng)計學(xué)知識，從不同方面評價甲、乙兩班學(xué)生的比賽成績(至少從兩個方面進(jìn)行評價）． ★★13．12 已知一組數(shù)據(jù)的方差為s2，將這組數(shù)據(jù)中的每一個數(shù)據(jù)都乘以k. 證明：所得到的一組新數(shù)據(jù)的方差是k2s2 ★★★13．13 將最小的31個自然數(shù)分成A、B兩組，10 在A組中，如果把10從A組移到B組中，則A組中各

9、數(shù)的算術(shù)平均數(shù)增加，B組中各數(shù)的算術(shù)平均數(shù)也增加．問：A組中原有多少個數(shù)? ★★★13．14 某次競賽共有15道題，下表是對于做對n (n＝0， 1， 2，…，15)道題的人數(shù)的一個統(tǒng)計，如果又知其中做對4道題和4道題以上的學(xué)生每人平均做對6道題，做對10道題和10道題以下的學(xué)生每人平均做對4道題，問：這個表至少統(tǒng)計了多少人？ n/道 0 1 2 3 … 12 13 14 15 做對n道題的人數(shù)/人 7 8 10 21 … 15 6 3 1 ★ 13．15 用An表示1， 2，…，101中能被n整除的所有數(shù)的算術(shù)平均數(shù)．問：A2、A3、A4、A5

10、、A6中最大的是哪一個？ ★★13．16 立方體每個頂點(diǎn)處都寫有一個數(shù)．除掉某一個頂點(diǎn)數(shù)以外，它們中每個數(shù)都比它鄰數(shù)的算術(shù)平均值要大1 (所謂鄰數(shù)就是指與它有棱相連的數(shù)）．那么剩下的那個頂點(diǎn)數(shù)與它鄰數(shù)算術(shù)平均值的差是多少呢？ ★★13. 17 將21個整數(shù)：-10，-9，-8，…，-3，-2，-1，0，1，2，3，…，8，9，10分為個數(shù)互不相等的6組數(shù)，分別計算各組的平均值，那么這6個平均值的和最大是多少? ★13.18 右圖是某一周蒙古貨幣圖格里克的外匯行情表，它表示各天每一圖格里克能兌換多少盧布(俄羅斯貨幣).彼得有30盧布，在該周某一天他把所有盧布換成了圖格里古，后來的某一天他又把全部圖格里克換成了盧布.這以后他再一次把所有盧布換成圖格里克，最后又把所有圖格里克換成盧布，到星期天他已有了54盧布.請寫出他在哪幾天進(jìn)行這交易. ★★13. 19 華羅庚爺爺在一首詩文中勉勵青少年： “猛攻苦戰(zhàn)是第一， 熟練生出百巧來， 勤能補(bǔ)拙是良訓(xùn)， 一分辛勞一分才.” 現(xiàn)在將詩文中不同的漢字對應(yīng)不同的自然數(shù)，相同的漢字對應(yīng)相同的自然數(shù)，并且不同漢字所對應(yīng)的自然數(shù)可以排列成一串連續(xù)的自然數(shù).如果這28個自然數(shù)的平均值是23，問：“分”字對應(yīng)的自然數(shù)的最大可能值是多少? 6