《高考數(shù)學(xué)一輪復(fù)習(xí)單元測(cè)試卷(13)-數(shù)形結(jié)合思想 大綱人教版(通用)》由會(huì)員分享�,可在線閱讀,更多相關(guān)《高考數(shù)學(xué)一輪復(fù)習(xí)單元測(cè)試卷(13)-數(shù)形結(jié)合思想 大綱人教版(通用)(13頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索�。
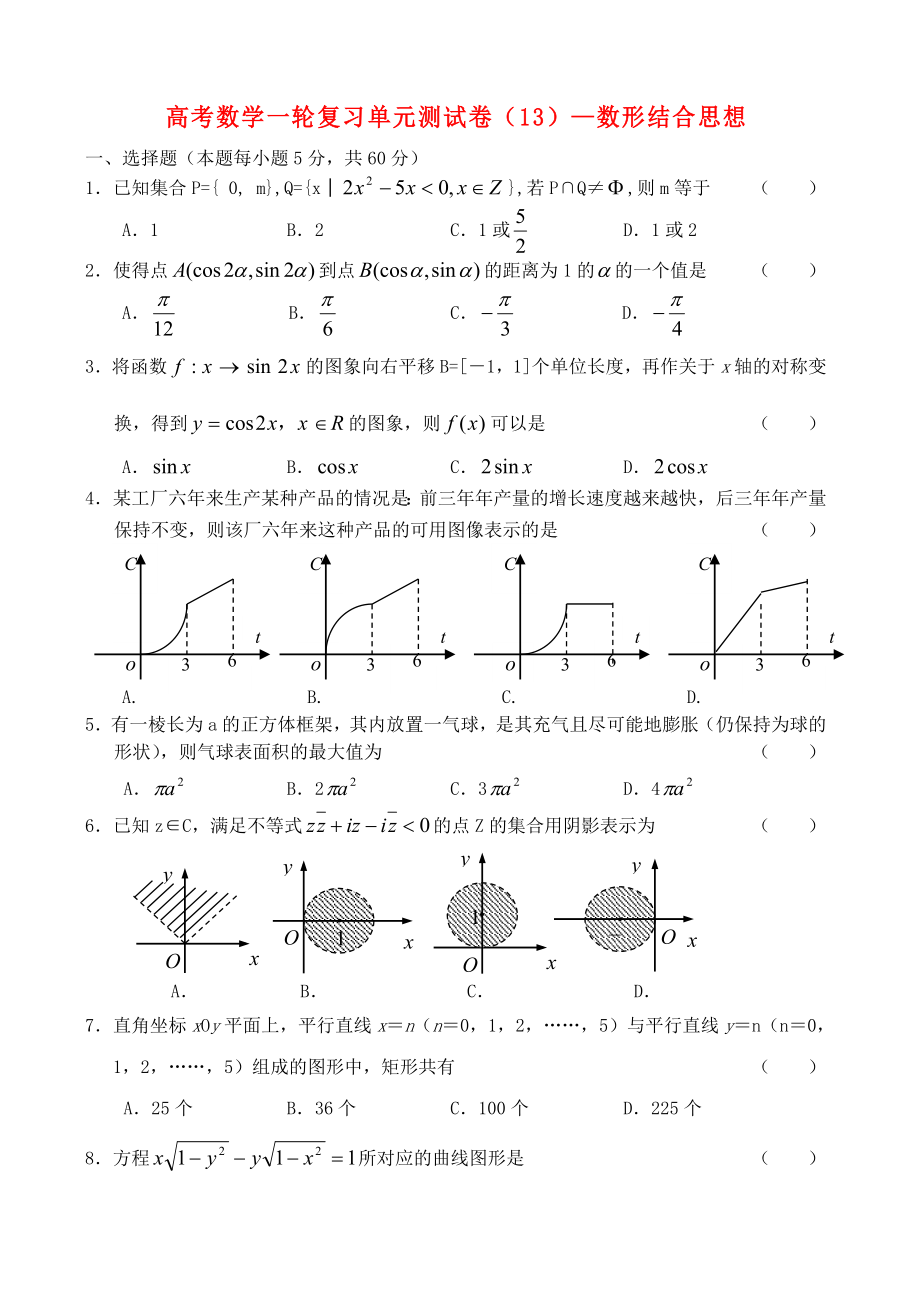
1、高考數(shù)學(xué)一輪復(fù)習(xí)單元測(cè)試卷(13)數(shù)形結(jié)合思想一�、選擇題(本題每小題5分,共60分)1已知集合P= 0, m,Q=x,若PQ,則m等于 ( )A1 B2 C1或 D1或22使得點(diǎn)到點(diǎn)的距離為1的的一個(gè)值是 ( )ABCD3將函數(shù)的圖象向右平移B=1�,1個(gè)單位長(zhǎng)度,再作關(guān)于x軸的對(duì)稱變換�,得到的圖象,則可以是 ( ) A B C D36Cot36Cot36Cot36Cot4某工廠六年來(lái)生產(chǎn)某種產(chǎn)品的情況是:前三年年產(chǎn)量的增長(zhǎng)速度越來(lái)越快�,后三年年產(chǎn)量保持不變�,則該廠六年來(lái)這種產(chǎn)品的可用圖像表示的是 ( )A. B. C. D.5有一棱長(zhǎng)為a的正方體框架,其內(nèi)放置一氣球�,是其充氣且盡可能地膨脹(仍
2、保持為球的形狀)�,則氣球表面積的最大值為 ( )A B2 C3 D4xyOxyO1xyO1xyO16已知zC�,滿足不等式的點(diǎn)Z的集合用陰影表示為 ( )A B C D7直角坐標(biāo)xOy平面上,平行直線xn(n0�,1,2�,5)與平行直線yn(n0, 1�,2,5)組成的圖形中�,矩形共有 ( )A25個(gè) B36個(gè)C100個(gè) D225個(gè)8方程所對(duì)應(yīng)的曲線圖形是( ) A B C D9設(shè)0x,則函數(shù)的最小值是 ( )A3 B2 CD2-10四面體的六條棱中�,其中五條棱的長(zhǎng)度都是2,則第六條棱長(zhǎng)的取值范圍是( ) A B C D11若直線與曲線有兩個(gè)不同的交點(diǎn)�,則的取值范圍是 ( )A BC D或12某企業(yè)
3、購(gòu)置了一批設(shè)備投入生產(chǎn)�,據(jù)分析每臺(tái)設(shè)備生產(chǎn)的總利潤(rùn)(單位:萬(wàn)元)與年數(shù)滿足如圖的二次函數(shù)關(guān)系。要使生產(chǎn)的年平均利潤(rùn)最大�,則每臺(tái)設(shè)備應(yīng)使用 ( )A3年 B4年 C5年 D6年二、填空題(本題每小題4分�,共16分)13若復(fù)數(shù)z滿足的最小值是_.14已知偶函數(shù)的圖象與軸有五個(gè)公共點(diǎn),那么方程的所有實(shí)根之和為_(kāi).15若z=滿足約束條件�,則Z的最大值和最小值分別為 16某池塘中野生水葫蘆的面積與時(shí)間的函數(shù)關(guān)系的圖象,如右圖所示. 假設(shè)其關(guān)系為指數(shù)函數(shù)�,并給出下列說(shuō)法此指數(shù)函數(shù)的底數(shù)為2;在第5個(gè)月時(shí)�,野生水葫蘆的面積就會(huì)超過(guò)30m2;野生水葫蘆從4m2蔓延到12m2只需1.5個(gè)月�;設(shè)野生水葫蘆蔓延到2
4、m2,3m2, 6m2所需的時(shí)間分別為t1, t2, t3, 則有t1 + t2 = t3�;野生水葫蘆在第1到第3個(gè)月之間蔓延的平均速度等于在第2到第4個(gè)月之間蔓延的平均速度.其中正確的說(shuō)法有 . (請(qǐng)把正確說(shuō)法的序號(hào)都填在橫線上)三、解答題(本大題共6小題�,共74分。解答應(yīng)寫出文字說(shuō)明�,證明過(guò)程或演算步驟):17(本小題滿分12分)已知函數(shù)的圖象向右平移個(gè)單位得到函數(shù)的圖象. (I)求函數(shù)g(x)的表達(dá)式; (II)證明當(dāng)時(shí),經(jīng)過(guò)函數(shù)g(x)圖象上任意兩點(diǎn)的直線的斜率恒大于零.18(本小題滿分12分)如圖所示�,已知四面體OABC中, M 為BC的中點(diǎn)�,N為AC的中點(diǎn),Q為OB的中點(diǎn)�,P為OA
5、的中點(diǎn)�,若AB=OC,試用向量方法證明�,PMQN.19(本小題滿分12分)為了能更好地了解鯨的生活習(xí)性,某動(dòng)物研究所在受傷的鯨身上安裝了電子監(jiān)測(cè)裝置�,從海岸放歸點(diǎn)A處(如圖所示)把它放歸大海�,并沿海岸線由西到東不停地對(duì)鯨進(jìn)行了40分鐘的跟蹤觀測(cè)�,每隔10分鐘踩點(diǎn)測(cè)得數(shù)據(jù)如下表(設(shè)鯨沿海面游動(dòng))。然后又在觀測(cè)站B處對(duì)鯨進(jìn)行生活習(xí)性的詳細(xì)觀測(cè)�。已知AB=15km�,觀測(cè)站B的觀測(cè)半徑為5km.觀測(cè)時(shí)刻t(分鐘)跟蹤觀測(cè)點(diǎn)到放歸點(diǎn)距離a(km)鯨位于跟蹤觀測(cè)點(diǎn)正北方向的距離b(km)10112023034042 (I)根據(jù)表中數(shù)據(jù):(1)計(jì)算鯨沿海岸線方向運(yùn)動(dòng)的速度,(2)寫出a�、b滿足的關(guān)系式并畫出
6�、鯨的運(yùn)動(dòng)路線簡(jiǎn)圖; (II)若鯨繼續(xù)以(I)(2)中的運(yùn)行路線運(yùn)動(dòng)�,則鯨經(jīng)過(guò)多少分鐘(從放歸時(shí)計(jì)時(shí))�,可進(jìn)入前方觀測(cè)站B的觀測(cè)范圍。20(本小題滿分12分)如圖所示�,已知圓為圓上一動(dòng)點(diǎn),點(diǎn)P在AM上�,點(diǎn)N在CM上�,且滿足的軌跡為 曲線E. (I)求曲線E的方程�; (II)若過(guò)定點(diǎn)F(0�,2)的直線交曲線E于不同的兩點(diǎn)G、H(點(diǎn)G在點(diǎn)F�、H之間), 且滿足�,求的取值范圍. 21(本小題滿分12分)在平面上有一系列點(diǎn)對(duì)每個(gè)自然數(shù),點(diǎn)位于函數(shù)的圖象上以點(diǎn)為圓心的與軸都相切,且與又彼此外切若,且 ()求證:數(shù)列是等差數(shù)列�; PnPn+1 ()設(shè)的面積為,, 求證:22(本小題滿分14分)已知a1�,數(shù)列
7、的通項(xiàng)公式是�,前n項(xiàng)和記作(n1,2�,)�,規(guī)定函數(shù)在處和每個(gè)區(qū)間(,)(i0�,1,2�,)上有定義,且,(i1�,2,)當(dāng)(�,)時(shí),f(x)的圖像完全落在連結(jié)點(diǎn)(�,)與點(diǎn)(,)的線段上 ()求f(x)的定義域�; ()設(shè)f(x)的圖像與坐標(biāo)軸及直線l:(n1,2�,)圍成的圖形面積為, 求及�; ()若存在正整數(shù)n�,使得,求a的取值范圍答案一�、選擇題(每小題5分,共60分):(1).D (2).C(3).C (4).A(5).B(6).C (7).D (8).D (9).C (10).B (11).A (12).C二�、填空題(每小題4分�,共16分)(13).1 ; (14).0�; (15). 17和11
8�、 �;(16). 三�、解答題(共74分�,按步驟得分)17. 解:(I)3分6分(II)證明一:依題意�,只需證明函數(shù)g(x)當(dāng)時(shí)是增函數(shù)在即的每一個(gè)區(qū)間上是增函數(shù)9分當(dāng)時(shí)�,在是增函數(shù)10分則當(dāng)時(shí)�,經(jīng)過(guò)函數(shù)g(x)圖像上任意兩點(diǎn)的直線的斜率恒大于零�。12分證明二:設(shè)函數(shù)g(x)圖像上任意兩點(diǎn)不妨設(shè)11分則當(dāng)時(shí)�,經(jīng)過(guò)函數(shù)g(x)圖像上任意兩點(diǎn)的直線的斜率恒大于零�。18. 證明 M是BC的中點(diǎn)�,連結(jié)OM�, =(+)。同理由N是AC的中點(diǎn)�,得=(+)�。=+=(+) =(+)=(+)�,=+=(+)=(+)=(+)=()�。=(+)()=()。|=|�,=0,即PMQN�。19.解:(I)由表中數(shù)據(jù)知(1)鯨沿海岸
9�、線方向運(yùn)行的速度為(km/分鐘)�。(2)a�、b滿足的關(guān)系式為。鯨的運(yùn)動(dòng)路線圖為(II)以點(diǎn)A為坐標(biāo)原點(diǎn)�,海岸線AB為x軸,建立直角坐標(biāo)系�,如圖�,設(shè)鯨所在的位置為點(diǎn)P(x,y)�,由(I)知�。又B(15�,0)�,依題意知,觀測(cè)站B的觀測(cè)區(qū)域?yàn)?,又�,即?�。故鯨從A點(diǎn)進(jìn)入前方觀測(cè)站B所用的時(shí)間為分鐘。答:鯨大約經(jīng)過(guò)113分鐘進(jìn)入B站的觀測(cè)范圍�。20. 解:(I) NP為AM的垂直平分線�,|NA|=|NM|.又動(dòng)點(diǎn)N的軌跡是以點(diǎn)C(1,0),A(1�,0)為焦點(diǎn)的橢圓.且橢圓長(zhǎng)軸長(zhǎng)為焦距2c=2. 曲線E的方程為(II)當(dāng)直線GH斜率存在時(shí),設(shè)直線GH方程為得設(shè)�,又當(dāng)直線GH斜率不存在�,方程為21. 解:(1)依題意�,的半徑,與彼此外切�, 兩邊平方�,化簡(jiǎn)得 , 即 , �, �, 數(shù)列是等差數(shù)列 (2) 由題設(shè)�,即�, �, 22. 解:(1)f(x)的定義域是�,由于所有的都是正數(shù)�,故是單調(diào)遞增的 f(x)的定義域是()(i1,2,)與i無(wú)關(guān)所有的,共線�,該直線過(guò)點(diǎn)(a,a)�,斜率為1-a,當(dāng)n2時(shí)�,是一個(gè)三角形與一個(gè)梯形面積之和(如上圖所示)梯形面積是于是 故 ()解法一:結(jié)合圖像�,易見(jiàn)即a2時(shí)�,而�,即a2時(shí)�,故當(dāng)1a2時(shí),存在正整數(shù)n�,使得解法二:假設(shè)存在正整數(shù)n�,使得,則應(yīng)有�,1a2時(shí)�,存在正整數(shù)n�,使得成立
 高考數(shù)學(xué)一輪復(fù)習(xí)單元測(cè)試卷(13)-數(shù)形結(jié)合思想 大綱人教版(通用)
高考數(shù)學(xué)一輪復(fù)習(xí)單元測(cè)試卷(13)-數(shù)形結(jié)合思想 大綱人教版(通用)