2014-2015學年高中數(shù)學（蘇教版必修二） 第一章立體幾何初步 第1章 章末總結(jié) 課時作業(yè)（含答案）

《2014-2015學年高中數(shù)學（蘇教版必修二） 第一章立體幾何初步 第1章 章末總結(jié) 課時作業(yè)（含答案）》由會員分享，可在線閱讀，更多相關(guān)《2014-2015學年高中數(shù)學（蘇教版必修二） 第一章立體幾何初步 第1章 章末總結(jié) 課時作業(yè)（含答案）（7頁珍藏版）》請在裝配圖網(wǎng)上搜索。

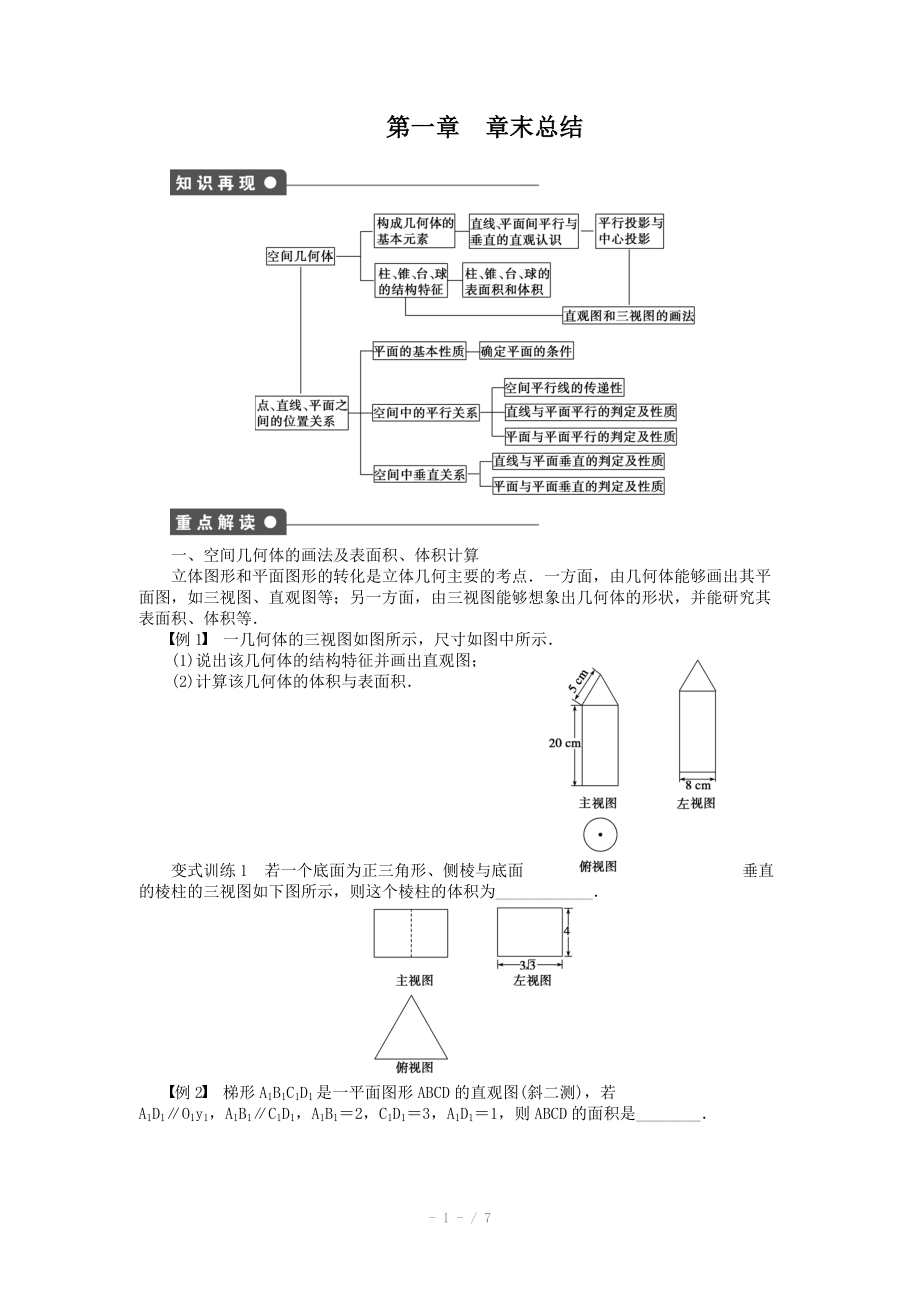
1、 第一章 章末總結(jié) 一、空間幾何體的畫法及表面積、體積計算 立體圖形和平面圖形的轉(zhuǎn)化是立體幾何主要的考點．一方面，由幾何體能夠畫出其平面圖，如三視圖、直觀圖等；另一方面，由三視圖能夠想象出幾何體的形狀，并能研究其表面積、體積等． 例1　一幾何體的三視圖如圖所示，尺寸如圖中所示． (1)說出該幾何體的結(jié)構(gòu)特征并畫出直觀圖； (2)計算該幾何體的體積與表面積． 變式訓練1　若一個底面為正三角形、側(cè)棱與底面垂直的棱柱的三視圖如下圖所示，則這個棱柱的體積為____________． 例2　梯形A1B1C1D1是一平面圖形A

2、BCD的直觀圖(斜二測)，若A1D1∥O1y1，A1B1∥C1D1，A1B1＝2，C1D1＝3，A1D1＝1，則ABCD的面積是________． - 1 - / 7 變式訓練2　等腰梯形ABCD，上底CD＝1，腰AD＝CB＝，下底AB＝3，以下底所在直線為x軸，則由斜二測畫法畫出的直觀圖A′B′C′D′的面積為______． 二、平面基本性質(zhì)的應(yīng)用 1．關(guān)于多點共線問題往往需證明這些點在某兩個平面的交線上． 2．多線共點問題的證明往往讓其他線都過某兩條線的交點． 3．多點共面問題的證明往往讓其他點在某三點或四點確定的平面上． 4．多線共面問題的證明往往讓其他線在某兩條直

3、線確定的平面內(nèi)． 例3　如圖所示，空間四邊形ABCD中，E，F(xiàn)分別為AB，AD的中點，G，H分別在BC，CD上，且BG∶GC＝DH∶HC＝1∶2． 求證：(1)E、F、G、H四點共面； (2)GE與HF的交點在直線AC上． 變式訓練3　如圖，四邊形ABB′A′，BCC′B′，CAA′C′都是梯形．求證：三直線AA′，BB′，CC′相交于一點． 三、直線、平面的位置關(guān)系 1．空間平行關(guān)系的判定方法： (1)判定線線平行的方法． ①利用線線平行的定義證共面而且無公共點(結(jié)合反證法)； ②利用平行公理4

4、； ③利用線面平行性質(zhì)定理； ④利用線面垂直的性質(zhì)定理(若a⊥α，b⊥α，則a∥b)； ⑤利用面面平行性質(zhì)定理(若α∥β，α∩γ＝a，β∩γ＝b，則a∥b)． (2)判斷線面平行的方法： ①線面平行的定義(無公共點)； ②利用線面平行的判定定理(a?α，b?α，a∥b?a∥α)； ③面面平行的性質(zhì)定理(α∥β，a?α?a∥β)； ④面面平行的性質(zhì)(α∥β，a?α，a?β，a∥α?a∥β)． (3)面面平行的判定方法有： ①平面平行的定義(無公共點)； ②判定定理(若a∥β，b∥β，a、b?α，且a∩b＝A，則α∥β)； ③判定定理的推論(若a∥a′，b∥b′，a

5、?α，b?α且a∩b＝A，a′?β，b′?β，且a′∩b′＝A′，則α∥β)； ④線面垂直性質(zhì)定理(若a⊥α，a⊥β，則α∥β)； ⑤平面平行的性質(zhì)(傳遞性：α∥β，β∥γ?α∥γ)． 平行關(guān)系的轉(zhuǎn)化是： 2．空間垂直關(guān)系的判定方法： (1)判定線線垂直的方法有： ①計算所成的角為90(包括平面角和異面直線所成的角)； ②線面垂直的性質(zhì)(若a⊥α，b?α，則a⊥b)； ③面面垂直的定義：若兩平面垂直，則兩平面相交形成的二面角的平面角為90． (2)判定線面垂直的方法有： ①線面垂直定義(一般不易驗證任意性)； ②線面垂直的判定定理(a⊥b，a⊥c，b?α，c?α，b∩

6、c＝M?a⊥α)； ③平行線垂直平面的傳遞性質(zhì)(a∥b，b⊥α?a⊥α)； ④面面垂直的性質(zhì)(α⊥β，α∩β＝l，a?β，a⊥l?a⊥α)； ⑤面面平行的性質(zhì)(a⊥α，α∥β?a⊥β)； ⑥面面垂直的性質(zhì)(α∩β＝l，α⊥γ，β⊥γ?l⊥γ)． (3)面面垂直的判定方法有： ①根據(jù)定義(作兩平面構(gòu)成二面角的平面角，計算其為90)； ②面面垂直的判定定理(a⊥β，a?α?α⊥β)． 垂直關(guān)系的轉(zhuǎn)化是： 例4　如圖所示，在四棱錐P—ABCD中，側(cè)面PAD是正三角形，且與底面ABCD垂直，底面ABCD是邊長為2的菱形，∠BAD＝60，N是PB的中點，過A，D，N的平面交PC于M

7、，E為AD的中點．求證： (1)EN∥平面PDC； (2)BC⊥平面PEB； (3)平面PBC⊥平面ADMN． 變式訓練4　如圖所示，在四棱錐P—ABCD中，底面ABCD是正方形，側(cè)棱PD⊥底面ABCD，PD＝DC，E是PC的中點，過E點作EF⊥PB交PB于點F．求證： (1)PA∥平面EDB； (2)PB⊥平面EFD． 第一章 章末總結(jié) 答案 例1　 解　(1)由三視圖知該幾何體是由一個圓柱與一個等底圓錐拼接而成的組合體，其直觀圖如圖所示． (2)由三視圖中尺寸知，組合體下

8、部是底面直徑為8 cm，高為20 cm的圓柱，上部為底面直徑為8 cm，母線長為5 cm的圓錐． 易求得圓錐高h＝＝3(cm)， ∴體積V＝π4220＋π423＝336π(cm3)， 表面積S＝π42＋2π420＋π45 ＝196π(cm2)． ∴該幾何體的體積為336π cm3，表面積為196π cm2． 點評　三視圖畫法：它包括主視圖、左視圖、俯視圖三種．畫圖時要遵循“高平齊、長對正、寬相等”的原則，同時還要注意被擋住的輪廓線畫成虛線． 變式訓練1　36 解析　觀察三視圖得棱柱底面正三角形的高和側(cè)棱長．注意圖中數(shù)據(jù)3是底面正三角形的高，不是邊長． 棱柱的側(cè)棱長為4，底面正

9、三角形的高為3，設(shè)邊長為a，則a＝3，所以a＝6．所以底面積為a2＝9．所以棱柱的體積為94＝36． 例2　5 解析　把圖還原，ABCD為直角梯形，AB＝A1B1＝2，CD＝C1D1＝3，AD＝2A1D1＝2． ∴S梯ABCD＝＝5． 點評　斜二測畫法：主要用于水平放置的平面圖畫法或立體圖形的畫法．它的主要步驟：①畫軸；②畫平行于x，y，z軸的線段分別為平行于x′，y′，z′軸的線段；③截線段，平行于x，z軸的線段的長度不變，平行于y軸的線段的長度變?yōu)樵瓉淼囊话耄? 變式訓練2　 解析　 ∵OE＝＝1，∴O′E′＝，E′F＝， ∴直觀圖A′B′C′D′的面積為

10、S′＝(1＋3)＝． 例3　證明　(1)∵BG∶GC＝DH∶HC， ∴GH∥BD，又EF∥BD，∴EF∥GH， ∴E、F、G、H四點共面． (2)∵G，H不是BC、CD的中點，∴EF≠GH． 又EF∥GH， ∴EG與FH不平行，則必相交，設(shè)交點為M． ?M∈面ABC且M∈面ACD ?M在面ABC與面ACD的交線上 ?M∈AC． ∴GE與HF的交點在直線AC上． 點評　證明線共點、點共線、線共面問題，重要是應(yīng)用平面的基本性質(zhì)，先證部分元素共點、共線、共面，再利用公理1,2,3證明其他元素也具有這個性質(zhì)，要熟練地掌握這三個公理． 變式訓練3　證明　梯形ABB′A′中，A′B

11、′∥AB． ∴AA′，BB′在同一平面A′B內(nèi)． 設(shè)直線AA′，BB′相交于點P， 同理BB′、CC′同在平面BC′內(nèi)，CC′、AA′同在平面A′C內(nèi)． ∵P∈AA′，AA′?平面A′C， ∴P∈平面A′C． 同理點P∈平面BC′． 根據(jù)公理2，點P在平面A′C與平面BC′的交線上，而平面A′C∩平面BC′＝CC′，故點P ∈直線CC′，即三直線AA′、BB′、CC′相交于一點． 例4　證明　(1)因為AD∥BC，BC?平面PBC， AD?平面PBC，所以AD∥平面PBC， 又平面ADMN∩平面PBC＝MN， 所以AD∥MN，所以MN∥BC． 因為N為PB的

12、中點，所以M為PC的中點， 所以MN∥BC，且MN＝BC． 又E為AD的中點， 所以四邊形DENM為平行四邊形． 所以EN∥DM． 又EN?平面PDC，DM?平面PDC， 所以EN∥平面PDC． (2)因為ABCD為邊長為2的菱形，且∠BAD＝60， 所以BE⊥AD．又因為PE⊥AD，PE∩BE＝E， 所以AD⊥平面PEB． 因為AD∥BC，所以BC⊥平面PEB． (3)由(2)知AD⊥PB． 又因為PA＝AB且N為PB的中點， 所以AN⊥PB，又AD∩AN＝A， 所以PB⊥平面ADMN． 又PB?平面PBC，所以平面PBC⊥平面ADMN． 點評　立體幾何的證明

13、，我們要牢牢抓住“轉(zhuǎn)化”這一思想，線與線，線與面，面與面之間的垂直與平行都可互相轉(zhuǎn)化，轉(zhuǎn)化的理論依據(jù)是這三種平行與垂直的判定定理、性質(zhì)定理等． 變式訓練4　證明　(1)如圖所示，連結(jié)AC交BD于O，連結(jié)EO． ∵底面ABCD是正方形， ∴點O是AC的中點． 在△PAC中，EO是中位線， ∴PA∥EO． 而EO?平面EDB且PA?平面EDB， ∴PA∥平面EDB． (2)∵PD⊥底面ABCD，且DC?平面ABCD， ∴PD⊥DC．∵PD＝DC， ∴△PDC是等腰直角三角形． 又DE是斜邊PC的中線，∴DE⊥PC． ① 由PD⊥底面ABCD，得PD⊥BC． ∵底面ABCD是正方形，∴DC⊥BC． ∴BC⊥平面PDC． 又DE?平面PDC，∴BC⊥DE． ② 由①和②推得DE⊥平面PBC． 而PB?平面PBC，∴DE⊥PB． 又EF⊥PB，且DE∩EF＝E， ∴PB⊥平面EFD． 希望對大家有所幫助，多謝您的瀏覽！