新編高考數(shù)學(xué)浙江理科一輪【第八章】立體幾何 第2講空間幾何體的表面積與體積

《新編高考數(shù)學(xué)浙江理科一輪【第八章】立體幾何 第2講空間幾何體的表面積與體積》由會(huì)員分享，可在線(xiàn)閱讀，更多相關(guān)《新編高考數(shù)學(xué)浙江理科一輪【第八章】立體幾何 第2講空間幾何體的表面積與體積（7頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

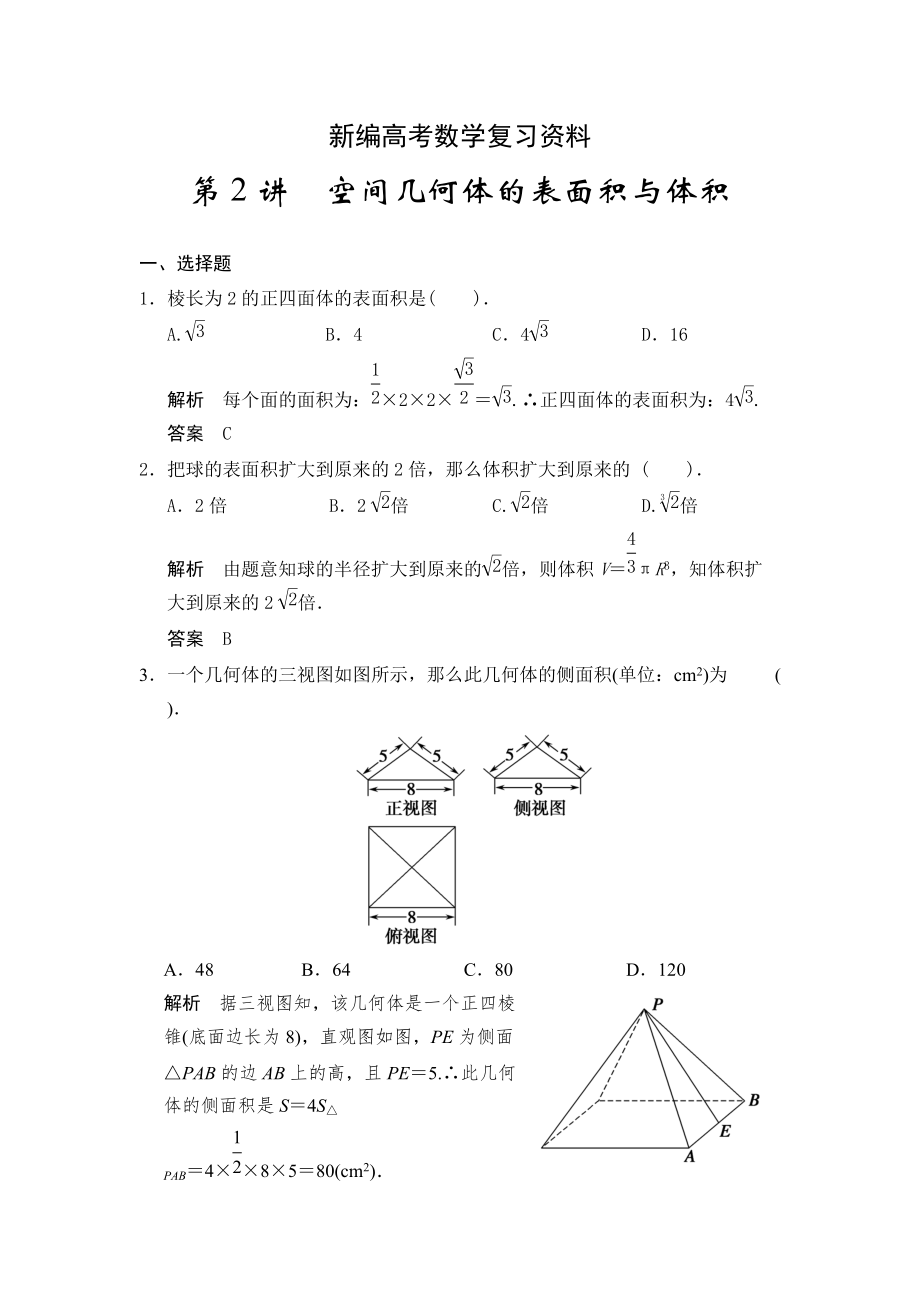
1、新編高考數(shù)學(xué)復(fù)習(xí)資料 第2講 空間幾何體的表面積與體積 一、選擇題 1．棱長(zhǎng)為2的正四面體的表面積是(　　)． A. B．4 C．4 D．16 解析　每個(gè)面的面積為：×2×2×＝.∴正四面體的表面積為：4. 答案　C 2．把球的表面積擴(kuò)大到原來(lái)的2倍，那么體積擴(kuò)大到原來(lái)的 (　　)． A．2倍 B．2倍 C.倍 D.倍 解析　由題意知球的半徑擴(kuò)大到原來(lái)的倍，則體積V＝πR3，知體積擴(kuò)大到原來(lái)的2倍． 答案　B 3．一個(gè)幾何體的三視圖如圖所示，那么此幾

2、何體的側(cè)面積(單位：cm2)為 (　　)． A．48 B．64 C．80 D．120 解析　據(jù)三視圖知，該幾何體是一個(gè)正四棱錐(底面邊長(zhǎng)為8)，直觀圖如圖，PE為側(cè)面△PAB的邊AB上的高，且PE＝5.∴此幾何體的側(cè)面積是S＝4S△PAB＝4××8×5＝80(cm2)． 答案　C 4．已知三棱錐S－ABC的所有頂點(diǎn)都在球O的球面上，△ABC是邊長(zhǎng)為1的正三角形，SC為球O的直徑，且SC＝2，則此棱錐的體積為 (　　)． A. B. C. D. 解析　在直角三角形ASC中，AC＝1，∠SAC＝90°，SC＝2，∴SA＝＝；同理S

3、B＝.過(guò)A點(diǎn)作SC的垂線(xiàn)交SC于D點(diǎn)，連接DB，因△SAC≌△SBC，故BD⊥SC，故SC⊥平面ABD，且平面ABD為等腰三角形，因∠ASC＝30°，故AD＝SA＝，則△ABD的面積為×1× ＝，則三棱錐的體積為××2＝. 答案　A 5．某品牌香水瓶的三視圖如下(單位：cm)，則該幾何體的表面積為 (　　)． A.cm2 B.cm2 C.cm2 D.cm2 解析　該幾何體的上下為長(zhǎng)方體，中間為圓柱． S表面積＝S下長(zhǎng)方體＋S上長(zhǎng)方體＋S圓柱側(cè)－2S圓柱底＝2×4×4＋4×4×2＋2×3×3＋4×3×1＋2π××1－2

4、×π2＝94＋. 答案　C 6．已知球的直徑SC＝4，A，B是該球球面上的兩點(diǎn)，AB＝，∠ASC＝∠BSC＝30°，則棱錐S-ABC的體積為(　　)． A．3 B．2 C. D．1 解析　由題可知AB一定在與直徑SC垂直的小圓面上，作過(guò)AB的小圓交直徑SC于D，設(shè)SD＝x，則DC＝4－x，此時(shí)所求棱錐即分割成兩個(gè)棱錐S-ABD和C-ABD，在△SAD和△SBD中，由已知條件可得AD＝BD＝x，又因?yàn)镾C為直徑，所以∠SBC＝∠SAC＝90°，所以∠DCB＝∠DCA＝60°，在△BDC中 ，BD＝(4－x)，所以x＝(4－x)

5、，所以x＝3，AD＝BD＝，所以三角形ABD為正三角形，所以V＝S△ABD×4＝. 答案　C 二、填空題 7．已知S、A、B、C是球O表面上的點(diǎn)，SA⊥平面ABC，AB⊥BC，SA＝AB＝1，BC＝，則球O的表面積等于________． 解析　將三棱錐S－ABC補(bǔ)形成以SA、AB、BC為棱的長(zhǎng)方體，其對(duì)角線(xiàn)SC為球O的直徑，所以2R＝SC＝2，R＝1，∴表面積為4πR2＝4π. 答案　4π 8．如圖所示，已知一個(gè)多面體的平面展開(kāi)圖由一個(gè)邊長(zhǎng)為1的正方形和4個(gè)邊長(zhǎng)為1的正三角形組成，則該多面體的體積是________． 解析　由題知該多面體為正四棱錐，底面邊長(zhǎng)為1，側(cè)棱長(zhǎng)為1，

6、斜高為，連接頂點(diǎn)和底面中心即為高，可求得高為，所以體積V＝×1×1×＝. 答案　 9．已知某幾何體的直觀圖及三視圖如圖所示，三視圖的輪廓均為正方形，則該幾何體的表面積為_(kāi)_______． 解析　借助常見(jiàn)的正方體模型解決．由三視圖知，該幾何體由正方體沿面AB1D1與面CB1D1截去兩個(gè)角所得，其表面由兩個(gè)等邊三角形、四個(gè)直角三角形和一個(gè)正方形組成．計(jì)算得其表面積為12＋4. 答案　12＋4 10．如圖所示，正方體ABCD－A1B1C1D1的棱長(zhǎng)為6，則以正方體ABCD－A1B1C1D1的中心為頂點(diǎn)，以平面AB1D1截正方體外接球所得的圓為底面的圓錐的全面積為_(kāi)_______． 解

7、析　設(shè)O為正方體外接球的球心，則O也是正方體的中心，O到平面AB1D1的距離是體對(duì)角線(xiàn)長(zhǎng)的，即為.又球的半徑是正方體對(duì)角線(xiàn)長(zhǎng)的一半，即為3，由勾股定理可知，截面圓的半徑為＝2，圓錐底面面積為S1＝π·(2)2＝24π，圓錐的母線(xiàn)即為球的半徑3，圓錐的側(cè)面積為S2＝π×2×3＝18π.因此圓錐的全面積為S＝S2＋S1＝18π＋24π＝(18＋24)π. 答案　(18＋24)π 三、解答題 11 .一個(gè)幾何體的三視圖如圖所示．已知主視圖是底邊長(zhǎng)為1的平行四邊形，左視圖是一個(gè)長(zhǎng)為，寬為1的矩形，俯視圖為兩個(gè)邊長(zhǎng)為1的正方形拼成的矩形． (1)求該幾何體的體積V； (2)求該幾何體的表面積S

8、. 解 (1)由三視圖可知，該幾何體是一個(gè)平行六面體(如 圖)，其底面是邊長(zhǎng)為1的正方形，高為， 所以V＝1×1×＝. (2)由三視圖可知，該平行六面體中， A1D⊥平面ABCD，CD⊥平面BCC1B1， 所以AA1＝2，側(cè)面ABB1A1，CDD1C1均為矩形， S＝2×(1×1＋1×＋1×2)＝6＋2. 12．在直三棱柱ABC－A1B1C1中，底面為直角三角形，∠ACB＝90°，AC＝6，BC＝CC1＝，P是BC1上一動(dòng)點(diǎn)，如圖所示，求CP＋PA1的最小值． 解　PA1在平面A1BC1內(nèi)，PC在平面BCC1內(nèi)，將其鋪平后轉(zhuǎn)化為平面上的問(wèn)題解決．鋪

9、平平面A1BC1、平面BCC1，如圖所示．計(jì)算A1B＝AB1＝，BC1＝2，又A1C1＝6，故△A1BC1是∠A1C1B＝90°的直角三角形． CP＋PA1≥A1C.在△AC1C中，由余弦定理，得 A1C＝＝＝5， 故(CP＋PA1)min＝5. 13．某高速公路收費(fèi)站入口處的安全標(biāo)識(shí)墩如圖1所示，墩的上半部分是正四棱錐PEFGH，下半部分是長(zhǎng)方體ABCDEFGH.圖2、圖3分別是該標(biāo)識(shí)墩的主視圖和俯視圖． (1)請(qǐng)畫(huà)出該安全標(biāo)識(shí)墩的左視圖； (2)求該安全標(biāo)識(shí)墩的體積． 解　(1)左視圖同主視圖，如圖所示： (2)該安全標(biāo)識(shí)墩的體積為 V＝VPEFGH＋VABCDE

10、FGH ＝×402×60＋402×20 ＝64 000(cm3)． 14．如圖(a)，在直角梯形ABCD中，∠ADC＝90°，CD∥AB，AB＝4，AD＝CD＝2，將△ADC沿AC折起，使平面ADC⊥平面ABC，得到幾何體D－ABC，如圖(b)所示． (1)求證：BC⊥平面ACD； (2)求幾何體D－ABC的體積． (1)證明　在圖中，可得AC＝BC＝2， 從而AC2＋BC2＝AB2， 故AC⊥BC， 又平面ADC⊥平面ABC，平面ADC∩平面ABC＝AC，BC?平面ABC，∴BC⊥平面ACD. (2)解　由(1)可知，BC為三棱錐B－ACD的高，BC＝2，S△ACD＝2， ∴VB－ACD＝S△ACD·BC＝×2×2＝， 由等體積性可知，幾何體D－ABC的體積為.