七年級(jí)數(shù)學(xué)下學(xué)期第一次月考試題 人教新版

《七年級(jí)數(shù)學(xué)下學(xué)期第一次月考試題 人教新版》由會(huì)員分享，可在線(xiàn)閱讀，更多相關(guān)《七年級(jí)數(shù)學(xué)下學(xué)期第一次月考試題 人教新版（7頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

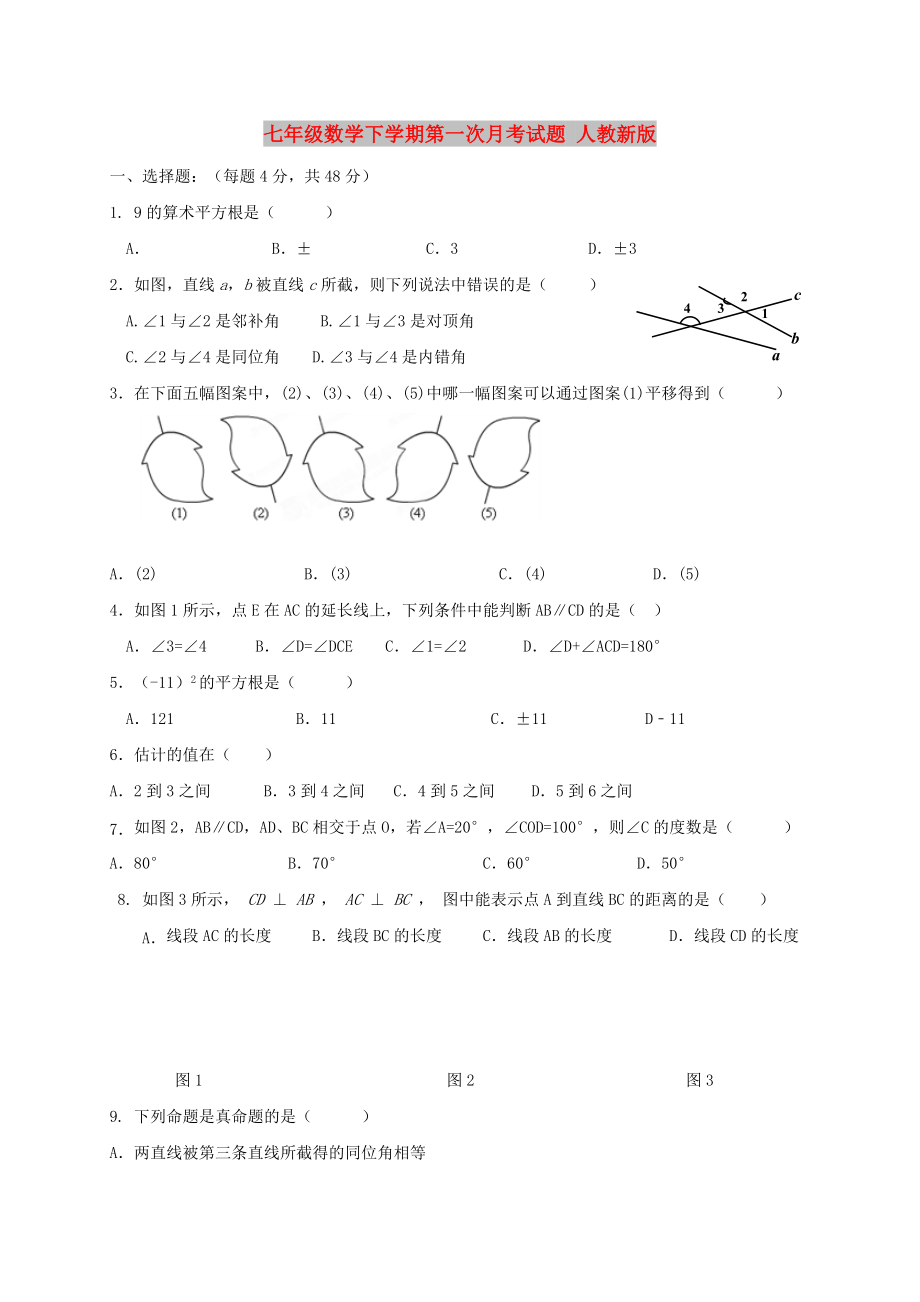
1、七年級(jí)數(shù)學(xué)下學(xué)期第一次月考試題 人教新版 一、選擇題：（每題4分，共48分） 1. 9的算術(shù)平方根是（ ） A． B．± C．3 D．±3 a b c 1 2 3 4 2．如圖，直線(xiàn)a，b被直線(xiàn)c所截，則下列說(shuō)法中錯(cuò)誤的是（ ） A.∠1與∠2是鄰補(bǔ)角 B.∠1與∠3是對(duì)頂角 C.∠2與∠4是同位角 D.∠3與∠4是內(nèi)錯(cuò)角 3．在下面五幅圖案中，(2)、(3)、(4)、(5)中哪一幅圖案可以通過(guò)圖案(1)平移得到（ ） A

2、．(2) B．(3) C．(4) D．(5) 4．如圖1所示，點(diǎn)E在AC的延長(zhǎng)線(xiàn)上，下列條件中能判斷AB∥CD的是（　） A．∠3=∠4 B．∠D=∠DCE C．∠1=∠2 D．∠D+∠ACD=180° 5．（-11）2的平方根是（ ） A．121 B．11 C．±11 D﹣11 6．估計(jì)的值在（　?。? A．2到3之間 B．3到4之間 C．4到5之間 D．5到

3、6之間 7． 如圖2，AB∥CD，AD、BC相交于點(diǎn)O，若∠A=20°，∠COD=100°，則∠C的度數(shù)是（ ） A．80° B．70° C．60° D．50° 8. 如圖3所示， CD ⊥ AB ， AC ⊥ BC ， 圖中能表示點(diǎn)A到直線(xiàn)BC的距離的是（　?。? A． 線(xiàn)段AC的長(zhǎng)度 ? B．線(xiàn)段BC的長(zhǎng)度 C．線(xiàn)段AB的長(zhǎng)度? D．線(xiàn)段CD的長(zhǎng)度 圖1 圖2

4、 圖3 9. 下列命題是真命題的是（ ?） A．兩直線(xiàn)被第三條直線(xiàn)所截得的同位角相等 B．兩直線(xiàn)被第三條直線(xiàn)所截得的同旁?xún)?nèi)角互補(bǔ) C．兩平行線(xiàn)被第三條直線(xiàn)所截得的同位角的平分線(xiàn)互相垂直 D．兩平行線(xiàn)被第三條直線(xiàn)所截得的同旁?xún)?nèi)角的平分線(xiàn)互相垂直 10.如圖，是用棋子擺成的“上”字：如果按照此規(guī)律繼續(xù)擺下去，那么通過(guò)觀察，可以發(fā)現(xiàn)：第10個(gè)“上”字需用多少枚棋子（ ） 圖① 圖② 圖③ A．36 B．38 C

5、．42 D．50 11． 將一張長(zhǎng)方形紙片沿EF折疊，折疊后的位置 如圖所示， 若∠EFB=65°，則∠AED′等于（ ） A．70° B．65° C．50° D．25° 12．如圖，AB∥EF，∠C=90°，則α、β、γ的關(guān)系是( ) A．β+γ﹣α=90° B． α+β﹣γ=90° C．α+β+γ=180° D．β=α+γ 二、填空題：（每題4分，共24分） 13． -8的立方根是 ；

6、 14．如圖4，把小河里的水引到田地A處就作AB，垂足為B，沿AB挖水溝，水溝最短．理由是： . 15．把命題“對(duì)頂角相等”寫(xiě)成“如果…那么…”的形式 為：__ . 16．已知滿(mǎn)足，則的值是 ； 17．若＝5.036，＝15.906，則＝__________. 18、如果∠α的兩邊分別平行于∠β的兩邊,且∠α比∠β的2倍少30°,則∠α,∠β的度數(shù)分別

7、是　 　.? 三、解答題:(本大題共2個(gè)小題，每小題8分，共16分) 19．計(jì)算（8分） (1) (2) 20．（8分）求下列各式中的值 (1) (2) 四、 解答題：(本大題共5個(gè)小題，每小題10分，共50分) 21.如圖，在邊長(zhǎng)為1的小正方形組成的網(wǎng)格中，△ABC的頂點(diǎn)均在格點(diǎn)上，請(qǐng)按要求完成下列各題： （1）平移△ABC，使得點(diǎn)A與點(diǎn)D 重合，在網(wǎng)格中作出平移后的△DEF. （2）求△DEF的面積. 22.若正數(shù)m的平方根是5a＋1和a－19，求m的值及m的

8、平方根. 23.完成下列推理說(shuō)明： 如圖，已知∠1 ＝∠2，∠B ＝∠C，可推得AB∥CD．理由如下： ∵∠1 ＝∠2（已知），且∠1 ＝∠CGD（______________ _________）， ∴∠2 ＝∠CGD（等量代換）． ∴CE∥BF（___________________ ________）． ∴∠ ＝∠C（__________________________）． 又∵∠B ＝∠C（已知），∴∠ ＝∠B（等量代換）． ∴AB∥CD（______________________________

9、__）． F 24. 已知：如圖，∠AEH＝130°，∠EFD＝50°，∠SMB＝120°． 求∠DNG的度數(shù)． 25. 如圖所示，已知∠1＋∠2＝180°，∠B＝∠3， （1） 求證：BD∥EF （2） 求證：∠AED＝∠ACB 五、解答題：(本大題共1個(gè)小題，共12分) 26．如圖，已知AB∥CD，CE，BE的交點(diǎn)為E，現(xiàn)作如下操作： 第一次操作，分別作∠ABE和∠DCE的平分線(xiàn)，交點(diǎn)為E1， 第二次操作，分別作∠ABE1和∠DCE1的平分線(xiàn)，交點(diǎn)為E2， 第三次操作，分別作∠ABE2和∠

10、DCE2的平分線(xiàn)，交點(diǎn)為E3…… 第n次操作，分別作∠ABEn－1和∠DCEn－1的平分線(xiàn)，交點(diǎn)為En. (1)如圖①，求證：∠E＝∠B＋∠C； (2)如圖②，求證：∠E1＝∠E； (3)猜想：若∠En＝b°，求∠BEC的度數(shù)． xx下期第一次月考初一數(shù)學(xué)試題 數(shù)學(xué)試題參考答案 一、 選擇題：CDBCC BCADC CB 二、 填空題： 13、 -2 14、垂線(xiàn)段最短 15、如果兩個(gè)角是對(duì)頂角，那么這兩個(gè)角相等 16、1 17、503.6

11、18、110°，70° 三、解答題： 19．(1)解：原式=5-1=4 ……3分 (2) 解：原式=-3-0- + + ……6分 = -2 ……8分 20． (1)解： (2)解：

12、 ……4分 ……8分 四、解答題： 21、（1）略 ……5分 （2）……10分 22、解：由題意得：5a＋1+ a－19=0 解得： a=3 ……5分 m=5a＋1=5×3+1=16 16的平方根是±4 ……10分 23.完成

13、下列推理說(shuō)明： 如圖，已知∠1 ＝∠2，∠B ＝∠C，可推得AB∥CD．理由如下： ∵∠1 ＝∠2（已知），且∠1 ＝∠CGD（對(duì)等角相等）， ∴∠2 ＝∠CGD（等量代換）． ∴CE∥BF（同位角相等，兩直線(xiàn)平行）． ∴∠BFD＝∠C（兩直線(xiàn)平行，同位角相等）． 又∵∠B ＝∠C（已知）， ∴∠BFD ＝∠B（等量代換 ）． ∴AB∥CD（內(nèi)錯(cuò)角相等，兩直線(xiàn)平行）． 24、解：∵∠AEH＝130°，∠EFD＝50° ∴∠MEF=∠AEH＝130° ∴∠MEF+∠EFD=130°+50°=180° ∴AB∥CD

14、 F F ∴∠MND=∠SMB＝120° F ∴∠DNG=180°-∠MND=180°-120°=60° ……10分 25. （1）∵∠1＋∠2＝180°，∠1＋∠4＝180°， ∴∠2＝∠4. ∴BD∥FE ……4分 （2）∵BD∥FE（已證） ∴∠3＝∠ADE. ∵∠3＝∠B， ∴∠B＝∠ADE. ∴DE∥BC. ∴∠AED＝∠ACB. ……10分 26. (1)證明：如圖，過(guò)E作EF∥AB. ∵AB∥CD，∴AB∥EF∥CD， ∴∠B＝∠1，∠C＝∠2. ∵∠BEC＝∠1＋∠2， ∴∠BEC＝∠B＋∠C.(4分) （2）證明：由(1)可得∠E1＝∠ABE1＋∠DCE1 ∵∠ABE和∠DCE的平分線(xiàn)交點(diǎn)為E1 ∴∠E1＝∠ABE＋∠DCE=(∠ABE+∠DCE) 又∵由（1）得∠E＝∠ABE＋∠DCE ∴∠E1＝∠E；(8分) (3)解：當(dāng)∠En＝b°時(shí)，∠BEC＝2nb°.(12分)