《內(nèi)蒙古滿洲里市第七中學高中數(shù)學 第二章平面向量《向量加法練習》課件 新人教A版必修4》由會員分享���,可在線閱讀��,更多相關(guān)《內(nèi)蒙古滿洲里市第七中學高中數(shù)學 第二章平面向量《向量加法練習》課件 新人教A版必修4(21頁珍藏版)》請在裝配圖網(wǎng)上搜索����。
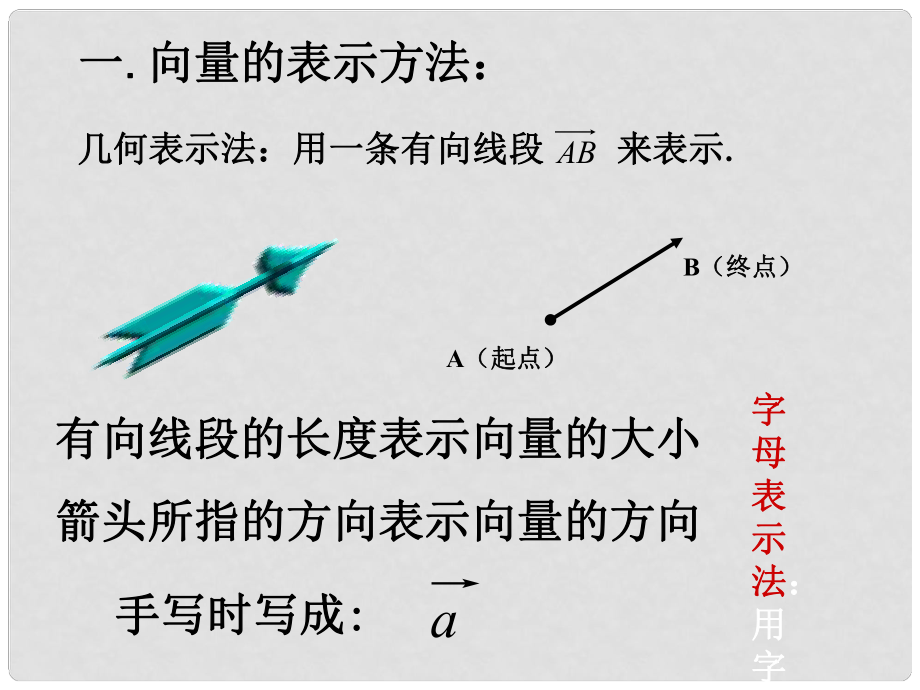
1�����、一一. .向量的表示方法向量的表示方法:手寫時寫成手寫時寫成: :a有向線段的長度表示向量的大小有向線段的長度表示向量的大小箭頭所指的方向表示向量的方向箭頭所指的方向表示向量的方向 幾何表示法:用一條有向線段幾何表示法:用一條有向線段 來表示來表示. .AB字字母母表表示示法法:用用字字母母a a、b b�����、c c( (黑黑體體字字) )或或 來來表表示示. .A BA(起點)(起點)B(終點)(終點)2 2���、單位向量:長度為單位向量:長度為 1 1 個單位長度的向量個單位長度的向量. .零向量模為零向量模為0 0�,方向不確定�,方向不確定. .單位向量模為單位向量模為1 1,方向不一定相同�����,方向
2�、不一定相同. .二二. .兩個特殊向量兩個特殊向量:思考:思考:平面直角坐標系內(nèi),起點在原點的單位向平面直角坐標系內(nèi)��,起點在原點的單位向量��,量����, 它們的終點的軌跡是什么圖形?它們的終點的軌跡是什么圖形?1 1�����、零向量:長度為�����、零向量:長度為 0 0 的向量的向量. . 記作記作 . .0O Oy yx x單位圓三三. .平行向量:平行向量:規(guī)定零向量與任一向量平行規(guī)定零向量與任一向量平行. .abab/記作:efef嗎與 是平行向量��?兩向量的平行與平面幾何里兩線段的平行有什么區(qū)別��?兩向量的平行與平面幾何里兩線段的平行有什么區(qū)別�����?方向相同或相反的非零向量叫做平行向量方向相同或相反的非零向量叫做平
3��、行向量. .任意一組平行向量都可以平移到同一直線上任意一組平行向量都可以平移到同一直線上四四. .共線向量:共線向量:平行向量又稱共線向量平行向量又稱共線向量abcabc兩向量的共線與平面幾何里兩線段的共線是否一樣�����?兩向量的共線與平面幾何里兩線段的共線是否一樣���?abc稱 、 �、 為線共共向向量量. .a/ b/ c如圖�����,某人從點如圖�����,某人從點A A到點到點B B��,再從點�����,再從點B B按原按原方向到點方向到點C C����,則兩次位移的和可用哪個���,則兩次位移的和可用哪個向量表示����?由此可得什么結(jié)論��?向量表示?由此可得什么結(jié)論�����?A B CACBCAB五五.探究探究如圖����,某人從點如圖,某人從點A A到點到點B
4�、 B,再從點����,再從點B B按反按反方向到點方向到點C C,則兩次位移的和可用哪個�����,則兩次位移的和可用哪個向量表示�?由此可得什么結(jié)論����?向量表示?由此可得什么結(jié)論��?ACBCABA B C探究探究從點從點A A到點到點B B,再從點�,再從點B B改變方向到點改變方向到點C C,則��,則兩次位移的和可用哪個向量表示如圖����,某兩次位移的和可用哪個向量表示如圖,某人由此可得什么結(jié)論�?人由此可得什么結(jié)論?A BCACBCAB探究探究已知非零向量已知非零向量 �,如何用三角形法則,如何用三角形法則求其和向量��?求其和向量�����?三角形法則:首尾相接連端點三角形法則:首尾相接連端點探究探究ab與abABaCbab上述求兩個向
5���、量和的方法���,稱為向量加法的上述求兩個向量和的方法,稱為向量加法的平行四邊形法則平行四邊形法則. .對于下列兩個向量對于下列兩個向量 與與 �,如何用平行四邊形法則求其和向量�����?如何用平行四邊形法則求其和向量��?BAOC平行四邊形法則:起點相同連對角平行四邊形法則:起點相同連對角. .探究探究abaababb零向量零向量 與任一向量與任一向量 和等于和等于規(guī)定規(guī)定:探究探究aa00aa若向量若向量 與與 為相反向量���,則為相反向量,則ab0ab 與與 為相反向量為相反向量ab0ab (1)(1)和和解解. .BCOABCOA (2).(2).BCBC (3)(3)雖雖然然��,且且= =�����,但但它它們們方方向
6�、向相相反反, ,故故這這兩兩個個向向量量并并不不相相等等. .OABCOABCOABCOABCOFEFEOABC 例例1 1:已已知知為為正正六六邊邊形形的的中中心心,在在圖圖中中所所標標出出的的向向量量中中:(1 1)試試找找出出與與共共線線的的向向量量�;(2 2)確確定定與與相相等等的的向向量量;(3 3) 與與相相等等嗎嗎�����?若若不不相相等等�,則則它它們們之之間間有有什什么么關(guān)關(guān)系系�?A AB BC CD DE EF FABCDEFOA AB BC CD DE EF FO O變式變式1:1:以圖中以圖中A,B,C,D,E,F,OA,B,C,D,E,F,O七點中的任一七點中的任一點為始點���,與
7、始點不同的另一點為終點的點為始點��,與始點不同的另一點為終點的所有向量中����,與向量所有向量中,與向量 相等的向量有幾相等的向量有幾個����?個?變式變式2 2: 的共線向量有幾個�����?的共線向量有幾個����?3 3個個9 9個個OAOA例例2 2:在圖中的:在圖中的 方格紙中有一個向量方格紙中有一個向量 ,分別以圖中的格點為起點和終點作向量�,其中與分別以圖中的格點為起點和終點作向量,其中與 相等的向量有多少個�?與相等的向量有多少個?與 長度相等的共線向量長度相等的共線向量有多少個�?(有多少個�����?( 除外)除外)3 4AB AB AB AB 7AB (1)共有 個向量與相等(2)15AB 共有個向量與共線A AB B
8����、AAB)(./,/,/. 1”則判斷正誤:“若cacbba()ac0b 3 3��、 判斷下列命題是否正確:判斷下列命題是否正確:(1 1)若兩個單位向量共線����,則這兩個向)若兩個單位向量共線,則這兩個向 量相等����;量相等; ( )(2 2)不相等的兩個向量一定不共線�����;)不相等的兩個向量一定不共線�����; ( )(3 3)在四邊形)在四邊形ABCDABCD中���,若向量中�,若向量 與與 共線�����,則該四邊形是梯形�����;(共線���,則該四邊形是梯形�;( )(4 4)對于不同三點)對于不同三點O O�����、A A����、B B,向量�,向量 與與 一定不共線一定不共線. . ( )ABCDOAOBABCDEFO1(2)(3)OABCDEFO
9、A OCBCFEOAFE 例1:已知 為正六邊形的中心�,作出下列向量();1OBOCOA)解:(;2ADFEBC)(. 03 FEOA)(4.5.在下列命題中����,正確的是 ( );,.babaA則若;,.babaB則若;/,.babaC則若 .,.共線一定不與則若babaDC6.給出下列命題平行向量的方向一定相同.共線向量一定在同一條直線上.不平行的向量一定不相等.與任意向量平行的向量是零向量.平行于同一個非零向量的向量是平行向量.其中�,所有正確命題的序號是 7.化簡下列各式:OBOPPB) 1 (OBOPPB) 1 (OBPBOP)(OBOBOB2解:.)(2(OMBOMBAB)()()(2MBOMBOABOMBOMBAB)解:(.ABOBAOBOOCCAOBAO)3(BOOCCAOBAO)3(解:BOCAOCOBAO)()(BOOAABOABOAB)(0OAAO
 內(nèi)蒙古滿洲里市第七中學高中數(shù)學 第二章平面向量《向量加法練習》課件 新人教A版必修4
內(nèi)蒙古滿洲里市第七中學高中數(shù)學 第二章平面向量《向量加法練習》課件 新人教A版必修4