陜西省山陽縣色河鋪鎮(zhèn)2018年中考數(shù)學(xué)總復(fù)習(xí) 第12講 二次函數(shù)的圖象與性質(zhì)

《陜西省山陽縣色河鋪鎮(zhèn)2018年中考數(shù)學(xué)總復(fù)習(xí) 第12講 二次函數(shù)的圖象與性質(zhì)》由會員分享，可在線閱讀，更多相關(guān)《陜西省山陽縣色河鋪鎮(zhèn)2018年中考數(shù)學(xué)總復(fù)習(xí) 第12講 二次函數(shù)的圖象與性質(zhì)（3頁珍藏版）》請在裝配圖網(wǎng)上搜索。

1、第12講 二次函數(shù)的圖象與性質(zhì) 一、 知識清單梳理 知識點一：二次函數(shù)的概念及解析式 關(guān)鍵點撥與對應(yīng)舉例 1.二次函數(shù)的定義 形如y＝ax2＋bx＋c (a，b，c是常數(shù)，a≠0)的函數(shù)，叫做二次函數(shù). 例：如果函數(shù)y=(a－1)x2是二次函數(shù)，那么a的取值范圍是a≠0. 2.解析式 （1）三種解析式：①一般式：y=ax2+bx+c;②頂點式：y=a(x-h)2+k(a≠0)，其中二次函數(shù)的頂點坐標是（h,k）; ③交點式：y=a(x-x1)(x-x2),其中x1,x2為拋物線與x軸交點的橫坐標. （2）待定系數(shù)法：巧設(shè)二次函數(shù)的解析式；根據(jù)已知條件，得到關(guān)于待定系數(shù)的方

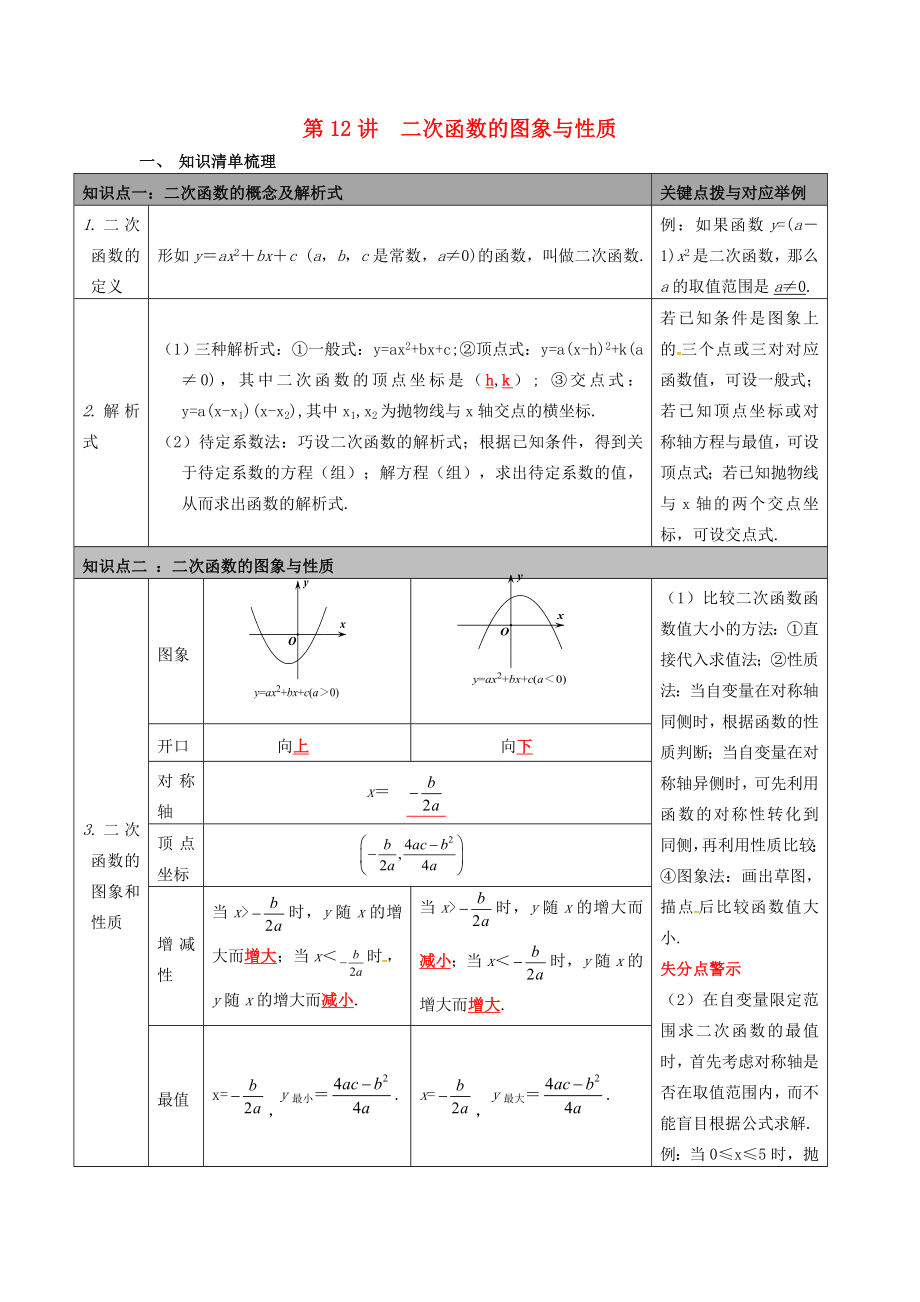
2、程（組）；解方程（組），求出待定系數(shù)的值，從而求出函數(shù)的解析式. 若已知條件是圖象上的三個點或三對對應(yīng)函數(shù)值，可設(shè)一般式；若已知頂點坐標或?qū)ΨQ軸方程與最值，可設(shè)頂點式；若已知拋物線與x軸的兩個交點坐標，可設(shè)交點式. 知識點二 ：二次函數(shù)的圖象與性質(zhì) 3.二次函數(shù)的圖象和性質(zhì) 圖象 （1）比較二次函數(shù)函數(shù)值大小的方法：①直接代入求值法；②性質(zhì)法：當(dāng)自變量在對稱軸同側(cè)時，根據(jù)函數(shù)的性質(zhì)判斷；當(dāng)自變量在對稱軸異側(cè)時，可先利用函數(shù)的對稱性轉(zhuǎn)化到同側(cè)，再利用性質(zhì)比較；④圖象法：畫出草圖，描點后比較函數(shù)值大小. 失分點警示 （2）在自變量限定范圍求二次函數(shù)的最值時，首先考慮對稱軸是否

3、在取值范圍內(nèi)，而不能盲目根據(jù)公式求解. 例：當(dāng)0≤x≤5時，拋物線y=x2+2x+7的最小值為7 . 開口 向上 向下 對稱軸 x＝ 頂點坐標 增減性 當(dāng)x>時，y隨x的增大而增大；當(dāng)x＜時，y隨x的增大而減小. 當(dāng)x>時，y隨x的增大而減小；當(dāng)x＜時，y隨x的增大而增大. 最值 x=，y最?。? x=，y最大＝. 3.系數(shù)a、b、c a 決定拋物線的開口方向及開口大小 當(dāng)a＞0時，拋物線開口向上； 當(dāng)a＜0時，拋物線開口向下. 某些特殊形式代數(shù)式的符號： ① a±b+c即為x=±1時，y 的值；②4a±2b+c即為x=±2時，y的值

4、. ③ 2a+b的符號，需判斷對稱 軸-b/2a與1的大小.若對稱軸在直線x=1的左邊，則-b/2a＞1，再根據(jù)a的符號即可得出結(jié)果.④2a-b的符號，需判斷對稱軸與-1的大小. a、 b 決定對稱軸（x=-b/2a）的位置 當(dāng)a，b同號，-b/2a＜0，對稱軸在y軸左邊； 當(dāng)b＝0時， -b/2a=0，對稱軸為y軸； 當(dāng)a，b異號，-b/2a＞0，對稱軸在y軸右邊． c 決定拋物線與y軸的交點的位置 當(dāng)c＞0時，拋物線與y軸的交點在正半軸上； 當(dāng)c＝0時，拋物線經(jīng)過原點； 當(dāng)c＜0時，拋物線與y軸的交點在負半軸上. b2－4ac 決定拋物線與x軸的交點個數(shù)

5、 b2－4ac＞0時，拋物線與x軸有2個交點; b2－4ac＝0時，拋物線與x軸有1個交點; b2－4ac＜0時，拋物線與x軸沒有交點 知識點三 ：二次函數(shù)的平移 4.平移與解析式的關(guān)系 注意：二次函數(shù)的平移實質(zhì)是頂點坐標的平移，因此只要找出原函數(shù)頂點的平移方式即可確定平移后的函數(shù)解析式 失分點警示： 拋物線平移規(guī)律是“上加下減，左加右減”,左右平移易弄反. 例：將拋物線y=x2沿x軸向右平移2個單位后所得拋物線的解析式是y=（x－2）2． 知識點四 ：二次函數(shù)與一元二次方程以及不等式 5.二次函數(shù)與一元二次方程 二次函數(shù)y=ax2＋bx＋c(a≠0)的圖象與x軸交點

6、的橫坐標是一元二次方程ax2+bx+c=0的根. 當(dāng)Δ＝b2－4ac＞0，兩個不相等的實數(shù)根； 當(dāng)Δ＝b2－4ac＝0，兩個相等的實數(shù)根； 當(dāng)Δ＝b2－4ac＜0，無實根 例：已經(jīng)二次函數(shù)y=x2-3x+m(m為常數(shù))的圖象與x軸的一個交點為（1,0），則關(guān)于x的一元二次方程x2-3x+m=0的兩個實數(shù)根為2,1. 6. 二次函數(shù)與不等式 拋物線y= ax2＋bx＋c＝0在x軸上方的部分點的縱坐標都為正，所對應(yīng)的x的所有值就是不等式ax2＋bx＋c＞0的解集；在x軸下方的部分點的縱坐標均為負，所對應(yīng)的x的值就是不等式ax2＋bx＋c＜0的解集. 知識點一：二次函數(shù)的應(yīng)用

7、 關(guān)鍵點撥 實物拋物線 一般步驟 若題目中未給出坐標系，則需要建立坐標系求解，建立的原則：①所建立的坐標系要使求出的二次函數(shù)表達式比較簡單；②使已知點所在的位置適當(dāng)（如在x軸，y軸、原點、拋物線上等），方便求二次函數(shù)丶表達式和之后的計算求解. ① 據(jù)題意，結(jié)合函數(shù)圖象求出函數(shù)解析式； ②確定自變量的取值范圍； ③根據(jù)圖象，結(jié)合所求解析式解決問題. 實際問題中 求最值 ① 分析問題中的數(shù)量關(guān)系，列出函數(shù)關(guān)系式； ② 研究自變量的取值范圍； ③ 確定所得的函數(shù)； ④ 檢驗x的值是否在自變量的取值范圍內(nèi)，并求相關(guān)的值； ⑤解決提出的實際問題

8、. 解決最值應(yīng)用題要注意兩點： ①設(shè)未知數(shù)，在“當(dāng)某某為何值時，什么最大（最?。钡脑O(shè)問中，“某某”要設(shè)為自變量，“什么”要設(shè)為函數(shù)； ②求解最值時，一定要考慮頂點（橫、縱坐標）的取值是否在自變量的取值范圍內(nèi). 結(jié)合幾何圖形 ① 根據(jù)幾何圖形的性質(zhì)，探求圖形中的關(guān)系式； ② 根據(jù)幾何圖形的關(guān)系式確定二次函數(shù)解析式； ③ 利用配方法等確定二次函數(shù)的最值，解決問題 由于面積等于兩條邊的乘積，所以幾何問題的面積的最值問題通常會通過二次函數(shù)來解決.同樣需注意自變量的取值范圍. 二、 典例講解 內(nèi)參P44------3、4、6、7、10、11、12、14、16 P46-----19、20、4、5、7、8、9、13 三、課后反思：