《江蘇省蘇州市第五中學(xué)高中數(shù)學(xué) 第一章單元復(fù)習(xí)學(xué)案（無答案）蘇教版選修2-2》由會(huì)員分享，可在線閱讀，更多相關(guān)《江蘇省蘇州市第五中學(xué)高中數(shù)學(xué) 第一章單元復(fù)習(xí)學(xué)案（無答案）蘇教版選修2-2（3頁珍藏版）》請?jiān)谘b配圖網(wǎng)上搜索。
1、第1章 導(dǎo)數(shù)及其運(yùn)用單元復(fù)習(xí)
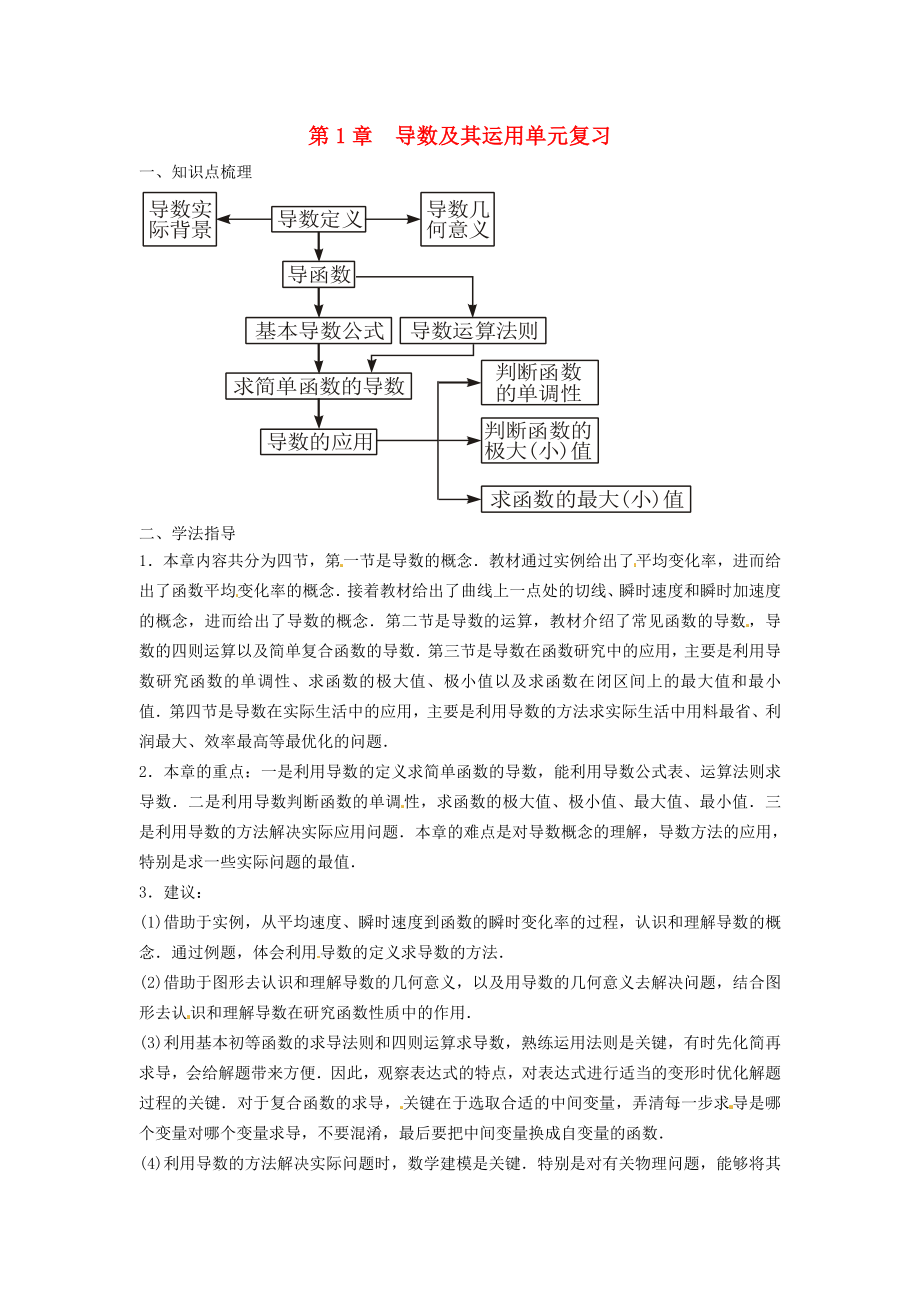
一、知識(shí)點(diǎn)梳理
二、學(xué)法指導(dǎo)
1．本章內(nèi)容共分為四節(jié)，第一節(jié)是導(dǎo)數(shù)的概念．教材通過實(shí)例給出了平均變化率，進(jìn)而給出了函數(shù)平均變化率的概念．接著教材給出了曲線上一點(diǎn)處的切線、瞬時(shí)速度和瞬時(shí)加速度的概念，進(jìn)而給出了導(dǎo)數(shù)的概念．第二節(jié)是導(dǎo)數(shù)的運(yùn)算，教材介紹了常見函數(shù)的導(dǎo)數(shù)，導(dǎo)數(shù)的四則運(yùn)算以及簡單復(fù)合函數(shù)的導(dǎo)數(shù)．第三節(jié)是導(dǎo)數(shù)在函數(shù)研究中的應(yīng)用，主要是利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性、求函數(shù)的極大值、極小值以及求函數(shù)在閉區(qū)間上的最大值和最小值．第四節(jié)是導(dǎo)數(shù)在實(shí)際生活中的應(yīng)用，主要是利用導(dǎo)數(shù)的方法求實(shí)際生活中用料最省、利潤最大、效率最高等最優(yōu)化的問題．
2．本章的重點(diǎn)：一
2、是利用導(dǎo)數(shù)的定義求簡單函數(shù)的導(dǎo)數(shù)，能利用導(dǎo)數(shù)公式表、運(yùn)算法則求導(dǎo)數(shù)．二是利用導(dǎo)數(shù)判斷函數(shù)的單調(diào)性，求函數(shù)的極大值、極小值、最大值、最小值．三是利用導(dǎo)數(shù)的方法解決實(shí)際應(yīng)用問題．本章的難點(diǎn)是對導(dǎo)數(shù)概念的理解，導(dǎo)數(shù)方法的應(yīng)用，特別是求一些實(shí)際問題的最值．
3．建議：
(1)借助于實(shí)例，從平均速度、瞬時(shí)速度到函數(shù)的瞬時(shí)變化率的過程，認(rèn)識(shí)和理解導(dǎo)數(shù)的概念．通過例題，體會(huì)利用導(dǎo)數(shù)的定義求導(dǎo)數(shù)的方法．
(2)借助于圖形去認(rèn)識(shí)和理解導(dǎo)數(shù)的幾何意義，以及用導(dǎo)數(shù)的幾何意義去解決問題，結(jié)合圖形去認(rèn)識(shí)和理解導(dǎo)數(shù)在研究函數(shù)性質(zhì)中的作用．
(3)利用基本初等函數(shù)的求導(dǎo)法則和四則運(yùn)算求導(dǎo)數(shù)，熟練運(yùn)用法則是關(guān)鍵，有時(shí)
3、先化簡再求導(dǎo)，會(huì)給解題帶來方便．因此，觀察表達(dá)式的特點(diǎn)，對表達(dá)式進(jìn)行適當(dāng)?shù)淖冃螘r(shí)優(yōu)化解題過程的關(guān)鍵．對于復(fù)合函數(shù)的求導(dǎo)，關(guān)鍵在于選取合適的中間變量，弄清每一步求導(dǎo)是哪個(gè)變量對哪個(gè)變量求導(dǎo)，不要混淆，最后要把中間變量換成自變量的函數(shù)．
(4)利用導(dǎo)數(shù)的方法解決實(shí)際問題時(shí)，數(shù)學(xué)建模是關(guān)鍵．特別是對有關(guān)物理問題，能夠?qū)⑵湮锢硪饬x與求導(dǎo)數(shù)聯(lián)系起來．
三、單元自測
(一) 填空題(每小題5分，共70分)
1．半徑為R的圓受熱均勻膨脹，若半徑增加了r，則圓面積的平均膨脹率是__________．
2．已知函數(shù)，則=__________________．
3．已知函數(shù)y＝log (3x＋1)
4、，則它的導(dǎo)數(shù)為_______________．
4．如圖，函數(shù)的圖象在點(diǎn)P處的切線方程是，
則= ．
5．若，則當(dāng)h無限趨近于0時(shí)，→____．
6．已知函數(shù)在x=0處取得最大值，在x=2處取得最小值，則m的取值范圍是 ．
7．要做一個(gè)母線長為20厘米的圓錐形的漏斗，當(dāng)高為 厘米時(shí)，該漏斗的體積最大?
8．設(shè)函數(shù)在上是單調(diào)函數(shù)，則實(shí)數(shù)的取值范圍為________．
9．若函數(shù)f(x)=在其定義域內(nèi)沒有極值，則a的取值范圍為_________．
10．若上是減函數(shù)，則的取值范圍是__________．
5、11．設(shè)曲線在點(diǎn)處的切線與直線垂直，則___________．
12．設(shè)函數(shù)，若 是奇函數(shù)，則__________．
13．函數(shù)f (x)=x3－3x，的最小值為－2，則實(shí)數(shù)的值為__________．
14．已知是定義在上的奇函數(shù)，當(dāng)時(shí)，． 若函數(shù)在其定義域上有且僅有四個(gè)不同的零點(diǎn)，則實(shí)數(shù)的取值范圍是 ．
(二) 解答題(15、16每小題13分，17~20每小題16分，共90分)
15．如果曲線的某一條切線與直線平行，求切點(diǎn)坐標(biāo)和切線方程．
16．已知是實(shí)數(shù)，函數(shù)，求函數(shù)的單調(diào)區(qū)間．
17．如圖，在矩形地塊ABCD中有兩條道路AF，EC，其中AF是以A為頂點(diǎn)的拋物線段，EC是線段．AB=2km，BC=6km，AE=BF=4km．在兩條道路之間計(jì)劃修建一個(gè)公園，公園的形狀為直角梯形QPRE(線段EQ和RP為兩個(gè)底邊，如圖所示)．求該公園的最大面積．
18．設(shè)函數(shù)
(1)求函數(shù)的單調(diào)區(qū)間；
(2)已知對任意成立，求實(shí)數(shù)的取值范圍．
19．已知，，．
(1)當(dāng)a=1時(shí)，求的單調(diào)區(qū)間；
(2)是否存在實(shí)數(shù)a，使的極大值為3?若存在，求出a的值，若不存在，請說明理由．
20．已知函數(shù)，，且）．
(1)討論函數(shù)的單調(diào)性；
(2)若，關(guān)于的方程有唯一解，求a的值．
江蘇省蘇州市第五中學(xué)高中數(shù)學(xué) 第一章單元復(fù)習(xí)學(xué)案（無答案）蘇教版選修2-2
