《2019屆高考數(shù)學二輪復習 第二部分 突破熱點 分層教學 專項二 專題七 2 第2講 不等式選講學案》由會員分享���,可在線閱讀��,更多相關《2019屆高考數(shù)學二輪復習 第二部分 突破熱點 分層教學 專項二 專題七 2 第2講 不等式選講學案(12頁珍藏版)》請在裝配圖網(wǎng)上搜索���。
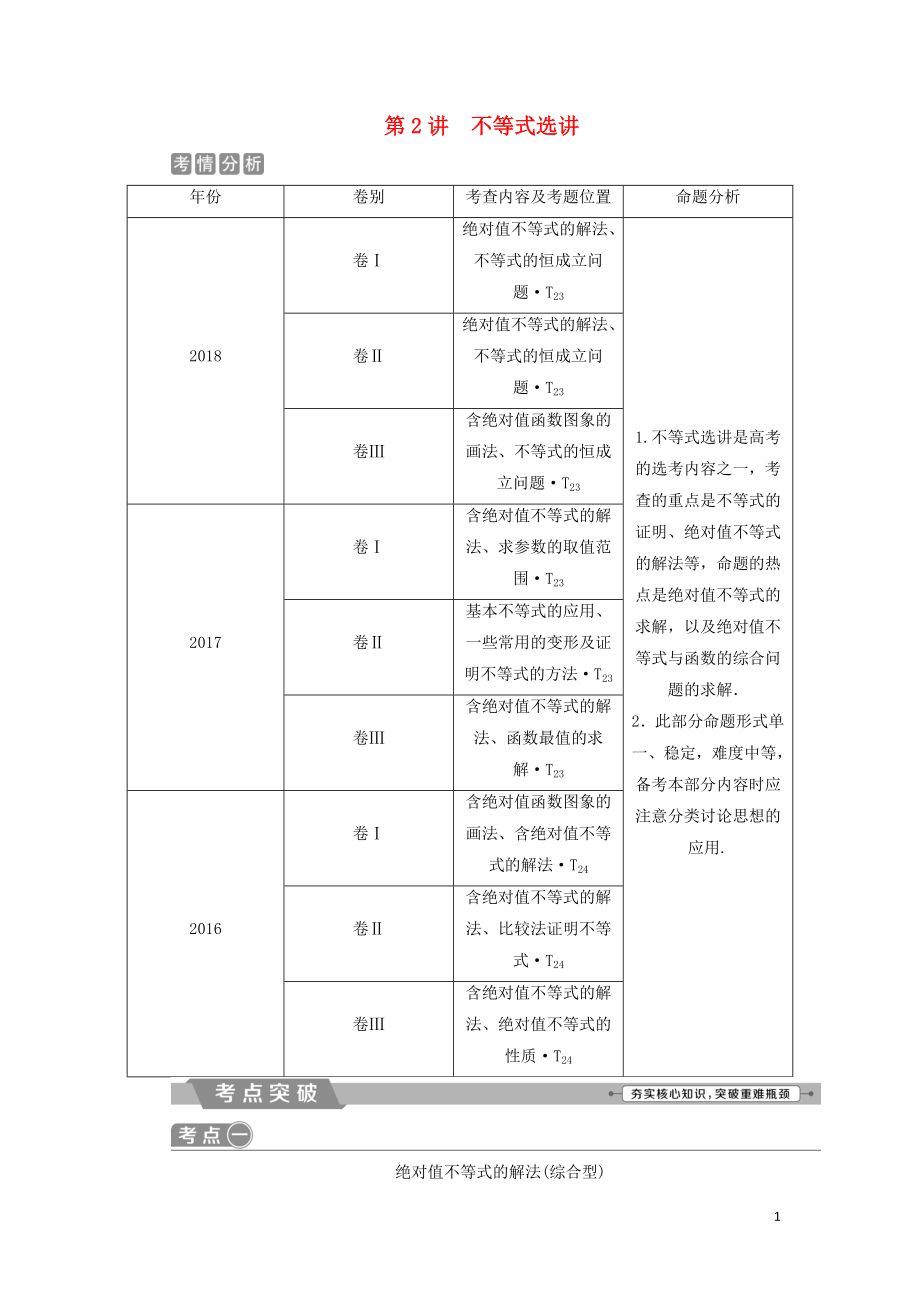
1��、第2講不等式選講年份卷別考查內容及考題位置命題分析2018卷絕對值不等式的解法�、不等式的恒成立問題T231.不等式選講是高考的選考內容之一�,考查的重點是不等式的證明�����、絕對值不等式的解法等����,命題的熱點是絕對值不等式的求解��,以及絕對值不等式與函數(shù)的綜合問題的求解2此部分命題形式單一����、穩(wěn)定,難度中等�����,備考本部分內容時應注意分類討論思想的應用.卷絕對值不等式的解法��、不等式的恒成立問題T23卷含絕對值函數(shù)圖象的畫法、不等式的恒成立問題T232017卷含絕對值不等式的解法��、求參數(shù)的取值范圍T23卷基本不等式的應用�、一些常用的變形及證明不等式的方法T23卷含絕對值不等式的解法、函數(shù)最值的求解T232016卷
2��、含絕對值函數(shù)圖象的畫法����、含絕對值不等式的解法T24卷含絕對值不等式的解法���、比較法證明不等式T24卷含絕對值不等式的解法�、絕對值不等式的性質T24絕對值不等式的解法(綜合型)含有絕對值的不等式的解法(1)|f(x)|a(a0)f(x)a或f(x)a��;(2)|f(x)|0)af(x)a����;(3)對形如|xa|xb|c,|xa|xb|c的不等式�,可利用絕對值不等式的幾何意義求解 典型例題 (2018太原模擬)已知函數(shù)f(x)|xm|2x1|.(1)當m1時����,求不等式f(x)2的解集�;(2)若f(x)|2x1|的解集包含,求m的取值范圍【解】(1)當m1時����,f(x)|x1|2x1|�����,當x1時���,f(x)3
3�����、x22�,所以1x����;當x1時,f(x)x2�,所以x0),|xa|xb|c(或c)(c0)型不等式的解法可通過零點分區(qū)間法或利用絕對值的幾何意義進行求解(1)零點分區(qū)間法的一般步驟令每個絕對值符號的代數(shù)式為零�����,并求出相應的根將這些根按從小到大排列��,把實數(shù)集分為若干個區(qū)間由所分區(qū)間去掉絕對值符號得若干個不等式���,解這些不等式��,求出解集取各個不等式解集的并集就是原不等式的解集(2)利用絕對值的幾何意義由于|xa|xb|與|xa|xb|分別表示數(shù)軸上與x對應的點到a���,b對應的點的距離之和與距離之差,因此對形如|xa|xb|c(或c)(c0)或|xa|xb|c(或c)(c0)的不等式���,利用絕對值的幾何意義求
4�、解更直觀 對點訓練(2018合肥第一次質量檢測)已知函數(shù)f(x)|2x1|.(1)解關于x的不等式f(x)f(x1)1����;(2)若關于x的不等式f(x)mf(x1)的解集不是空集,求m的取值范圍解:(1)f(x)f(x1)1|2x1|2x1|1���,則或或解得x或x�����,即x����,所以原不等式的解集為.(2)由條件知,不等式|2x1|2x1|(|2x1|2x1|)min即可由于|2x1|2x1|12x|2x1|12x2x1|2��,當且僅當(12x)(2x1)0�,即x時等號成立,故m2.所以m的取值范圍是(2���,)不等式的證明(綜合型) 含有絕對值的不等式的性質|a|b|ab|a|b|. 算術幾何平均不等式定理1
5��、:設a���,bR,則a2b22ab�����,當且僅當ab時,等號成立定理2:如果a����,b為正數(shù)�,則,當且僅當ab時�����,等號成立定理3:如果a��,b�����,c為正數(shù)�����,則����,當且僅當abc時,等號成立定理4:(一般形式的算術幾何平均不等式)如果a1�����,a2,an為n個正數(shù)��,則���,當且僅當a1a2an時���,等號成立 典型例題 (2018長春質量檢測(一)設不等式|x1|x1|1.【解】(1)由已知,令f(x)|x1|x1|由|f(x)|2得1x1�����,即Ax|1x1��,只需證|1abc|abc|���,只需證1a2b2c2a2b2c2���,只需證1a2b2c2(1a2b2),只需證(1a2b2)(1c2)0�����,由a,b���,cA��,得a2b21�,c20恒
6����、成立綜上����,1.證明不等式的方法和技巧(1)如果已知條件與待證明的結論直接聯(lián)系不明顯,可考慮用分析法���;如果待證的命題以“至少”“至多”等方式給出或是否定性命題�����、唯一性命題���,則考慮用反證法(2)在必要的情況下,可能還需要使用換元法��、構造法等技巧簡化對問題的表述和證明尤其是對含絕對值不等式的解法或證明,其簡化的基本思路是化去絕對值符號�,轉化為常見的不等式(組)求解多以絕對值的幾何意義或“找零點、分區(qū)間�����、逐個解����、并起來”為簡化策略,而絕對值三角不等式��,往往作為不等式放縮的依據(jù)對點訓練(2018陜西教學質量檢測(一)已知函數(shù)f(x)|2x1|x1|.(1)解不等式f(x)3�;(2)記函數(shù)g(x)f(x)
7、|x1|的值域為M�,若tM,證明t213t.解:(1)依題意�����,得f(x)所以f(x)3或或解得1x1�,即不等式f(x)3的解集為x|1x1(2)證明:g(x)f(x)|x1|2x1|2x2|2x12x2|3,當且僅當(2x1)(2x2)0時取等號���,所以M3��,)t213t���,因為tM��,所以t30�,t210�,所以0,所以t213t.含絕對值不等式的恒成立問題(綜合型)典型例題 (2018鄭州第一次質量預測)設函數(shù)f(x)|x3|�,g(x)|2x1|.(1)解不等式f(x)ax4對任意的實數(shù)x恒成立,求a的取值范圍【解】(1)由已知���,可得|x3|2x1|,即|x3|20�����,解得x4.故所求不等式的解集為
8�����、(4�,)(2)由已知�,設h(x)2f(x)g(x)2|x3|2x1|當x3時����,只需4x5ax4恒成立�����,即ax4x9恒成立��,因為x34恒成立����,所以a���,所以a1;當3xax4恒成立���,即ax3ax4恒成立��,即ax0���,所以a4,且x時���,44�,所以a4.綜上����,a的取值范圍是(1,4絕對值不等式的成立問題的求解模型(1)分離參數(shù):根據(jù)不等式將參數(shù)分離化為af(x)或af(x)形式(2)轉化最值:f(x)a恒成立f(x)mina�;f(x)a恒成立f(x)maxa有解f(x)maxa��;f(x)a有解f(x)mina無解f(x)maxa����;f(x)1的解集為x|x(2)當x(0,1)時|x1|ax1|x成立等價于
9�����、當x(0,1)時|ax1|0����,|ax1|1的解集為0x,所以1���,故04|a1|�,求實數(shù)a的取值范圍�����;(2)若存在實數(shù)x����,y,使f(x)g(y)0�����,求實數(shù)a的取值范圍解:(1)因為f(2a21)4|a1|���,所以|2a22a|a21|4|a1|,所以|a1|(2|a|a1|4)0�����,所以|2a|a1|4且a1.若a1��,則2aa14����,所以a;若1a4�����,所以a4���,所以a1.綜上所述�,a的取值范圍為(1���,)(2)因為g(x)(x1)25251,顯然可取等號��,所以g(x)min1.于是�,若存在實數(shù)x,y��,使f(x)g(y)0,只需f(x)min1.又f(x)|x12a|xa2|(x12a)(xa2)|(a1
10����、)2���,所以(a1)21,所以1a11��,所以0a2�����,即a0��,21(2018高考全國卷)設函數(shù)f(x)5|xa|x2|.(1)當a1時��,求不等式f(x)0的解集��;(2)若f(x)1,求a的取值范圍解:(1)當a1時�����,f(x)可得f(x)0的解集為x|2x3(2)f(x)1等價于|xa|x2|4.而|xa|x2|a2|��,且當x2時等號成立故f(x)1等價于|a2|4.由|a2|4可得a6或a2.所以a的取值范圍是(�����,62,)2(2018開封模擬)已知函數(shù)f(x)|xm|����,m0.(1)當m1時��,求解不等式f(x)f(x)2x�;(2)若不等式f(x)f(2x)1的解集非空,求m的取值范圍解:(1)設F(
11����、x)|x1|x1|由F(x)G(x)解得x|x2或x0(2)f(x)f(2x)|xm|2xm|��,m0.設g(x)f(x)f(2x)�����,當xm時��,g(x)mxm2x2m3x�����,則g(x)m�;當mx時���,g(x)xmm2xx�,則g(x)m�����;當x時���,g(x)xm2xm3x2m,則g(x).則g(x)的值域為�,不等式f(x)f(2x),解得m2���,由于m0的解集;(2)若函數(shù)f(x)的圖象與x軸沒有交點���,求實數(shù)a的取值范圍解:(1)當a3時�����,不等式可化為|3x1|x0�����,即|3x1|x��,所以3x1x�����,即x����,所以不等式f(x)0的解集為.(2)當a0時���,f(x)要使函數(shù)f(x)的圖象與x軸無交點,只需即1a2��;當
12�、a0時,f(x)2x1��,函數(shù)f(x)的圖象與x軸有交點����,不合題意;當a1且x時����,f(x)g(x)����,求實數(shù)a的取值范圍解:(1)當a1時,f(x).當x時�����,f(x)2無解綜上所述���,f(x)2的解集為.(2)當x時,f(x)(a2x)(2x1)a1����,所以f(x)g(x)可化為a1g(x)又g(x)4x2ax3在上的最大值必為g、g之一���,則�,即�����,即a2.又a1��,所以1a2��,所以a的取值范圍為(1�����,26(2018南昌模擬)已知函數(shù)f(x)|2x3a2|.(1)當a0時��,求不等式f(x)|x2|3的解集�;(2)若對于任意函數(shù)x����,不等式|2x1|f(x)2a恒成立�����,求實數(shù)a的取值范圍解:(1)當a0時���,不
13���、等式可化為|2x|x2|3,得或或����,解得x或x1,所以當a0時��,不等式f(x)|x2|3的解集為1�����,)(2)對于任意實數(shù)x,不等式|2x1|f(x)2a恒成立���,即|2x1|2x3a2|2a恒成立因為|2x1|2x3a2|2x12x3a2|3a21|���,所以要使原不等式恒成立,只需|3a21|2a.當a0時����,無解���;當0a時����,13a22a,解得時�����,3a212a�,解得a1.所以實數(shù)a的取值范圍是.7(2018福州模擬)已知函數(shù)f(x)x2|x|1.(1)求不等式f(x)2x的解集���;(2)若關于x的不等式f(x)在0�����,)上恒成立��,求實數(shù)a的取值范圍解:(1)不等式f(x)2x等價于x2|x|2x10����,當
14�����、x0時�����,式化為x23x10���,解得x或0x�;當x0時�����,式化為x2x10,解得xg(x)的解集����;(2)若對任意x1,x2R�,不等式f(x1)g(x2)恒成立,求實數(shù)a的取值范圍解:(1)當a4時��,不等式f(x)g(x)為x22|x4|x1|����,g(x)|x4|x1|當x4時,x223恒成立���,所以x4.當1x2x5�,即x22x30����,得x1或x3,所以1x3��,則x1或x1�����,所以xg(x)的解集為x|x1(2)當a1時���,g(x)所以g(x)的最大值為a1.要使f(x1)g(x2),只需2a1���,則a3��,所以1a3.當a1時��,g(x)所以g(x)的最大值為1a.要使f(x1)g(x2)���,只需21a,則a1���,所以1a1.綜上��,實數(shù)a的取值范圍是1,3.12
 2019屆高考數(shù)學二輪復習 第二部分 突破熱點 分層教學 專項二 專題七 2 第2講 不等式選講學案
2019屆高考數(shù)學二輪復習 第二部分 突破熱點 分層教學 專項二 專題七 2 第2講 不等式選講學案