高中數(shù)學(xué)人教A版選修11 第三章導(dǎo)數(shù)及其應(yīng)用 學(xué)業(yè)分層測評16 Word版含答案

《高中數(shù)學(xué)人教A版選修11 第三章導(dǎo)數(shù)及其應(yīng)用 學(xué)業(yè)分層測評16 Word版含答案》由會員分享，可在線閱讀，更多相關(guān)《高中數(shù)學(xué)人教A版選修11 第三章導(dǎo)數(shù)及其應(yīng)用 學(xué)業(yè)分層測評16 Word版含答案（7頁珍藏版）》請在裝配圖網(wǎng)上搜索。

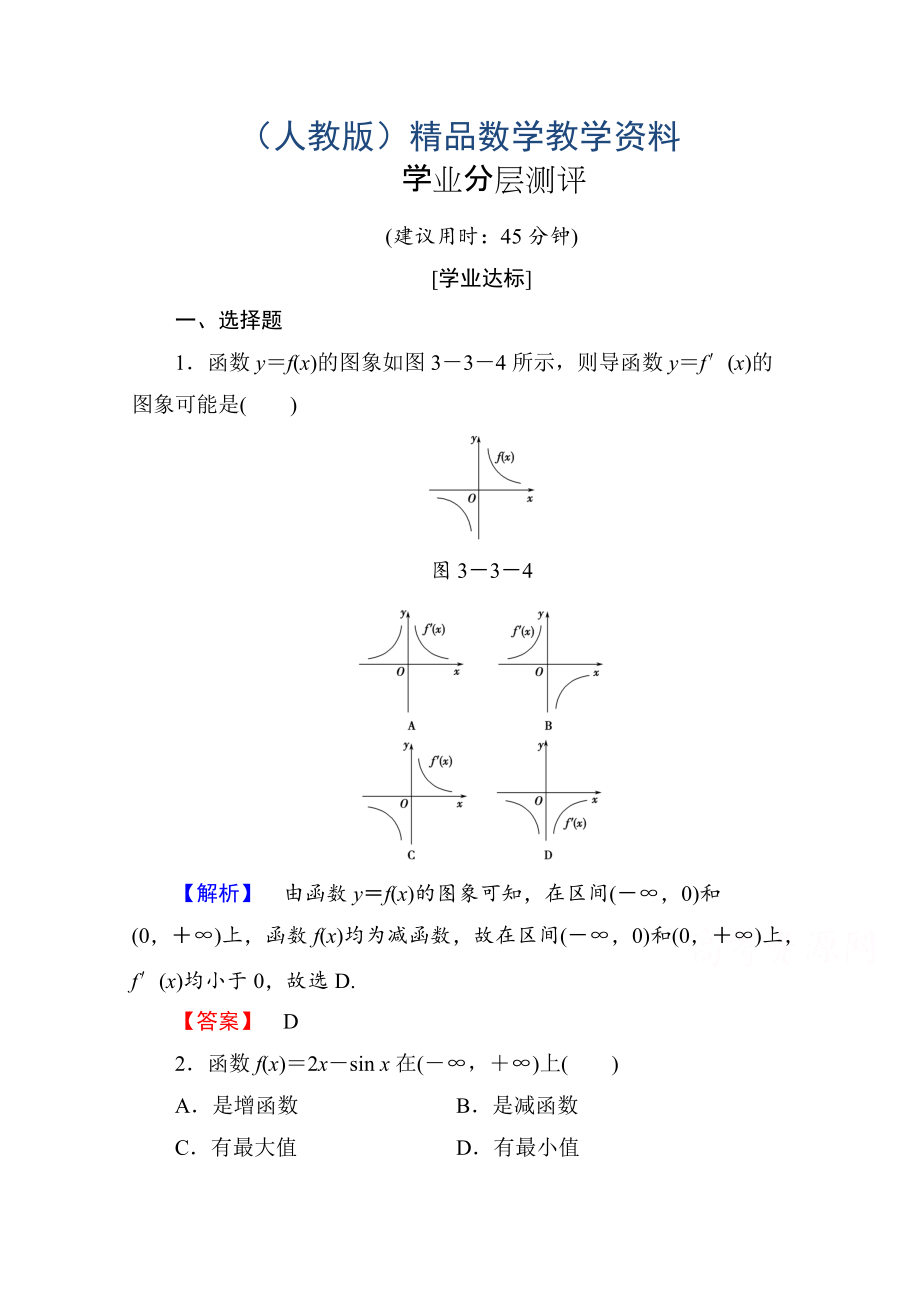
1、（人教版）精品數(shù)學(xué)教學(xué)資料學(xué)業(yè)分層測評(建議用時：45分鐘)學(xué)業(yè)達標一、選擇題1函數(shù)yf(x)的圖象如圖334所示，則導(dǎo)函數(shù)yf(x)的圖象可能是()圖334【解析】由函數(shù)yf(x)的圖象可知，在區(qū)間(，0)和(0，)上，函數(shù)f(x)均為減函數(shù)，故在區(qū)間(，0)和(0，)上，f(x)均小于0，故選D.【答案】D2函數(shù)f(x)2xsin x在(，)上()A是增函數(shù)B是減函數(shù)C有最大值D有最小值【解析】cos x1，f(x)2cos x>0恒成立，f(x)在(，)上為增函數(shù)【答案】A3函數(shù)y(3x2)ex的單調(diào)遞增區(qū)間是()A(，0)B(0，)C(，3)和(1，)D(3,1)【解析】y2xe

2、x(3x2)ex(x22x3)ex，令(x22x3)ex>0，由于ex>0，則x22x3>0，解得3<x<1，所以函數(shù)的單調(diào)遞增區(qū)間是(3,1)【答案】D4已知函數(shù)f(x)ln x，則有()Af(2)<f(e)<f(3)Bf(e)<f(2)<f(3)Cf(3)<f(e)<f(2)Df(e)<f(3)<f(2)【解析】因為在定義域(0，)上，f(x)>0，所以f(x)在(0，)上是增函數(shù)，所以有f(2)<f(e)<f(3)【答案】A5(2014·全國卷)若函數(shù)f(x)kxln x在區(qū)間(1，

3、)上單調(diào)遞增，則k的取值范圍是()A(，2B(，1C2，)D1，)【解析】由于f(x)k，f(x)kxln x在區(qū)間(1，)上單調(diào)遞增f(x)k0在(1，)上恒成立由于k，而0<<1，所以k1.即k的取值范圍為1，)【答案】D二、填空題6若函數(shù)f(x)x3bx2cxd的單調(diào)遞減區(qū)間為(1，2)，則b_，c_. 【導(dǎo)學(xué)號：26160084】【解析】f(x)3x22bxc，由題意知1<x<2是不等式f(x)<0的解，即1,2是方程3x22bxc0的兩個根，把1,2分別代入方程，解得b，c6.【答案】67函數(shù)yax31在(，)上是減函數(shù)，則a的取值范圍為_【解析】y3a

4、x20恒成立，解得a0.而a0時，y1，不是減函數(shù)，a<0.【答案】a<08在下列命題中，真命題是_(填序號)若f(x)在(a，b)內(nèi)是增函數(shù)，則對任意x(a，b)，都應(yīng)有f(x)>0；若在(a，b)內(nèi)f(x)存在，則f(x)必為單調(diào)函數(shù)；若在(a，b)內(nèi)對任意x都有f(x)>0，則f(x)在(a，b)內(nèi)是增函數(shù)；若可導(dǎo)函數(shù)在(a，b)內(nèi)有f(x)<0，則在(a，b)內(nèi)有f(x)<0.【解析】對于，可以存在x0，使f(x0)0不影響區(qū)間內(nèi)函數(shù)的單調(diào)性；對于，導(dǎo)數(shù)f(x)符號不確定，函數(shù)不一定是單調(diào)函數(shù)；對于，f(x)<0只能得到f(x)單調(diào)遞減【答案】

5、三、解答題9求下列函數(shù)的單調(diào)區(qū)間：(1)f(x)xsin x，x(0,2)；(2)f(x)2xln x.【解】(1)f(x)cos x，令f(x)>0，得cos x>0，即cos x>.又x(0,2)，0<x<或<x<2.同理，令f(x)<0，得<x<.該函數(shù)的單調(diào)遞增區(qū)間為，；單調(diào)遞減區(qū)間為.(2)函數(shù)的定義域為(0，)，其導(dǎo)函數(shù)為f(x)2.令2>0，解得x>；令2<0，解得0<x<，該函數(shù)的單調(diào)遞增區(qū)間為，單調(diào)遞減區(qū)間為.10若函數(shù)f(x)x3ax2(a1)x1在區(qū)間(1,4)內(nèi)為減函數(shù)，在區(qū)間(6

6、，)內(nèi)為增函數(shù)，試求實數(shù)a的取值范圍【解】函數(shù)求導(dǎo)得f(x)x2axa1(x1)x(a1)，令f(x)0得x1或xa1.因為函數(shù)在區(qū)間(1,4)內(nèi)為減函數(shù)，所以當x(1,4)時，f(x)0，又因為函數(shù)在區(qū)間(6，)內(nèi)為增函數(shù)，所以當x(6，)時，f(x)0，所以4a16，所以5a7，即實數(shù)a的取值范圍為5,7能力提升1已知函數(shù)yxf(x)的圖象如圖335所示，下面四個圖象中能大致表示yf(x)的圖象的是()圖335【解析】由題圖可知，當x<1時，xf(x)<0，所以f(x)>0，此時原函數(shù)為增函數(shù)，圖象應(yīng)是上升的；當1<x<0時，xf(x)>0，所以f(x)

7、<0，此時原函數(shù)為減函數(shù)，圖象應(yīng)是下降的；當0<x<1時，xf(x)<0，所以f(x)<0，此時原函數(shù)為減函數(shù)，圖象應(yīng)是下降的；當x>1時，xf(x)>0，所以f(x)>0，此時原函數(shù)為增函數(shù)，圖象應(yīng)是上升的，由上述分析，可知選C.【答案】C2設(shè)f(x)，g(x)在a，b上可導(dǎo)，且f(x)g(x)，則當axb時，有() 【導(dǎo)學(xué)號：26160085】Af(x)g(x)Bf(x)g(x)Cf(x)g(a)g(x)f(a)Df(x)g(b)g(x)f(b)【解析】f(x)g(x)0，(f(x)g(x)0，f(x)g(x)在a，b上是增函數(shù)，當axb時，

8、f(x)g(x)f(a)g(a)，f(x)g(a)g(x)f(a)故選C.【答案】C3若函數(shù)f(x)ln xax22x存在單調(diào)遞減區(qū)間，則實數(shù)a的取值范圍是_【解析】f(x)ax2.因為函數(shù)f(x)存在單調(diào)遞減區(qū)間，所以f(x)0有解又因為函數(shù)f(x)的定義域為(0，)所以ax22x10在(0，)內(nèi)有解當a>0時，yax22x1為開口向上的拋物線，ax22x10在(0，)內(nèi)恒有解；當a<0時，yax22x1為開口向下的拋物線，若ax22x10在(0，)內(nèi)恒有解，則解得1a<0；當a0時，顯然符合題意綜合上述，a的取值范圍是1，)【答案】1，)4已知函數(shù)f(x)x3ax1.(1

9、)若f(x)在R上單調(diào)遞增，求a的取值范圍；(2)是否存在實數(shù)a，使f(x)在(1,1)上單調(diào)遞減？若存在，求出a的取值范圍；若不存在，說明理由；(3)證明：f(x)x3ax1的圖象不可能總在直線ya的上方【解】(1)f(x)3x2a，3x2a0在R上恒成立，即a3x2在R上恒成立，又y3x20，當a0時，f(x)x3ax1在R上是增函數(shù)，又a0時，f(x)3x2不恒為0，a0.(2)3x2a0在(1,1)上恒成立，a3x2在(1，1)上恒成立但當x(1，1)時，03x2<3，a3，即當a3時，f(x)在(1,1)上單調(diào)遞減(3)證明：取x1，得f(1)a2<a，即存在點(1，a2)在f(x)x3ax1的圖象上，且在直線ya 的下方