（河北專版）2018年秋八年級數(shù)學(xué)上冊 第十二章 全等三角形檢測題 （新版）新人教版

《（河北專版）2018年秋八年級數(shù)學(xué)上冊 第十二章 全等三角形檢測題 （新版）新人教版》由會員分享，可在線閱讀，更多相關(guān)《（河北專版）2018年秋八年級數(shù)學(xué)上冊 第十二章 全等三角形檢測題 （新版）新人教版（7頁珍藏版）》請在裝配圖網(wǎng)上搜索。

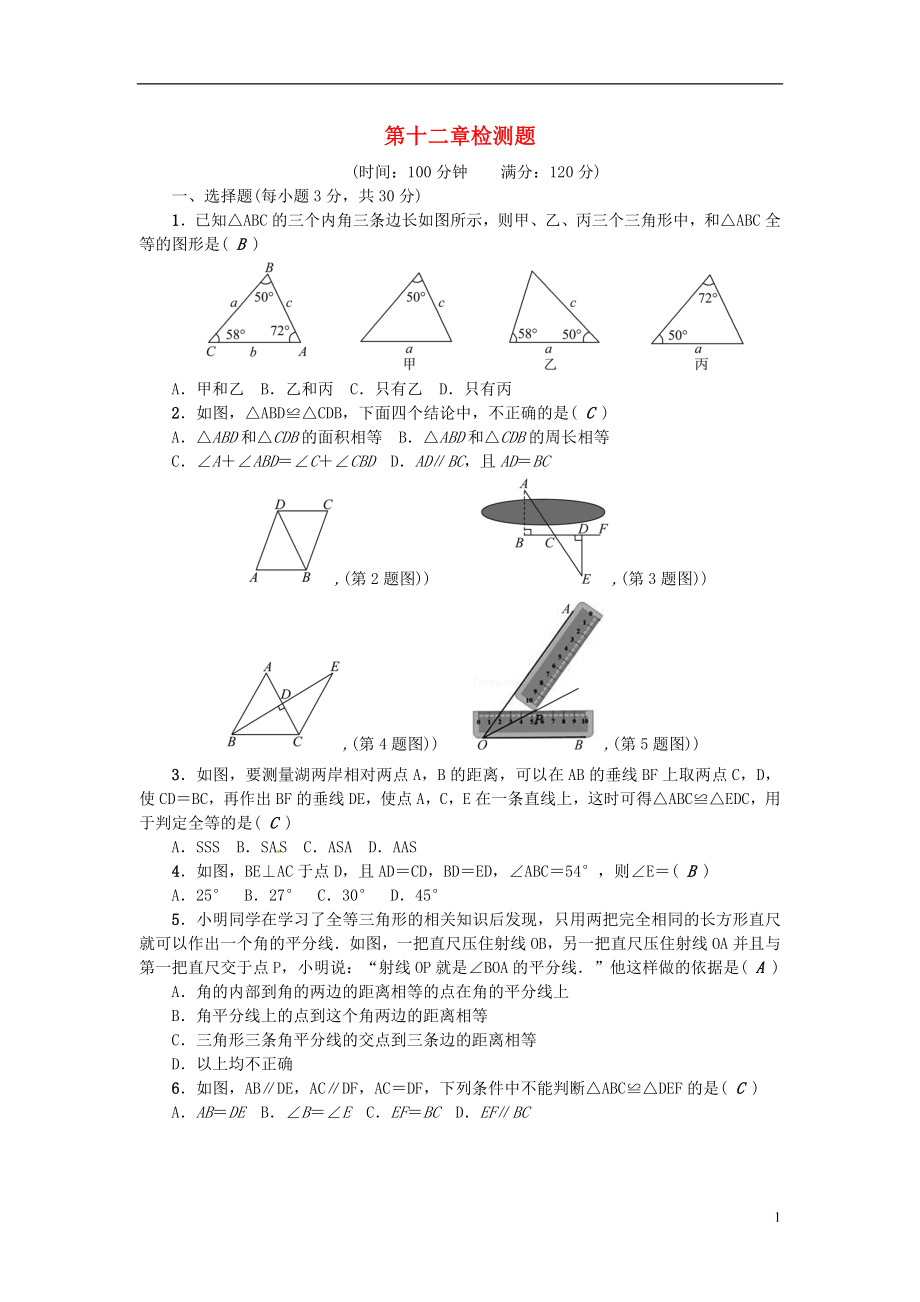
1、 第十二章檢測題 (時間：100分鐘　　滿分：120分) 一、選擇題(每小題3分，共30分) 1．已知△ABC的三個內(nèi)角三條邊長如圖所示，則甲、乙、丙三個三角形中，和△ABC全等的圖形是( B ) A．甲和乙 B．乙和丙 C．只有乙 D．只有丙 2．如圖，△ABD≌△CDB，下面四個結(jié)論中，不正確的是( C ) A．△ABD和△CDB的面積相等 B．△ABD和△CDB的周長相等 C．∠A＋∠ABD＝∠C＋∠CBD D．AD∥BC，且AD＝BC ,(第2題圖))　　　,(第3題圖))　　,(第4題圖))　　,(第5題圖)) 3．如圖，要測量湖兩岸相對兩點A，B的

2、距離，可以在AB的垂線BF上取兩點C，D，使CD＝BC，再作出BF的垂線DE，使點A，C，E在一條直線上，這時可得△ABC≌△EDC，用于判定全等的是( C ) A．SSS B．SAS C．ASA D．AAS 4．如圖，BE⊥AC于點D，且AD＝CD，BD＝ED，∠ABC＝54°，則∠E＝( B ) A．25° B．27° C．30° D．45° 5．小明同學(xué)在學(xué)習(xí)了全等三角形的相關(guān)知識后發(fā)現(xiàn)，只用兩把完全相同的長方形直尺就可以作出一個角的平分線．如圖，一把直尺壓住射線OB，另一把直尺壓住射線OA并且與第一把直尺交于點P，小明說：“射線OP就是∠BOA的平分線．”他這樣做的

3、依據(jù)是( A ) A．角的內(nèi)部到角的兩邊的距離相等的點在角的平分線上 B．角平分線上的點到這個角兩邊的距離相等 C．三角形三條角平分線的交點到三條邊的距離相等 D．以上均不正確 6．如圖，AB∥DE，AC∥DF，AC＝DF，下列條件中不能判斷△ABC≌△DEF的是( C ) A．AB＝DE B．∠B＝∠E C．EF＝BC D．EF∥BC ,(第6題圖))　　,(第7題圖))　　,(第8題圖))　　,(第9題圖)) 7．如圖，已知AB＝DC，AD＝BC，E，F(xiàn)是DB上兩點且BF＝DE，若∠AEB＝100°，∠ADB＝30°，則∠BCF＝( D ) A．150° B．40

4、° C．80° D．70° 8．如圖，AB⊥BC，BE⊥AC，∠1＝∠2，AD＝AB，則( D ) A．∠1＝∠EFD B．BE＝EC C．BF＝DF＝CD D．FD∥BC 9．如圖，在△ABC中，AB＝AC，點E，F(xiàn)是中線AD上的兩點，則圖中可證明為全等三角形的有( D ) A．3對 B．4對 C．5對 D．6對 10．如圖，在△ABC中，AB＝AC，AD是角平分線，BE＝CF，則下列說法正確的個數(shù)是( D ) ①AD平分∠EDF；②△EBD≌△FCD；③BD＝CD；④AD⊥BC. A．1 B．2 C．3 D．4 ,(第10題圖))　　,(第11題圖))

5、　　,(第12題圖))　　,(第13題圖)) 二、填空題(每小題3分，共24分) 11．如圖，△ABC≌△DEF，且△ABC的周長為11，若AB＝3，EF＝5，則AC＝3． 12．如圖，已知點A，B，D，E在同一直線上，AD＝EB，BC∥DF，要使△ABC≌△EDF，則要添加的一個條件是∠A＝∠E(答案不唯一)．(只需填寫一個即可) 13．如圖，已知△ABE≌△ACF，∠E＝∠F＝90°，∠CMD＝70°，則∠2＝20 度． 14．如圖，AB＝AC，AD＝AE，∠BAC＝∠DAE，∠1＝25°，∠2＝30°，則∠3＝55°． ,(第14題圖))　　,(第15題圖))　　,(第16題

6、圖))　　,(第17題圖)) 15．如圖，△ABC的周長為32，且AB＝AC，AD⊥BC于點D，△ACD的周長為24，那么AD的長為8． 16．如圖，旗桿AC與旗桿BD相距12 m，某人從點B沿BA走向點A，一段時間后他到達點M，此時他仰望旗桿的頂點C和D，兩次視線的夾角為90°，且CM＝DM.已知旗桿AC的高為3 m，該人的運動速度為1 m/s，則這個人運動到點M所用時間是3s. 17．如圖，O是直線BC上的點，OM平分∠AOB，ON平分∠AOC，點E在OM上，過點E作EG⊥OA于點G，EP⊥OB于點P，延長EG，交ON于點F，過點F作FQ⊥OC于點Q，若EF＝10，則FQ＋EP的長度

7、為10． 18．如圖，AC＝AE，AD＝AB，∠ACB＝∠DAB＝90°，∠BAE＝35°，AE∥CB，AC，DE交于點F. (1)∠DAC＝35度； (2)猜想線段AF與BC的數(shù)量關(guān)系是BC＝2AF． 三、解答題(共66分) 19．(8分)如圖，點D為碼頭，A，B兩個燈塔與碼頭的距離相等，DA，DB為海岸線．一輪船離開碼頭，計劃沿∠ADB的平分線航行，在航行途中C點處測得輪船與燈塔A和燈塔B的距離相等．試問：輪船航行是否偏離指定航線？請說明理由． 解：此時輪船沒有偏離航線．理由：由題意，知DA＝DB，AC＝BC，在△ADC和△BDC中，∴△ADC≌△BDC(SSS)，∴∠

8、ADC＝∠BDC，即DC為∠ADB的平分線，∴此時輪船沒有偏離航線． 20．(8分)如圖，AB∥CD. (1)用直尺和圓規(guī)作∠C的平分線CP，CP交AB于點E；(保留作圖痕跡，不寫作法) (2)在(1)中作出的線段CE上取一點F，連接AF，要使△ACF≌△AEF，還需要添加一個什么條件？請你寫出這個條件．(只要給出一種情況即可；圖中不再增加字母和線段；不要求證明) 解：(1)作圖略． (2)AF⊥CE或∠CAF＝∠EAF等． 21．(10分)如圖，已知△ABC中，∠1＝∠2，AE＝AD，求證：DF＝EF. 證明：在△ABE和△ACD中，∴△ABE≌△ACD

9、(AAS)，∴AB＝AC，∵AE＝AD，∴AB－AD＝AC－AE，即BD＝CE，在△BDF和△CEF中，∴△BDF≌△CEF(AAS)，∴DF＝EF. 22．(12分)如圖，在Rt△ABC中，AB＝AC，∠BAC＝90°，BD平分∠ABC交AC于點D，CE⊥BD交BD的延長線于點E，則線段BD和CE具有什么數(shù)量關(guān)系？證明你的結(jié)論． 解： BD＝2CE.證明：如圖，延長CE與BA的延長線交于點F，∵∠BAC＝90°，CE⊥BD，∴∠BAC＝∠DEC，∵∠ADB＝∠CDE，∴∠ABD＝∠DCE，在△BAD和△CAF中，∴△BAD≌△CAF(ASA)，∴BD＝CF，∵BD平分∠AB

10、C，CE⊥DB，∴∠FBE＝∠CBE，在△BEF和△BEC中，∴△BEF≌△BEC(ASA)，∴CE＝EF，∴DB＝2CE. 23．(14分)如圖，已知△ABC中，AB＝AC＝10 cm，BC＝8 cm，點D為AB的中點．如果點P在線段BC上以3 cm/s的速度由點B向點C運動，同時，點Q在線段CA上由點C向點A運動． (1)若點Q與點P的運動速度相等，經(jīng)過1秒后，△BPD與△CQP是否全等？請說明理由； (2)若點Q與點P的運動速度不相等，當點Q的運動速度為多少時，能使△BPD與△CQP全等？ 解：(1)全等．理由如下：∵△ABC中，AB＝AC，∴∠B＝∠C，由題意可知，

11、BD＝AB＝5 cm，經(jīng)過1秒后，PB＝3 cm，PC＝5 cm，CQ＝3 cm，在△BPD和△CQP中，∴△BPD≌△CQP(SAS)．(2)設(shè)點Q的運動速度為x(x≠3)cm/s，經(jīng)過t s△BPD與△CQP全等，則可知PB＝3t cm，PC＝(8－3t) cm，CQ＝xt cm，∵AB＝AC，∴∠B＝∠C，根據(jù)全等三角形的判定定理SAS可知，有兩種情況：①當BD＝PC，BP＝CQ時，8－3t＝5且3t＝xt，解得t＝1，x＝3，∵x≠3，∴舍去此情況；②當BD＝CQ，BP＝PC時，5＝xt且3t＝8－3t，解得t＝，x＝.故若點Q與點P的運動速度不相等，當點Q的運動速度為 cm/s時，能

12、使△BPD與△CQP全等． 24．(14分)【問題提出】學(xué)習(xí)了三角形全等的判定方法(即“SAS”“ASA”“AAS”“SSS”)和直角三角形全等的判定方法(即“HL”)后，我們繼續(xù)對“兩個三角形滿足兩邊和其中一邊的對角對應(yīng)相等”的情形進行研究． 【初步思考】我們不妨將問題用符號語言表示為：在△ABC和△DEF中，AC＝DF，BC＝EF，∠B＝∠E，然后，對∠B進行分類，可分為“∠B是直角、鈍角、銳角”三種情況進行探究． 【深入探究】 第一種情況：當∠B是直角時，△ABC≌△DEF. (1)如圖①，在△ABC和△DEF中，AC＝DF，BC＝EF，∠B＝∠E＝90°，根據(jù)HL，可以知

13、道Rt△ABC≌Rt△DEF. 第二種情況：當∠B是鈍角時，△ABC≌△DEF. (2)如圖②，在△ABC和△DEF中，AC＝DF，BC＝EF，∠B＝∠E，且∠B，∠E都是鈍角，求證：△ABC≌△DEF. 第三種情況：當∠B是銳角時，△ABC和△DEF不一定全等． (3)在△ABC和△DEF中，AC＝DF，BC＝EF，∠B＝∠E，且∠B，∠E都是銳角，請你用尺規(guī)在圖③中作出△DEF，使△DEF和△ABC不全等．(不寫作法，保留作圖痕跡) (4)在(3)中，∠B還要滿足什么條件，就可以使△ABC≌△DEF？請直接寫出結(jié)論：在△ABC和△DEF中，AC＝DF，BC＝EF，∠B＝∠E，且∠B，∠E都是銳角，若∠B≥∠A，則△ABC≌△DEF. 解：(1)HL　(2)證明：過點C作CG⊥AB交AB的延長線于點G，過點F作FH⊥DE交DE的延長線于點H(圖略)，∵∠ABC＝∠DEF，且∠ABC，∠DEF都是鈍角，∴180°－∠ABC＝180°－∠DEF，即∠CBG＝∠FEH，在△CBG和△FEH中，∴△CBG≌△FEH(AAS)，∴CG＝FH，在Rt△ACG和Rt△DFH中，∴Rt△ACG≌Rt△DFH(HL)，∴∠A＝∠D，在△ABC和△DEF中，∴△ABC≌△DEF(AAS)． (3)如圖，△DEF和△ABC不全等．(4)∠B≥∠A 7