《【志鴻優(yōu)化設(shè)計(jì)】高考數(shù)學(xué)文科人教版二輪專題升級(jí)訓(xùn)練:專題七 概率與統(tǒng)計(jì)含答案解析》由會(huì)員分享��,可在線閱讀���,更多相關(guān)《【志鴻優(yōu)化設(shè)計(jì)】高考數(shù)學(xué)文科人教版二輪專題升級(jí)訓(xùn)練:專題七 概率與統(tǒng)計(jì)含答案解析(4頁珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索�����。
1����、專題升級(jí)訓(xùn)練 概率與統(tǒng)計(jì)
(時(shí)間:60分鐘 滿分:100分)
一、選擇題(本大題共6小題,每小題6分,共36分)
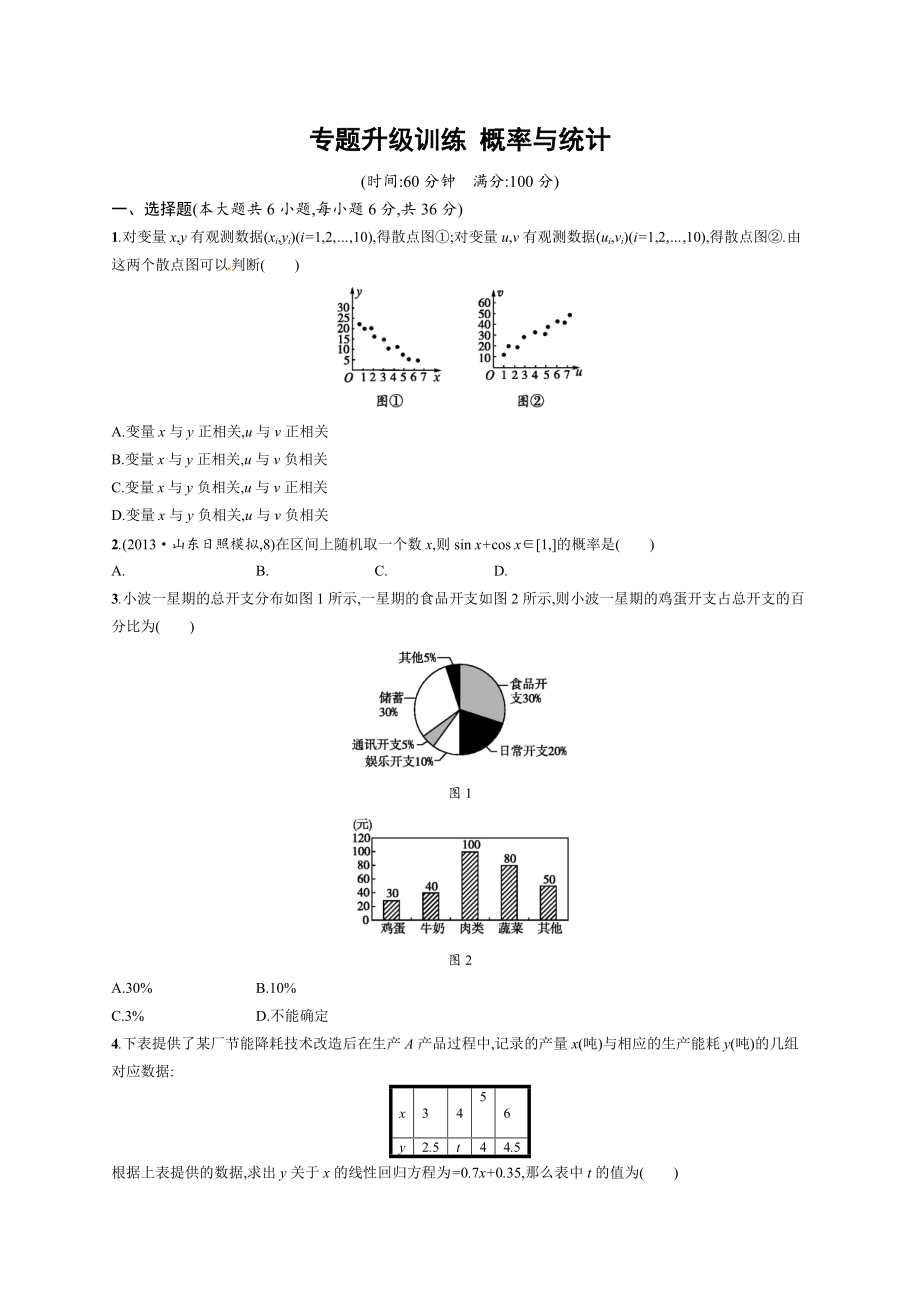
1.對(duì)變量x,y有觀測(cè)數(shù)據(jù)(xi,yi)(i=1,2,…,10),得散點(diǎn)圖①;對(duì)變量u,v有觀測(cè)數(shù)據(jù)(ui,vi)(i=1,2,…,10),得散點(diǎn)圖②.由這兩個(gè)散點(diǎn)圖可以判斷( )
A.變量x與y正相關(guān),u與v正相關(guān)
B.變量x與y正相關(guān),u與v負(fù)相關(guān)
C.變量x與y負(fù)相關(guān),u與v正相關(guān)
D.變量x與y負(fù)相關(guān),u與v負(fù)相關(guān)
2.(2013山東日照模擬,8)在區(qū)間上隨機(jī)取一個(gè)數(shù)x,則sin x+cos x∈[1,]的概率是( )
A. B. C. D.
2���、3.小波一星期的總開支分布如圖1所示,一星期的食品開支如圖2所示,則小波一星期的雞蛋開支占總開支的百分比為( )
圖1
圖2
A.30% B.10%
C.3% D.不能確定
4.下表提供了某廠節(jié)能降耗技術(shù)改造后在生產(chǎn)A產(chǎn)品過程中,記錄的產(chǎn)量x(噸)與相應(yīng)的生產(chǎn)能耗y(噸)的幾組對(duì)應(yīng)數(shù)據(jù):
x
3
4
5[來源:]
6
y
2.5
t
4
4.5
根據(jù)上表提供的數(shù)據(jù),求出y關(guān)于x的線性回歸方程為=0.7x+0.35,那么表中t的值為( )
A.3 B.3.15 C.3.5 D.4.5
5.一個(gè)盒子中裝有4張卡片,上面分別寫著如下四個(gè)定義域?yàn)镽的函數(shù)
3���、:f1(x)=x3,f2(x)=|x|,f3(x)=sin x,f4(x)=cos x,現(xiàn)從盒子中任取2張卡片,將卡片上的函數(shù)相乘得到一個(gè)新函數(shù),所得函數(shù)為奇函數(shù)的概率是( )
A. B. C. D.
6.甲、乙兩名運(yùn)動(dòng)員在某項(xiàng)測(cè)試中的6次成績(jī)?nèi)缜o葉圖所示,分別表示甲���、乙兩名運(yùn)動(dòng)員這項(xiàng)測(cè)試成績(jī)的平均數(shù),s1,s2分別表示甲���、乙兩名運(yùn)動(dòng)員這項(xiàng)測(cè)試成績(jī)的標(biāo)準(zhǔn)差,則有( )
A.,s1s2
二、填空題(本大題共3小題,每小題6分,共18分)
7.一支田徑運(yùn)動(dòng)隊(duì)有男運(yùn)動(dòng)員56人,女運(yùn)動(dòng)員42人.現(xiàn)用分層抽樣的方法抽取若干人,若
4�����、抽取的男運(yùn)動(dòng)員有8人,則抽取的女運(yùn)動(dòng)員有 人.
8.從{1,2,3,4,5,6}中隨機(jī)選一個(gè)數(shù)a,從{1,2,3}中隨機(jī)選一個(gè)數(shù)b,則a
5�����、[來源:]
(1)求圖中a的值;
(2)根據(jù)頻率分布直方圖,估計(jì)這100名學(xué)生語文成績(jī)的平均數(shù);
(3)若這100名學(xué)生語文成績(jī)某些分?jǐn)?shù)段的人數(shù)(x)與數(shù)學(xué)成績(jī)相應(yīng)分?jǐn)?shù)段的人數(shù)(y)之比如下表所示,求數(shù)學(xué)成績(jī)?cè)赱50,90)之外的人數(shù).
分?jǐn)?shù)段
[50,60)
[60,70)
[70,80)
[80,90)
x∶y
1∶1
2∶1
3∶4
4∶5
11.(本小題滿分15分)某花店每天以每枝5元的價(jià)格從農(nóng)場(chǎng)購進(jìn)若干枝玫瑰花,然后以每枝10元的價(jià)格出售.如果當(dāng)天賣不完,剩下的玫瑰花做垃圾處理.
(1)若花店一天購進(jìn)17枝玫瑰花,求當(dāng)天的利潤(rùn)y(單位:元)關(guān)于當(dāng)天需
6、求量n(單位:枝,n∈N)的函數(shù)解析式;
(2)花店記錄了100天玫瑰花的日需求量(單位:枝),整理得下表:
日需求量n
14
15
16
17
18
19
20
頻數(shù)
10
20
16
16
15
13
10
①假設(shè)花店在這100天內(nèi)每天購進(jìn)17枝玫瑰花,求這100天的日利潤(rùn)(單位:元)的平均數(shù);
②若花店一天購進(jìn)17枝玫瑰花,以100天記錄的各需求量的頻率作為各需求量發(fā)生的概率,求當(dāng)天的利潤(rùn)不少于75元的概率.
12.(本小題滿分16分)(2013廣東深圳模擬,17)2013年3月14日,CCTV財(cái)經(jīng)頻道報(bào)道了某地建筑市場(chǎng)存在違規(guī)使用未經(jīng)淡化海砂的現(xiàn)
7��、象.為了研究使用淡化海砂與混凝土耐久性是否達(dá)標(biāo)有關(guān),某大學(xué)實(shí)驗(yàn)室隨機(jī)抽取了60個(gè)樣本,得到了相關(guān)數(shù)據(jù)如下表:
混凝土
耐久性達(dá)標(biāo)
混凝土
耐久性不達(dá)標(biāo)
總計(jì)
使用淡化海砂
25
5
30
使用未經(jīng)
淡化海砂
15
15
30
總計(jì)[來源:數(shù)理化網(wǎng)]
40
20
60
(1)根據(jù)表中數(shù)據(jù),利用獨(dú)立性檢驗(yàn)的方法判斷,能否在犯錯(cuò)誤的概率不超過1%的前提下,認(rèn)為使用淡化海砂與混凝土耐久性是否達(dá)標(biāo)有關(guān)?
(2)若用分層抽樣的方法在使用淡化海砂的樣本中抽取了6個(gè),現(xiàn)從這6個(gè)樣本中任取2個(gè),則取出的2個(gè)樣本混凝土耐久性都達(dá)標(biāo)的概率是多少?
參考數(shù)據(jù):K2=
P
8����、(K2≥k)
0.100
0.050
0.025
0.010
0.001
k
2.706
3.841
5.024
6.635
10.828
##
一、選擇題(本大題共6小題,每小題6分,共36分)
1.C 解析:題圖①的散點(diǎn)分布在斜率小于0的直線附近,y隨x的增大而減小,故變量x與y負(fù)相關(guān).
題圖②的散點(diǎn)分布在斜率大于0的直線附近,v隨u的增大而增大,故變量u與v正相關(guān),選C.
2.B 解析:在中滿足sin x+cos x∈[1,]的數(shù)x的范圍為x∈,[來源:數(shù)理化網(wǎng)]
∴P=.
3.C 解析:由題圖2知,小波一星期的食品開支為300元,其中雞蛋開支為30元
9���、,占食品開支的10%,而食品開支占總開支的30%,所以小波一星期的雞蛋開支占總開支的百分比為3%,故選C.
4.A 解析:由題意知,,又因?yàn)榫€性回歸直線=0.7x+0.35恒過()點(diǎn),可得t=3,故選A.
5.C 解析:f1(x)與f3(x)是奇函數(shù),f2(x)與f4(x)是偶函數(shù).奇函數(shù)與偶函數(shù)相乘是奇函數(shù),
故所得函數(shù)為奇函數(shù)的概率是P=.
6.B 解析:依題意,得(9+14+152+16+21)=15,(8+13+152+17+22)=15,[(9-15)2+(14-15)2+2(15-15)2+(16-15)2+(21-15)2]≈12.3,[(8-15)2+(13-15)2+
10��、2(15-15)2+(17-15)2+(22-15)2]≈17.7,,即s1
11���、應(yīng)寫出必要的文字說明�����、證明過程或演算步驟)
10.解:(1)依題意,得10(2a+0.02+0.03+0.04)=1,解得a=0.005.
(2)這100名學(xué)生語文成績(jī)的平均數(shù)為550.05+650.4+750.3+850.2+950.05=73.
(3)數(shù)學(xué)成績(jī)?cè)赱50,60)的人數(shù)為1000.05=5,數(shù)學(xué)成績(jī)?cè)赱60,70)的人數(shù)為1000.4=20,數(shù)學(xué)成績(jī)?cè)赱70,80)的人數(shù)為1000.3=40,數(shù)學(xué)成績(jī)?cè)赱80,90)的人數(shù)為1000.2=25,所以數(shù)學(xué)成績(jī)?cè)赱50,90)之外的人數(shù)為100-5-20-40-25=10.[來源:]
11.解:(1)當(dāng)日需求量n≥17時(shí),利
12��、潤(rùn)y=85.
當(dāng)日需求量n<17時(shí),利潤(rùn)y=10n-85.
所以y關(guān)于n的函數(shù)解析式為y=(n∈N).
(2)①這100天中有10天的日利潤(rùn)為55元,20天的日利潤(rùn)為65元,16天的日利潤(rùn)為75元,54天的日利潤(rùn)為85元,所以這100天的日利潤(rùn)的平均數(shù)為(5510+6520+7516+8554)=76.4(元).
②利潤(rùn)不低于75元當(dāng)且僅當(dāng)日需求量不少于16枝.故當(dāng)天的利潤(rùn)不少于75元的概率為
P=0.16+0.16+0.15+0.13+0.1=0.7.
12.解:(1)提出假設(shè)H0:使用淡化海砂與混凝土耐久性是否達(dá)標(biāo)無關(guān),
根據(jù)表中數(shù)據(jù),求得
K2==7.5>6.635,
13����、查表得P(K2≥6.635)=0.010,
∴能在犯錯(cuò)誤的概率不超過1%的前提下,認(rèn)為使用淡化海砂與混凝土耐久性是否達(dá)標(biāo)有關(guān).
(2)用分層抽樣的方法在使用淡化海砂的樣本中抽取6個(gè),其中抽取“混凝土耐久性達(dá)標(biāo)”的為6=5(個(gè)),“混凝土耐久性不達(dá)標(biāo)”的為6-5=1(個(gè)).
“混凝土耐久性達(dá)標(biāo)”記為A1,A2,A3,A4,A5,“混凝土耐久性不達(dá)標(biāo)”記為B.
在這6個(gè)樣本中任取2個(gè),有以下幾種可能:(A1,A2),(A1,A3),(A1,A4),(A1,A5),(A1,B),(A2,A3),(A2,A4),(A2,A5),(A2,B),(A3,A4),(A3,A5),(A3,B),(A4,A5),(A4,B),(A5,B),共15種.
設(shè)“取出的2個(gè)樣本混凝土耐久性都達(dá)標(biāo)”為事件A,它的對(duì)立事件為“取出的2個(gè)樣本至少有1個(gè)混凝土耐久性不達(dá)標(biāo)”,包含(A1,B),(A2,B),(A3,B),(A4,B),(A5,B),共5種可能,
∴P(A)=1-P()=1-,
即取出的2個(gè)樣本混凝土耐久性都達(dá)標(biāo)的概率是.
 【志鴻優(yōu)化設(shè)計(jì)】高考數(shù)學(xué)文科人教版二輪專題升級(jí)訓(xùn)練:專題七 概率與統(tǒng)計(jì)含答案解析
【志鴻優(yōu)化設(shè)計(jì)】高考數(shù)學(xué)文科人教版二輪專題升級(jí)訓(xùn)練:專題七 概率與統(tǒng)計(jì)含答案解析