《高三數(shù)學二輪復習 第1部分 專題3 突破點6 古典概型與幾何概型 理-人教高三數(shù)學試題》由會員分享����,可在線閱讀,更多相關(guān)《高三數(shù)學二輪復習 第1部分 專題3 突破點6 古典概型與幾何概型 理-人教高三數(shù)學試題(8頁珍藏版)》請在裝配圖網(wǎng)上搜索���。
1��、專題三 概率與統(tǒng)計
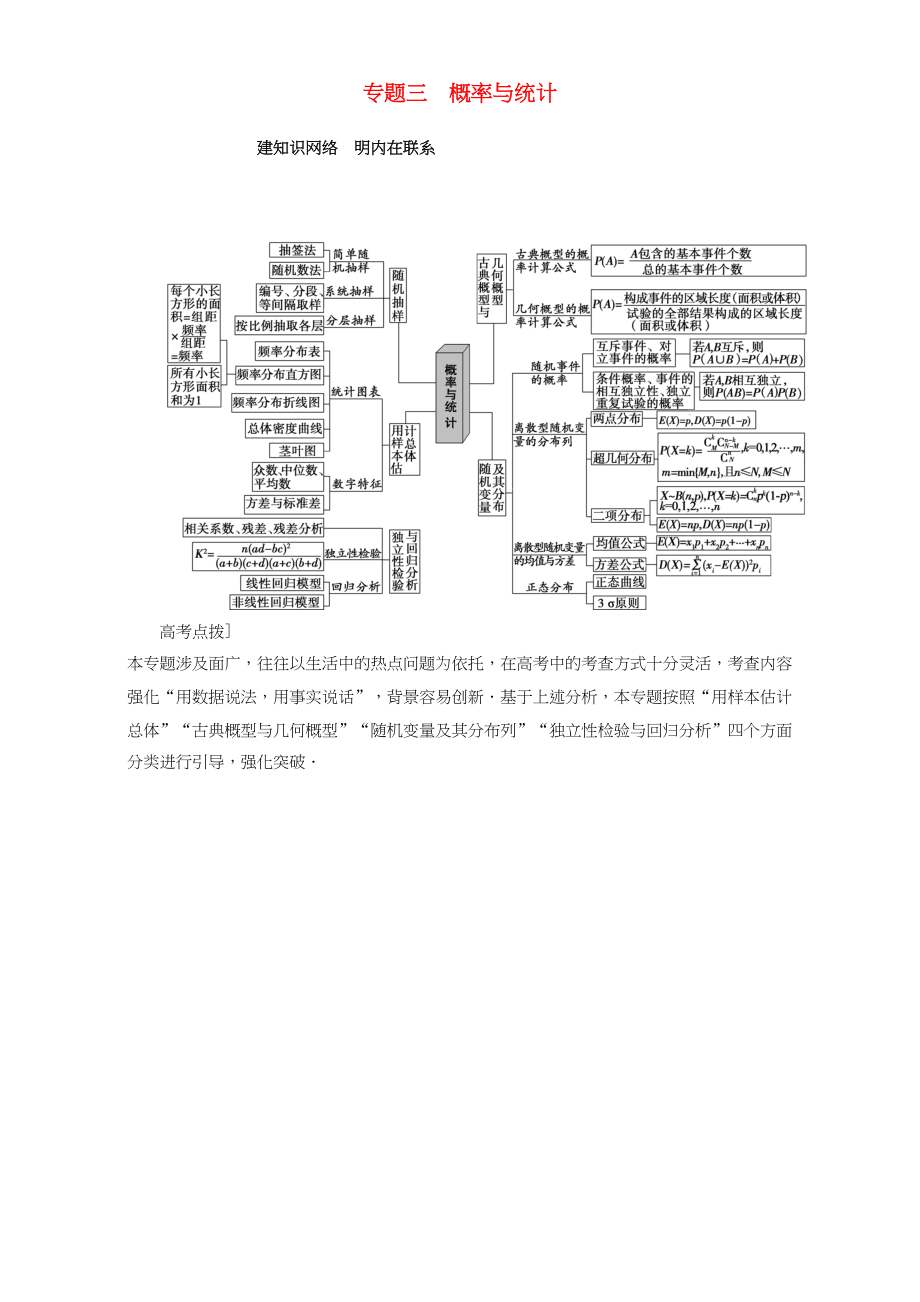
建知識網(wǎng)絡(luò) 明內(nèi)在聯(lián)系
高考點撥] 本專題涉及面廣���,往往以生活中的熱點問題為依托����,在高考中的考查方式十分靈活��,考查內(nèi)容強化“用數(shù)據(jù)說法�����,用事實說話”�,背景容易創(chuàng)新.基于上述分析,本專題按照“用樣本估計總體”“古典概型與幾何概型”“隨機變量及其分布列”“獨立性檢驗與回歸分析”四個方面分類進行引導�,強化突破.
突破點6 古典概型與幾何概型
提煉1
古典概型問題的求解技巧
(1)直接列舉:涉及一些常見的古典概型問題時,往往把事件發(fā)生的所有結(jié)果逐一列舉出來���,然后進行求解.
(2)畫樹狀圖:涉及一些特殊古典概型問題時����,直接列舉容易出
2��、錯�����,通過畫樹狀圖,列舉過程更具有直觀性���、條理性���,使列舉結(jié)果不重、不漏.
(3)逆向思維:對于較復雜的古典概型問題�����,若直接求解比較困難�,可利用逆向思維,先求其對立事件的概率��,進而可得所求事件的概率.
(4)活用對稱:對于一些具有一定對稱性的古典概型問題�����,通過列舉基本事件個數(shù)結(jié)合古典概型的概率公式來處理反而比較復雜���,利用對稱思維,可以快速解決.
提煉2
幾何度量法求解幾何概型
準確確定度量方式和度量公式是求解幾何概型的關(guān)鍵����,常見的幾何度量涉及的測度主要包括長度�����、面積��、體積�����、角度等.
提煉3
求概率的兩種常用方法
(1)將所求事件轉(zhuǎn)化成幾個彼此互斥的事件的和事件����,利用概率加法公式求解
3��、概率.
(2)若一個較復雜的事件的對立面的分類較少����,可考慮利用對立事件的概率公式,即“正難則反”.它常用來求“至少”或“至多”型事件的概率.
回訪1 古典概型
1.(2014·全國卷Ⅰ)4位同學各自在周六�、周日兩天中任選一天參加公益活動,則周六��、周日都有同學參加公益活動的概率為( )
A. B.
C. D.
D 4名同學各自在周六、周日兩天中任選一天參加公益活動的情況有24=16(種)��,其中僅在周六(周日)參加的各有1種��,
∴所求概率為1-=.]
2.(2013·全國卷Ⅱ)從n個正整數(shù)1,2��,…��,n中任意取出兩個不同的數(shù)�,若取出的兩數(shù)之和等于5的概率為,則n=_
4��、_______.
8 由題意知n>4���,取出的兩數(shù)之和等于5的有兩種情況:1,4和2,3��,所以P==���,即n2-n-56=0,解得n=-7(舍去)或n=8.]
回訪2 幾何概型
3.(2016·全國乙卷)某公司的班車在7:30,8:00,8:30發(fā)車�,小明在7:50至8:30之間到達發(fā)車站乘坐班車,且到達發(fā)車站的時刻是隨機的���,則他等車時間不超過10分鐘的概率是( )
A. B.
C. D.
B 如圖,7:50至8:30之間的時間長度為40分鐘����,而小明等車時間不超過10分鐘是指小明在7:50至8:00之間或8:20至8:30之間到達發(fā)車站�����,此兩種情況下的時間長度之和為
5���、20分鐘,由幾何概型概率公式知所求概率為P==.故選B.]
4.(2016·全國甲卷)從區(qū)間0,1]隨機抽取2n個數(shù)x1��,x2�,…,xn�����,y1�,y2,…��,yn����,構(gòu)成n個數(shù)對(x1,y1),(x2�,y2),…����,(xn,yn)�,其中兩數(shù)的平方和小于1的數(shù)對共有m個,則用隨機模擬的方法得到的圓周率π的近似值為( )
A. B.
C. D.
C 因為x1��,x2��,…����,xn,y1��,y2��,…��,yn都在區(qū)間0,1]內(nèi)隨機抽取�����,所以構(gòu)成的n個數(shù)對(x1,y1)���,(x2,y2)���,…���,(xn,yn)都在正方形OABC內(nèi)(包括邊界)�����,如圖所示.若兩數(shù)的平方和小于1�����,則對應(yīng)的數(shù)對在扇形OAC內(nèi)(不包括
6����、扇形圓弧上的點所對應(yīng)的數(shù)對),故在扇形OAC內(nèi)的數(shù)對有m個.用隨機模擬的方法可得=��,即=��,所以π=.]
熱點題型1 古典概型
題型分析:古典概型是高考考查概率的核心,問題背景大多是取球��、選人�、組數(shù)等,求解的關(guān)鍵是準確列舉基本事件�,難度較小.
(1)一個袋子中有5個大小相同的球,其中3個白球與2個黑球���,先從袋中任意取出一個球�,取出后不放回���,然后從袋中任意取出一個球�,則第一次為白球��、第二次為黑球的概率為( )
A. B.
C. D.
(2)已知M={1,2,3,4}��,若a∈M��,b∈M���,則函數(shù)f(x)=ax3+bx2+x-3在R上為增函數(shù)的概率是( )
【導
7�、學號:85952027】
A. B.
C. D.
(1)B (2)A (1)設(shè)3個白球分別為a1�����,a2,a3,2個黑球分別為b1����,b2,則先后從中取出2個球的所有可能結(jié)果為(a1���,a2),(a1���,a3)���,(a1,b1)�,(a1,b2)���,(a2�,a3)���,(a2���,b1)���,(a2,b2)��,(a3���,b1)�,(a3���,b2)��,(b1�����,b2)���,(a2,a1)���,(a3�����,a1)����,(b1,a1)��,(b2��,a1)�,(a3��,a2)��,(b1�,a2),(b2��,a2)����,(b1,a3)�����,(b2,a3)��,(b2��,b1)�,共20種.
其中滿足第一次為白球、第二次為黑球的有(a1����,b1),(a1����,b2),(a2�����,b1)
8、��,(a2���,b2)��,(a3�,b1)�,(a3�,b2),共6種��,故所求概率為=.故選B.
(2)記事件A為“函數(shù)f(x)=ax3+bx2+x-3在R上為增函數(shù)”.
因為f(x)=ax3+bx2+x-3��,所以f′(x)=3ax2+2bx+1.
因為函數(shù)f(x)在R上為增函數(shù)���,所以f′(x)≥0在R上恒成立.
又a>0,所以Δ=(2b)2-4×3a=4b2-12a≤0在R上恒成立��,即a≥.
所以當b=1時�����,有a≥,故a可取1,2,3,4��,共4個數(shù)���;
當b=2時��,有a≥���,故a可取2,3,4,共3個數(shù)�����;
當b=3時��,有a≥3��,故a可取3,4�����,共2個數(shù)�;
當b=4時,有a≥,故a無可取值.
9��、綜上���,事件A包含的基本事件有4+3+2=9(種).
又a���,b∈{1,2,3,4},所以(a���,b)共有4×4=16(種).
故所求事件A的概率為P(A)=.故選A.]
利用古典概型求事件概率的關(guān)鍵及注意點
1.關(guān)鍵:正確列舉出基本事件的總數(shù)和待求事件包括的基本事件數(shù).
2.注意點:(1)對于較復雜的題目��,列出事件數(shù)時要正確分類����,分類時應(yīng)不重不漏.
(2)當直接求解有困難時�,可考慮求其對立事件的概率.
變式訓練1] (2016·廣州二模)從數(shù)字1,2,3,4,5中任取2個,組成一個沒有重復數(shù)字的兩位數(shù)�����,則這個兩位數(shù)大于30的概率是( )
A. B.
C. D.
C 從
10���、數(shù)字1,2,3,4,5中任取2個,組成一個沒有重復數(shù)字的兩位數(shù),共有20種不同結(jié)果.其中這個兩位數(shù)大于30的共有12種不同結(jié)果��,故所求事件的概率P==.]
熱點題型2 幾何概型
題型分析:高考試題中幾何概型主要考查線段型和面積型.求解幾何概型的關(guān)鍵是計算線段的長度��、平面圖形的面積等�,難度較小.
(1)在區(qū)間0,2]上隨機地取一個數(shù)x,則事件“-1≤log≤1”發(fā)生的概率為( )
A. B.
C. D.
(2)某校早上8:00開始上課���,假設(shè)該校學生小張與小王在早上7:30~7:50之間到校���,且每人在該時間段的任何時刻到校是等可能的,則小張比小王至少早5分鐘到校的概率為__
11���、________.(用數(shù)字作答)
(1)A (2) (1)由-1≤log≤1��,得≤x+≤2��,解得0≤x≤���,所以事件“-1≤log≤1”發(fā)生的概率為=,故選A.
(2)設(shè)小張和小王到校的時間分別為x和y����,則則滿足條件的區(qū)域如圖中陰影部分所示.
故所求概率P==.]
判斷幾何概型中的幾何度量形式的方法
1.當題干涉及兩個變量問題時���,一般與面積有關(guān).
2.當題干涉及一個變量問題時,要看變量可以等可能到達的區(qū)域:若變量在線段上移動��,則幾何度量是長度�;若變量在平面區(qū)域(空間區(qū)域)內(nèi)移動,則幾何度量是面積(體積).
提醒:數(shù)形結(jié)合是解決幾何概型問題的常用方法����,求解時,畫圖務(wù)必準確���、直
12�����、觀.
變式訓練2] 如圖6-1,圓C內(nèi)切于扇形AOB�,∠AOB=,若向扇形AOB內(nèi)隨機投擲600個點���,則落入圓內(nèi)的點的個數(shù)估計值為( )
圖6-1
A.100 B.200
C.400 D.450
C 如圖�,設(shè)OA與圓C相切于點D�,連接OC,CD���,∠AOB=��,則∠COD=�����,
設(shè)圓C的半徑為1�,可得OC=2��,所以扇形的半徑為3�,
由幾何概型可得點在圓C內(nèi)的概率為P===,故向扇形AOB內(nèi)隨機投擲600個點�����,則落入圓內(nèi)的點的個數(shù)估計為×600=400個.]
熱點題型3 互斥事件與對立事件的概率
題型分析:互斥事件與對立事件的概率常與古典概型等交匯命題���,主要考
13���、查學生的分析轉(zhuǎn)化能力���,難度中等.
(2016·南昌一模)現(xiàn)有甲�、乙���、丙���、丁4個學生課余參加學校社團文學社與街舞社的活動,每人參加且只能參加一個社團的活動��,且參加每個社團是等可能的.
(1)求文學社和街舞社都至少有1人參加的概率���;
(2)求甲�、乙同在一個社團����,且丙��、丁不同在一個社團的概率.
解] 甲���、乙���、丙���、丁4個學生課余參加學校社團文學社與街舞社的情況如下:
文學社
街舞社
1
甲乙丙丁
2
甲乙丙
丁
3
甲乙丁
丙
4
甲丙丁
乙
5
乙丙丁
甲
6
甲乙
丙丁
7
甲丙
乙丁
8
乙丙
甲丁
9
甲丁
乙丙
10
14���、
乙丁
甲丙
11
丙丁
甲乙
12
甲
乙丙丁
13
乙
甲丙丁
14
丙
甲乙丁
15
丁
甲乙丙
16
甲乙丙丁
共有16種情形���,即有16個基本事件.6分
(1)文學社或街舞社沒有人參加的基本事件有2個��,
故所求概率為=.9分
(2)甲�����、乙同在一個社團��,且丙�����、丁不同在一個社團的基本事件有4個���,故所求概率為=.12分
1.直接求法:將所求事件分解為一些彼此互斥事件的和�,運用互斥事件概率的加法公式計算.
2.間接求法:先求此事件的對立事件��,再用公式P(A)=1-P()求解���,即運用逆向思維(正難則反),特別是“至多”“至少”型題目����,用間
15�����、接求法會較簡便.
提醒:應(yīng)用互斥事件概率的加法公式的前提是確定各個事件是否彼此互斥.
變式訓練3] (名師押題)根據(jù)以往統(tǒng)計資料��,某地車主購買甲種保險的概率為0.5��,購買乙種保險但不購買甲種保險的概率為0.3.
(1)求該地1位車主至少購買甲��、乙兩種保險中的1種的概率��;
(2)求該地1位車主甲、乙兩種保險都不購買的概率.
解] 記事件A為“該車主購買甲種保險”�����,事件B為“該車主購買乙種保險但不購買甲種保險”����,事件C為“該車主至少購買甲�����、乙兩種保險中的1種”,事件D為“該車主甲���、乙兩種保險都不購買”.4分
(1)由題意得P(A)=0.5,P(B)=0.3����,6分
又C=A∪B,所以P(C)=P(A∪B)=P(A)+P(B)=0.5+0.3
=0.8.8分
(2)因為D與C是對立事件����,所以P(D)=1-P(C)=1-0.8=0.2.12分
 高三數(shù)學二輪復習 第1部分 專題3 突破點6 古典概型與幾何概型 理-人教高三數(shù)學試題
高三數(shù)學二輪復習 第1部分 專題3 突破點6 古典概型與幾何概型 理-人教高三數(shù)學試題