《(統(tǒng)考版)高考數(shù)學(xué)二輪專題復(fù)習 課時作業(yè)8 空間幾何體 文(含解析)-人教版高三數(shù)學(xué)試題》由會員分享��,可在線閱讀�,更多相關(guān)《(統(tǒng)考版)高考數(shù)學(xué)二輪專題復(fù)習 課時作業(yè)8 空間幾何體 文(含解析)-人教版高三數(shù)學(xué)試題(8頁珍藏版)》請在裝配圖網(wǎng)上搜索。
1���、課時作業(yè)8 空間幾何體
[A·基礎(chǔ)達標]
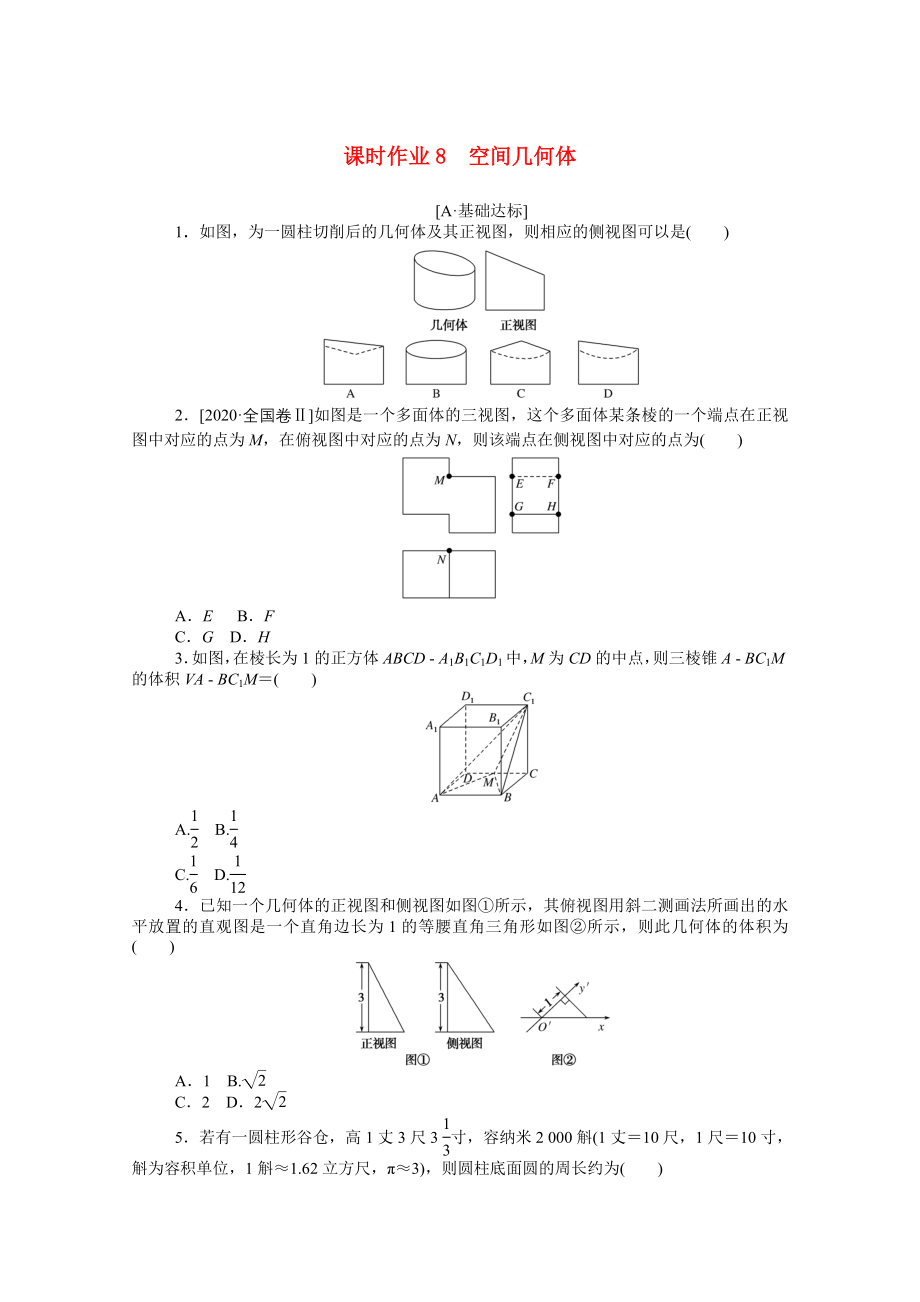
1.如圖���,為一圓柱切削后的幾何體及其正視圖��,則相應(yīng)的側(cè)視圖可以是( )
2.[2020·全國卷Ⅱ]如圖是一個多面體的三視圖�����,這個多面體某條棱的一個端點在正視圖中對應(yīng)的點為M�����,在俯視圖中對應(yīng)的點為N����,則該端點在側(cè)視圖中對應(yīng)的點為( )
A.E B.F
C.G D.H
3.如圖�����,在棱長為1的正方體ABCD - A1B1C1D1中���,M為CD的中點�����,則三棱錐A - BC1M的體積VA - BC1M=( )
A. B.
C. D.
4.已知一個幾何體的正視圖和側(cè)視圖如圖①所示���,其俯視圖用斜二測畫法所畫出的水平放置的直
2�、觀圖是一個直角邊長為1的等腰直角三角形如圖②所示���,則此幾何體的體積為( )
A.1 B.
C.2 D.2
5.若有一圓柱形谷倉��,高1丈3尺3寸,容納米2 000斛(1丈=10尺���,1尺=10寸���,斛為容積單位,1斛≈1.62立方尺�����,π≈3)�,則圓柱底面圓的周長約為( )
A.1丈3尺 B.5丈4尺
C.9丈2尺 D.48尺
6.已知圓臺上、下兩底面與側(cè)面都與球O相切�����,已知圓臺的側(cè)面積為16π��,則該圓臺上、下兩底面圓的周長之和為( )
A.4π B.6π
C.8π D.10π
7.已知矩形ABCD���,AB=2BC����,把這個矩形分別以AB�����,BC所在直線為軸旋轉(zhuǎn)一周���,
3�、所成幾何體的側(cè)面積分別記為S1�����,S2�����,則S1和S2的比值等于( )
A. B.1
C.2 D.4
8.[2020·全國卷Ⅰ]已知A���,B�,C為球O的球面上的三個點,⊙O1為△ABC的外接圓.若⊙O1的面積為4π�,AB=BC=AC=OO1,則球O的表面積為( )
A.64π B.48π
C.36π D.32π
9.已知三棱錐P - ABC的四個頂點都在球O的表面上�,PA⊥平面ABC,AB⊥BC�����,且PA=8.若平面ABC截球O所得截面的面積為9π���,則球O的表面積為( )
A.10π B.25π
C.50π D.100π
10.已知三棱錐P - ABC的棱AP,
4��、AB��,AC兩兩垂直�����,且長度都為����,以頂點P為球心,2為半徑作一個球��,則球面與三棱錐的表面相交所得到的四段弧的長度之和等于( )
A.3π B.
C. D.
11.[2020·浙江卷]已知圓錐的側(cè)面積(單位:cm2)為2π,且它的側(cè)面展開圖是一個半圓����,則這個圓錐的底面半徑(單位:cm)是________.
12.[2020·貴陽市第一學(xué)期監(jiān)測考試]平面α截球O的球面所得圓的半徑為1,球心O到平面α的距離為��,則此球的表面積是________.
13.如圖�����,在正三棱柱ABC - A1B1C1中��,D為棱AA1的中點.若AA1=4�,AB=2,則四棱錐B - ACC1D的體積為_______
5��、_.
14.某幾何體的三視圖如圖所示�����,正視圖是一個上底為2����,下底為4的直角梯形,俯視圖是一個邊長為4的等邊三角形����,則該幾何體的體積為________.
[B·素養(yǎng)提升]
1.如圖����,四棱錐P - ABCD的底面ABCD為平行四邊形����,NB=2PN,則三棱錐N - ABC與四棱錐P - ABCD的體積比為( )
A.1:2 B.1:3
C.1:6 D.1:8
2.[2020·合肥第一次教學(xué)檢測]已知正方體ABCD - A1B1C1D1����,過體對角線BD1作平面α交棱AA1于點E,交棱CC1于點F�����,則
①四邊形BFD1E一定是平行四邊形��;
②多面體ABE - DCFD1
6���、與多面體D1C1F - A1B1BE的體積相等;
③四邊形BFD1E在平面AA1D1D內(nèi)的投影一定是平行四邊形����;
④平面α有可能垂直于平面BB1D1D.
其中所有正確結(jié)論的序號為( )
A.①② B.②③④
C.①④ D.①②④
3.已知三棱錐P - ABC的四個頂點在同一個球面上��,底面△ABC滿足BA=BC=�,∠ABC=�,若該三棱錐體積的最大值為3,則其外接球的體積為________.
4.[2019·全國卷Ⅱ]中國有悠久的金石文化�����,印信是金石文化的代表之一.印信的形狀多為長方體��、正方體或圓柱體�,但南北朝時期的官員獨孤信的印信形狀是“半正多面體”(圖1).半正多面體是由兩
7、種或兩種以上的正多邊形圍成的多面體.半正多面體體現(xiàn)了數(shù)學(xué)的對稱美.圖2是一個棱數(shù)為48的半正多面體��,它的所有頂點都在同一個正方體的表面上����,且此正方體的棱長為1.則該半正多面體共有__________個面,其棱長為________.
5.在矩形ABCD中����,AB=1,AD=2�����,E為線段AD的中點,如圖1����,沿BE將△ABE折起至△PBE,使BP⊥CE���,如圖2所示.
(1)求證:平面PBE⊥平面BCDE���;
(2)求點D到平面PEC的距離.
6.
如圖,三棱柱ABC - A1B1C1的各棱長均為2�,AA1⊥平面ABC,E�,F(xiàn)分別為棱A1B1,BC的中點.
8�����、(1)求證:直線BE∥平面A1FC1���;
(2)平面A1FC1與直線AB交于點M,指出點M的位置�,說明理由,并求三棱錐B - EFM的體積.
課時作業(yè)8 空間幾何體
[A·基礎(chǔ)達標]
1.解析:由題意���,根據(jù)切削后的幾何體及其正視圖����,可得相應(yīng)的側(cè)視圖的切口為橢圓,故選B.
答案:B
2.解析:根據(jù)三視圖可得直觀圖如圖所示��,圖中的點U在正視圖中對應(yīng)的點為M��,在俯視圖中對應(yīng)的點為N��,所以該端點在側(cè)視圖中對應(yīng)的點為E.故選A.
答案:A
3.解析:VA - BC1M=VC1 - ABM=S△ABM·C1C=×AB×AD×C1C=.故選C.
答案:
9���、C
4.解析:根據(jù)直觀圖可得該幾何體的俯視圖是一個直角邊長分別是2和的直角三角形�����,根據(jù)三視圖可知該幾何體是一個三棱錐��,且三棱錐的高為3��,所以體積V=××3=.故選B.
答案:B
5.解析:由題設(shè)可得����,圓柱的體積V≈2 000×1.62=3 240(立方尺),
又圓柱的高h=10+3+=(尺)���,
設(shè)圓柱底面圓的半徑為r尺�,則有3×r2=3 240�,解得r=9,
故圓柱的底面圓的周長l≈2×3×9=54(尺)���,即5丈4尺�,故選B.
答案:B
6.解析:
圓臺的軸截面如圖所示�����,圓臺的側(cè)面積S側(cè)=π(R+r)2=16π���,所以R+r=4���,所以該圓臺上、下兩底面圓的周長之和為2(R
10����、+r)π=8π.故選C.
答案:C
7.解析:設(shè)BC=a,AB=2a���,所以S1=2π·a·2a=4πa2���,S2=2π·2a·a=4πa2,S1S2=1.故選B.
答案:B
8.解析:如圖����,由題知△ABC為等邊三角形,圓O1的半徑r=2�,即O1B=2,∴BC=2=OO1�,
在Rt△OO1B中,OB2=OO+O1B2=16���,∴球O的半徑R=OB=4�,則S球O=4πR2=64π.故選A.
答案:A
9.解析:設(shè)球O的半徑為R�����,由平面ABC截球O所得截面的面積為9π�,得△ABC的外接圓的半徑為3.設(shè)該外接圓的圓心為D,因為AB⊥BC�,所以點D為AC的中點,所以DC=3.因為PA⊥平
11�����、面ABC,易證PB⊥BC���,所以PC為球O的直徑.又PA=8�,所以O(shè)D=PA=4����,所以R=OC==5,
所以球O的表面積為S=4πR2=100π.故選D.
答案:D
10.解析:如圖所示���,由題意知Rt△PAC���,Rt△PAB為等腰直角三角形,且AP=AB=AC=.
以頂點P為球心�,2為半徑作一個球,設(shè)球P與Rt△PAC的邊PC���,AC分別交于點M����,N與AB����,PB分別交于點H�,G���,
易得cos∠APN=,所以∠APN=���,AN=AP·tan=1�,所以∠NPM=��,
所以弧MN的長l=×2=.
同理l=����,
易知AH=AN=1,則l=×1=.
又易知弧GM的長是以頂點P為圓心�,2為半徑的
12、圓的周長的�,
所以l==,
所以球面與三棱錐的表面相交所得到的四段弧的長度之和等于+++=.故選B.
答案:B
11.解析:解法一:設(shè)該圓錐的母線長為l��,因為圓錐的側(cè)面展開圖是一個半圓����,其面積為2π�,所以πl(wèi)2=2π���,解得l=2�����,所以該半圓的弧長為2π.設(shè)該圓錐的底面半徑為R�,則2πR=2π����,解得R=1.
解法二:設(shè)該圓錐的底面半徑為R,則該圓錐側(cè)面展開圖中的圓弧的弧長為2πR.因為側(cè)面展開圖是一個半圓�����,設(shè)該半圓的半徑為r����,則πr=2πR,即r=2R����,所以側(cè)面展開圖的面積為·2R·2πR=2πR2=2π,解得R=1.
答案:1
12.解析:因為平面α截球O的球面所得圓的半徑為1�����,
13、球心到該平面的距離d=����,所以球的半徑R==,根據(jù)球的表面積計算公式���,得球的表面積S=4πR2=12π.
答案:12π
13.解析:取AC的中點O,連接BO(圖略)���,則BO⊥AC���,
所以BO⊥平面ACC1D.
因為AB=2,所以BO=.
因為D為棱AA1的中點�,AA1=4,所以AD=2�����,
所以S梯形ACC1D=×(2+4)×2=6����,
所以四棱錐B - ACC1D的體積為×6×=2.
答案:2
14.解析:把三視圖還原成幾何體ABC - DEF��,如圖所示��,在AD上取點G���,使得AG=2,連接GE����,GF,則把幾何體ABC - DEF分割成三棱柱ABC - GEF和三棱錐D - GEF
14�����、����,所以VABC - DEF=VABC - GEF+VD - GEF=4×2+×4×2=.
答案:
[B·素養(yǎng)提升]
1.解析:設(shè)點P,N在平面ABCD內(nèi)的投影分別為點P′�����,N′�����,(圖略)則PP′⊥平面ABCD,NN′⊥平面ABCD���,所以PP′∥NN′�,則在△BPP′中���,由BN=2PN得=�,又因為四邊形ABCD為平行四邊形�,所以=,則==×=.
答案:B
2.解析:對于①����,由平面BCC1B1∥平面ADD1A1�����,并且B����,E,F(xiàn)��,D1四點共面��,知ED1∥BF,同理FD1∥EB��,故四邊形BFD1E一定是平行四邊形���,故①正確�;對于②��,多面體ABE - DCFD1與多面體D1C1F - A1
15�����、B1BE完全一樣��,很顯然體積相等�����,故②正確����;對于③,當投射線平行于平面BFD1E時�,投影是線段D1E,故③錯誤;對于④�����,當E和F分別是對應(yīng)棱的中點時�,平面BFD1E⊥平面BB1D1D,故④正確.故選D.
答案:D
3.解析:因為△ABC是等腰直角三角形�����,故AC為截面圓的直徑�����,故外接球的球心O在截面ABC上的投影為AC的中點D���,如圖,連接PD����,OC,當P���,O�����,D共線且P����,O位于截面ABC同一側(cè)時,該三棱錐的體積最大���,此時PD⊥平面ABC����,由××××PD=3����,解得PD=3.
設(shè)外接球的半徑為R,則OD=3-R�,OC=R,
在△ODC中�����,CD=AC=���,
由勾股定理得(3-R)2+()2
16��、=R2���,解得R=2.
所以外接球的體積V=π×23=π.
答案:π
4.解析:依題意知�,題中的半正多面體的上�����、下�、左、右�、前、后6個面都在正方體的表面上��,且該半正多面體的表面由18個正方形����,8個正三角形組成,因此題中的半正多面體共有26個面.注意到該半正多面體的俯視圖的輪廓是一個正八邊形��,設(shè)題中的半正多面體的棱長為x���,則x+x+x=1,解得x=-1����,故題中的半正多面體的棱長為-1.
答案:26?。?
5.解析:(1)證明:在題圖1中連接EC��,(圖略)由題意得∠AEB=∠CED=45°���,∠BEC=90°�����,BE⊥CE.
在題圖2中�,∵PB⊥CE�,PB∩BE=B,∴CE⊥平面PBE��,
17����、∵CE?平面BCDE,∴平面PBE⊥平面BCDE.
(2)在題圖2中���,取BE的中點O����,連接PO,(圖略)
∵PB=PE�����,∴PO⊥BE�,PO=BE=,
∵平面PBE⊥平面BCDE�����,
∴PO⊥平面BCDE����,
∴VP - ECD=S△ECD·PO=××=.
設(shè)點D到平面PEC的距離為h,
由(1)CE⊥平面PBE知CE⊥PE��,
S△PEC=PE·CE=×1×=���,
∵VD - PEC=VP - ECD���,∴h·S△PEC=h=,h=��,
∴點D到平面PEC的距離為.
6.解析:(1)證明:取A1C1的中點G�,連接EG,F(xiàn)G��,
于是EG綊B1C1�,又BF綊B1C1,
∴BF綊EG.
18����、
∴四邊形BFGE是平行四邊形.
∴BE∥FG.
而BE?平面A1FC1,F(xiàn)G?平面A1FC1���,
∴直線BE∥平面A1FC1.
(2)解:M為棱AB的中點.
理由如下:
取AB中點為M�,連接ME�,MF,F(xiàn)E��,
∵AC∥A1C1�,AC?平面A1FC1,A1C1?平面A1FC1�����,
∴直線AC∥平面A1FC1���,
又平面A1FC1∩平面ABC=FM����,
∴AC∥FM,又F為棱BC的中點���,
∴M為棱AB的中點.
∴S△BFM=S△ABC=×=�����,
∵BB1⊥平面ABC����,∴B1B為B1到平面ABC的距離.
∴VB - EFM=VE - BFM=S△BFM·BB1=××2=.
 (統(tǒng)考版)高考數(shù)學(xué)二輪專題復(fù)習 課時作業(yè)8 空間幾何體 文(含解析)-人教版高三數(shù)學(xué)試題
(統(tǒng)考版)高考數(shù)學(xué)二輪專題復(fù)習 課時作業(yè)8 空間幾何體 文(含解析)-人教版高三數(shù)學(xué)試題