《繼任市骨干教師 賓縣第四中學(xué) 初中數(shù)學(xué) 杜照輝雙解題》由會(huì)員分享,可在線閱讀�,更多相關(guān)《繼任市骨干教師 賓縣第四中學(xué) 初中數(shù)學(xué) 杜照輝雙解題(2頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。
1��、
2011 年繼任市骨干教師 賓縣第四中學(xué) 初中數(shù)學(xué) 杜照輝雙解題
已知∠ MAN=30��,點(diǎn) B 在邊 AM上���,AB=2����,點(diǎn) P 在邊 AN上��,且 BP=根號(hào) 2�,則∠ PBA 等于多少度?(答案: 105或 15)
正弦定理:
PB / sin30 =AB / sin ∠APB
所以�, sin ∠APB= (根號(hào) 2) / 2
所以, ∠ APB=45 或 135
所以���, ∠ PBA=180 -30 -∠APB=105 或 15
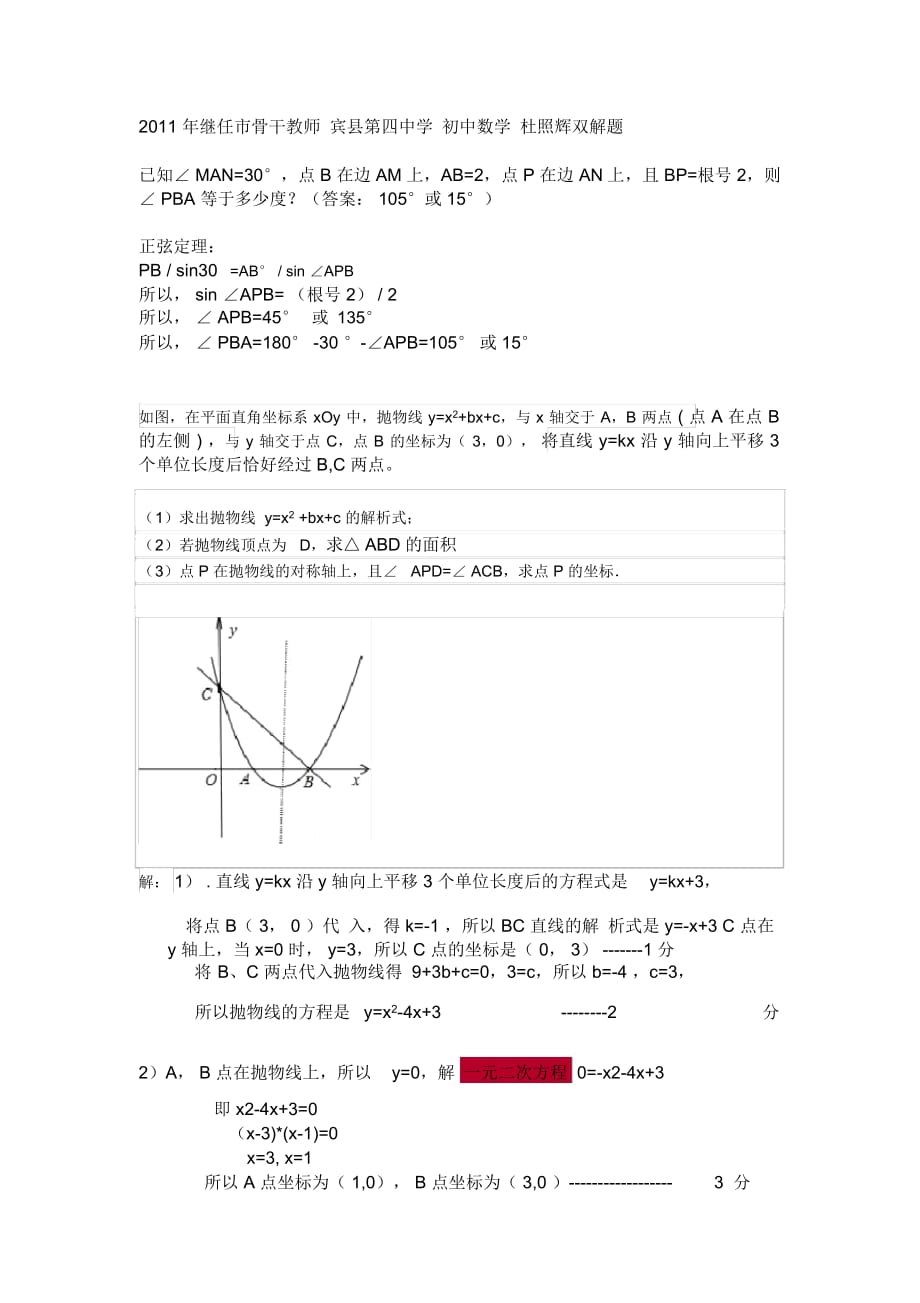
如圖����,在平面直角坐標(biāo)系 xOy 中���,拋物線 y=x2+bx+c�,與 x 軸交于 A,
2���、B 兩點(diǎn) ( 點(diǎn) A 在點(diǎn) B 的左側(cè) ) ����,與 y 軸交于點(diǎn) C��,點(diǎn) B 的坐標(biāo)為( 3��,0)�, 將直線 y=kx 沿 y 軸向上平移 3 個(gè)單位長(zhǎng)度后恰好經(jīng)過(guò) B,C 兩點(diǎn)�。
( 1)求出拋物線 y=x2 +bx+c 的解析式;
( 2)若拋物線頂點(diǎn)為 D�,求△ ABD的面積
( 3)點(diǎn) P 在拋物線的對(duì)稱軸上,且∠ APD=∠ ACB���,求點(diǎn) P 的坐標(biāo).
解: 1) . 直線 y=kx 沿 y 軸向上平移 3 個(gè)單位長(zhǎng)度后的方程式是
3���、 y=kx+3,
將點(diǎn) B( 3�, 0 )代 入���,得 k=-1 ,所以 BC 直線的解 析式是 y=-x+3 C 點(diǎn)在 y 軸上���,當(dāng) x=0 時(shí)���, y=3,所以 C 點(diǎn)的坐標(biāo)是( 0�, 3) -------1 分
將 B、C 兩點(diǎn)代入拋物線得 9+3b+c=0���,3=c����,所以 b=-4 ���,c=3�,
所以拋物線的方程是 y=x2-4x+3 --------2 分
2)A��, B 點(diǎn)在拋物線上�,所以
y=0,解 一元二次方程 0=-x2-4x+3
即 x2-4x+3=0
(x-3)*(x-1)=0
x=3, x=1
所以 A
4����、 點(diǎn)坐標(biāo)為( 1,0)���, B 點(diǎn)坐標(biāo)為( 3,0 )------------------
3 分
|AB|=4
頂點(diǎn)坐標(biāo)為 (-b/2a,(4ac-b2 )/4a)
即頂點(diǎn)坐標(biāo)為( 2,-1 )---------------
4
分
所以 △ABD 的高為 1
所以 S△ABD =1/2*4*1=2------------------
5
分
( 3)由 y=x2 -4x+3 ,
得 D(2��,-1 )��, A( 1�, 0), ∴ OB=3�, OC=3, OA=1��,AB=2����,
可得△ OBC是等腰直角三角
5�、形,
∴∠ OBC=45����, .
如圖,設(shè)拋物線對(duì)稱軸與 x 軸交于點(diǎn) F�,
∴ AF= AB=1.
過(guò)點(diǎn) A 作 AE⊥BC于點(diǎn) E.
∴∠ AEB=90度.
可得
����,
.
在△ AEC與△ AFP中�,∠ AEC=∠AFP=90,∠ ACE=∠APF���,
∴△ AEC∽△ AFP.
-------------
6
分
∴
��,
解得 PF=2.
----------------7
分
或者直接證明△ AFP∽△ DBC得出 PF=2
或者直接證明△ ABC∽△ ADP得出 PD=3��,
再得 PF=2.
∵點(diǎn) P 在拋物線的對(duì)稱軸上�����,
∴點(diǎn) P 的坐標(biāo)為( 2�, 2)或( 2��,-2 ).
------------8
分
 繼任市骨干教師 賓縣第四中學(xué) 初中數(shù)學(xué) 杜照輝雙解題
繼任市骨干教師 賓縣第四中學(xué) 初中數(shù)學(xué) 杜照輝雙解題