《2018年高中數(shù)學 第三章 導數(shù)應用 3.1.1 導數(shù)與函數(shù)的單調(diào)性課件6 北師大版選修2-2.ppt》由會員分享���,可在線閱讀�,更多相關《2018年高中數(shù)學 第三章 導數(shù)應用 3.1.1 導數(shù)與函數(shù)的單調(diào)性課件6 北師大版選修2-2.ppt(14頁珍藏版)》請在裝配圖網(wǎng)上搜索�。
1、利用導數(shù)研究函數(shù)單調(diào)性,1 �����、函數(shù) f(x) 在點 x0 處的導數(shù)定義,2 ���、某點處導數(shù)的幾何意義,3 �����、導函數(shù)的定義,函數(shù) y = f(x) 在點 x0 處的導數(shù) f (x0) 就是曲線 y = f(x) 在點 M(x0, y0) 處的切線的斜率.,一����、復習回顧:導數(shù)的相關概念,引例 已知函數(shù)y=x24x3,求證:這個函數(shù)在區(qū) 間(2�����,+)上是單調(diào)遞增的.,(1)任取x1
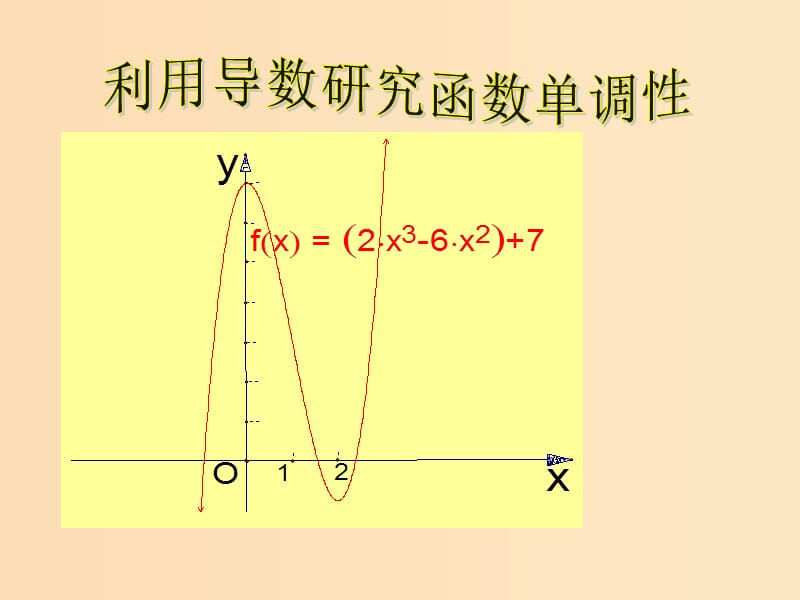
2、加量與函數(shù)值的增加量之間的關系���,于是我們設想一下能否利用導數(shù)來研究單調(diào)性呢�����?,這表明:導數(shù)的正�、負與函數(shù)的單調(diào)性密 切相關,,2,.,.,.,.,.,.,.,,,,,,,,再觀察函數(shù)y=x24x3的圖象:,曲線y=f(x)的切線的斜率就是函數(shù)y=f(x)的導數(shù).從函數(shù) 的圖像可以看到:,函數(shù)的導數(shù)與函數(shù)的單調(diào)性的關系,增函數(shù),減函數(shù),正,負,0,0,總結:該函數(shù)在區(qū)間(����,2)上單減,切線斜率小于0,即其導數(shù)為負,在區(qū)間(2,+)上單增,切線斜率大于0,即其導數(shù)為正.而當x=2時其切線斜率為0,即導數(shù)為0.函數(shù)在該點單調(diào)性發(fā)生改變.,設函數(shù)y=f(x)在某個區(qū)間內(nèi)有導數(shù)��,如果在這個區(qū)間內(nèi)y
3�����、 0���,那么y=f(x)為這個區(qū)間內(nèi)的增函數(shù);如果在這個區(qū)間內(nèi)y <0���,那么y=f(x)為這個區(qū)間內(nèi)的減函數(shù).,判斷函數(shù)單調(diào)性的常用方法: (1)定義法 (2)圖像法 (3)導數(shù)法,結論:,y 0,增函數(shù),y <0,減函數(shù),,判斷函數(shù)單調(diào)性,,,1) 如果恒有 f(x)0����,那么 y=f(x) 在這個區(qū)間(a,b)內(nèi)單調(diào)遞增;,2) 如果恒有 f(x)<0����,那么 y=f(x)在這個區(qū)間(a,b)內(nèi)單調(diào)遞減。,一般地�����,函數(shù)yf(x)在某個區(qū)間(a,b)內(nèi):,注意:如果在某個區(qū)間內(nèi)恒有f(x)=0,則f(x)為常數(shù)函數(shù).,例1����、已知導函數(shù) 的下列信息:,當10; 當x4,或x<1時, <
4����、0; 當x=4,或x=1時, =0. 試畫出函數(shù)f(x)圖象的大致形狀����。,,,臨界點,,例2、確定函數(shù)f(x)=x22x+4在哪個區(qū)間內(nèi)是增函數(shù)����,哪個區(qū)間內(nèi)是減函數(shù).,解:f(x)=(x22x+4)=2x2.,令2x20��,解得x1. 當x(1����,+)時����, f(x)0,f(x)是增函數(shù).,令2x20�����,解得x1. 當x(�,1)時,f(x)0��,f(x)是減函數(shù),你們寫對了嗎����?,利用導數(shù)討論函數(shù)單調(diào)的步驟:,(2)求導數(shù),(3)求解不等式f (x)0,求得其解集再根據(jù)解集寫出單調(diào)遞增區(qū)間 求解不等式f (x)<0�����,求得其解集再根據(jù)解集寫出單調(diào)遞減區(qū)間,(1)求定義域D,說明:函數(shù)的單調(diào)區(qū)間必定是它的定
5���、義域的子區(qū)間,故求函數(shù)的單調(diào)區(qū)間一定首先要確定函數(shù)的定義域,在求出使導數(shù)的值為正或負的x的范圍時,要與定義域求兩者的交集 單調(diào)區(qū)間不以“并集”出現(xiàn),1���、函數(shù)f(x)=x3-3x+1的減區(qū)間為( ) (A) (-1,1) (B) (1,2) (C) (-,-1) (D) (-,-1) ,(1, +),課堂練習,答案:選A,2��、判斷下列函數(shù)的單調(diào)性, 并求出單調(diào)區(qū)間:,解:,(1) 因為 , 所以,因此, 函數(shù) 在 上單調(diào)遞增.,(2) 因為 , 所以,當 , 即 時, 函數(shù) 單調(diào)遞增;,當 , 即 時, 函數(shù) 單調(diào)遞減.,1.在某個區(qū)間(a,b)內(nèi), 如果導函數(shù)大于零,那么原函數(shù)在這個區(qū)間內(nèi)單調(diào)遞增; 如果導函數(shù)小于零,那么原函數(shù)在這個區(qū)間內(nèi)單調(diào)遞減.,2.求可導函數(shù)f(x)單調(diào)區(qū)間的步驟: (1)先求定義域����,然后f(x) (2)解不等式f(x)0(或f(x)<0) (3)確認并指出遞增區(qū)間(或遞減區(qū)間),3.證明可導函數(shù)f(x)在(a,b)內(nèi)的單調(diào)性的方法: (1)先求定義域,然后求f(x) (2)確認f(x)在(a,b)內(nèi)的符號 (3)作出結論,課堂小結,
 2018年高中數(shù)學 第三章 導數(shù)應用 3.1.1 導數(shù)與函數(shù)的單調(diào)性課件6 北師大版選修2-2.ppt
2018年高中數(shù)學 第三章 導數(shù)應用 3.1.1 導數(shù)與函數(shù)的單調(diào)性課件6 北師大版選修2-2.ppt