2021-2022學(xué)年 北師大版 七年級(jí)數(shù)學(xué)上冊(cè) 1.3 截一個(gè)幾何體 習(xí)題精練【含答案】

《2021-2022學(xué)年 北師大版 七年級(jí)數(shù)學(xué)上冊(cè) 1.3 截一個(gè)幾何體 習(xí)題精練【含答案】》由會(huì)員分享，可在線(xiàn)閱讀，更多相關(guān)《2021-2022學(xué)年 北師大版 七年級(jí)數(shù)學(xué)上冊(cè) 1.3 截一個(gè)幾何體 習(xí)題精練【含答案】（8頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

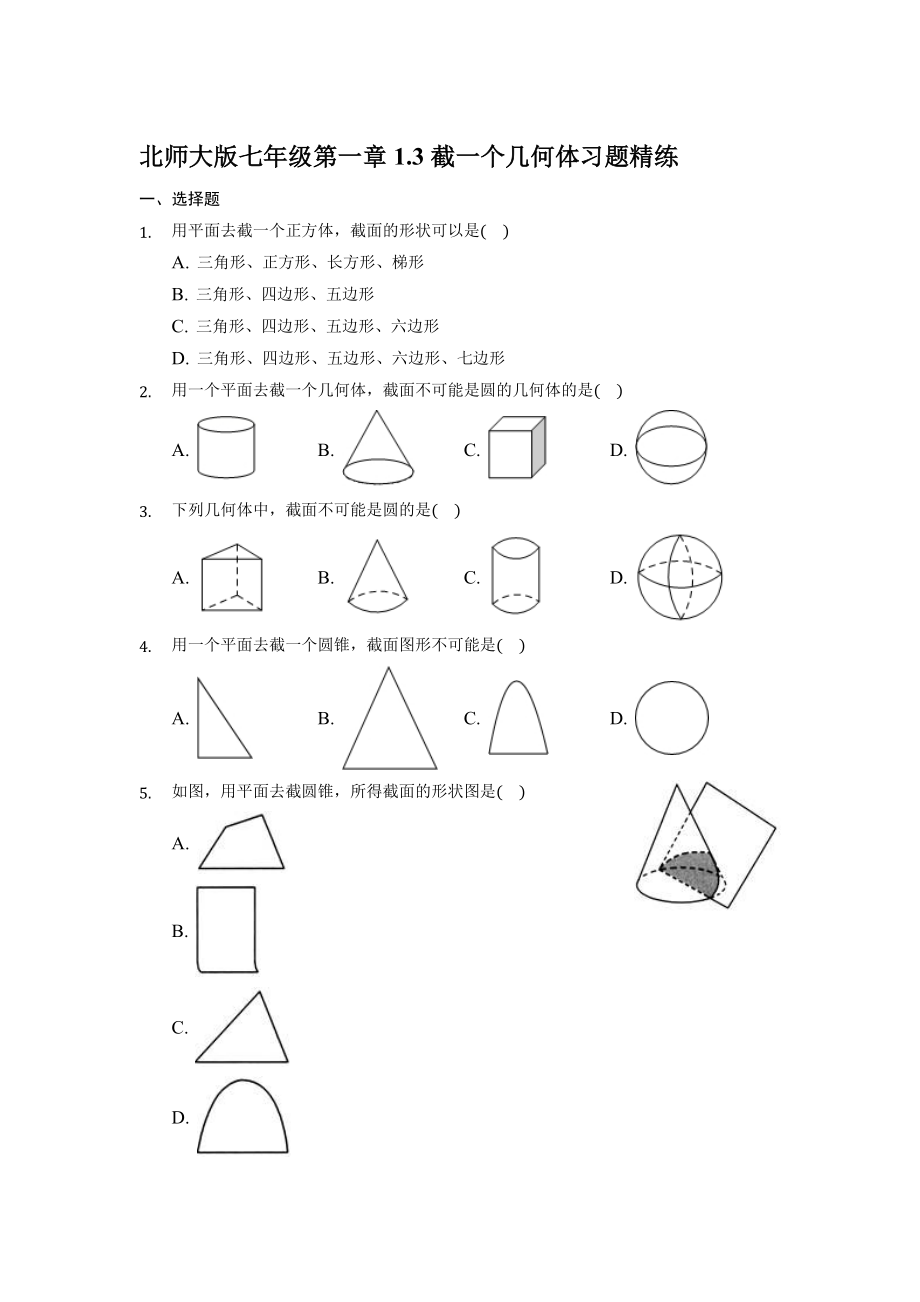
1、 北師大版七年級(jí)第一章1.3截一個(gè)幾何體習(xí)題精練 一、選擇題 1. 用平面去截一個(gè)正方體，截面的形狀可以是(????) A. 三角形、正方形、長(zhǎng)方形、梯形 B. 三角形、四邊形、五邊形 C. 三角形、四邊形、五邊形、六邊形 D. 三角形、四邊形、五邊形、六邊形、七邊形 2. 用一個(gè)平面去截一個(gè)幾何體，截面不可能是圓的幾何體的是(????) A. B. C. D. 3. 下列幾何體中，截面不可能是圓的是(????) A. B. C. D. 4. 用一個(gè)平面去截一個(gè)圓錐，截面圖形不可能是(????) A. B. C. D. 5. 如圖，用平面去截

2、圓錐，所得截面的形狀圖是(????) A. B. C. D. 6. 如圖所示，用一個(gè)平面去截一個(gè)圓柱體，截面不可能是(????)． A. B. C. D. 7. 用一個(gè)平面去截一個(gè)幾何體，下列幾何體中截面可能是圓的是(????) A. 正方體 B. 長(zhǎng)方體 C. 球 D. 六棱柱 8. 用一個(gè)平面去截下面的幾何體，所得截面是三角形，則這個(gè)幾何體不可能為(? ? )． A. B. C. D. 二、填空題 9. 在如圖所示的四個(gè)圖形中，圖形________可以用平面截長(zhǎng)方體得到；圖形________可以用平面截圓錐得到．(填序號(hào))

3、10. 用平面截一個(gè)幾何體，若截面是圓，則幾何體是______(寫(xiě)出兩種) 11. 用一個(gè)平面去截一個(gè)三棱柱，寫(xiě)出你認(rèn)為所有可能的截面形狀______． 12. 如圖，在棱長(zhǎng)分別為2cm、3cm、4cm的長(zhǎng)方體中截掉一個(gè)棱長(zhǎng)為1cm的正方體，則剩余幾何體的表面積為_(kāi)_____ ． 三、解答題 13. 如圖是用刀切去正方體的一個(gè)角得到的截面是等邊三角形的方法．請(qǐng)你實(shí)踐并思考：將正方體用刀切去一塊，它的截面可能是下列哪些圖形？不可能是哪些圖形？ 14. 根據(jù)下列描述，分別判斷該立體圖形的名稱(chēng)： (1)一個(gè)立體圖形是錐體，它的底面是六邊形；

4、(2)一個(gè)立體圖形，無(wú)論怎樣截，得到的截面都是圓． 15. 如圖，觀察下列幾何體，用平面分別截這些幾何體，請(qǐng)?jiān)诒碇刑顚?xiě)各圖形截面(陰影部分)的形狀． 圖形編號(hào) ① ② ③ ④ 截面形狀 圖形編號(hào) ⑤ ⑥ ⑦ ⑧ 截面形狀 16. 如圖，有一個(gè)立方體，它的表面涂滿(mǎn)了紅色，在它每個(gè)面上切兩刀，得到27個(gè)小立方體，而且凡是切面都是白色.問(wèn)： (1)小立方體中三面紅的有幾塊？?jī)擅婕t的呢？一面紅的呢？沒(méi)有紅色的面呢？ (2)如果每面切三刀，情況又怎樣呢？ (3)每面切n刀呢？

5、 答案和解析 1.C 解：用一個(gè)平面去截一正方體，截面可能為三角形、四邊形(梯形，矩形，正方形)、五邊形、六邊形， 只有C選項(xiàng)比較全面，符合題意． 故選：C． 2.C 解：用一個(gè)平面去截圓錐或圓柱，截面可能是圓，用一個(gè)平面去截球，截面是圓，但用一個(gè)平面去截棱柱，截面不可能是圓． 故選：C． 3.A 用一個(gè)平面去截球，截面是圓，用一個(gè)平面去截圓錐或圓柱，截面可能是圓，但用一個(gè)平面去截棱柱，截面不可能是圓． 故選A．?? 4.A 解：A、用一個(gè)平面不可能截到；符合題意， B、用一個(gè)平面沿圓錐的高線(xiàn)截取即可得到等腰三角形，故不符合題意；

6、 C、從側(cè)面截到底面得到如圖圖形，故不符合題意； D、將圓錐沿平行于底面截開(kāi)即可得到圓，故不符合題意， 故選：A． 5.D 解：根據(jù)圓錐的特點(diǎn)可知，用平面去截圓錐，平面與圓錐的側(cè)面截得一條弧線(xiàn)，與底面截得一條線(xiàn)段，所以截面的形狀應(yīng)該是D． 故選D．?? 6.B 當(dāng)截面與軸截面垂直時(shí)，得到的截面形狀是圓； 截面的形狀不可能是等腰梯形 當(dāng)截面與軸截面斜交時(shí)，得到的截面的形狀是橢圓； 當(dāng)截面與軸截面平行時(shí)，得到的形狀為長(zhǎng)方形． 故選B ．?? 7.C 解：用一個(gè)平面去截球，截面是圓，用一個(gè)平面去截正方體，長(zhǎng)方體，六棱柱都不可能是圓． 故選C． 8.B 解：A.用平面

7、截正方體，截面可能是三角形，故本選項(xiàng)錯(cuò)誤； B.用平面截圓柱，截面不是三角形，故本選項(xiàng)正確； C.用平面三棱柱，截面可能是三角形，故本選項(xiàng)錯(cuò)誤； D.用平面截圓錐，截面可能是三角形，故本選項(xiàng)錯(cuò)誤． 故選B．?? 9.②③④；①④ 解：長(zhǎng)方體可以用平面截出長(zhǎng)方形、梯形、等腰三角形等，不可能截出圓；圓錐可以截出等腰三角形和圓，不可能截出四邊形； 圖形②③④可以用平面截長(zhǎng)方體得到；圖形①④可以用平面截圓錐得到， 故答案為②③④；①④．?? 10.球或圓柱(答案不唯一) 解：用平面去截一個(gè)幾何體，若截面是圓，則幾何體是球或圓柱． 故球或圓柱(答案不唯一)． 用一個(gè)平面截一個(gè)幾何

8、體得到的面叫做幾何體的截面． 考查了截一個(gè)幾何體，截面是圓，那么該幾何體的某個(gè)視圖中應(yīng)有圓． 11.三角形、四邊形、五邊形 解：用一個(gè)平面去截一個(gè)三棱柱，截面的形狀可能為：三角形、四邊形、五邊形， 故三角形、四邊形、五邊形． 12.52cm2 解：(2×3+2×4+3×4)×2 =(6+8+12)×2 =26×2 =52(cm2). 答：剩余幾何體的表面積為52cm2． 故52cm2． 13.解：可能是①②③⑤⑥⑦⑧，不可能是④ 14.解：(1)六棱錐． (2)球． 15.解：由圖知：各圖形截面(陰影部分)的形狀為：①圓；②三角形(等腰三角形)；③圓；④長(zhǎng)

9、方形；⑤三角形；⑥梯形；⑦三角形；⑧長(zhǎng)方形． 如表： 16.解：(1)小立方體中三面紅的有8塊，兩面紅的12塊，一面紅的6塊，沒(méi)有紅色的1塊． (2)如果每面切三刀，小立方體中三面紅的有8塊，兩面紅的24塊，一面紅的24塊，沒(méi)有紅色的8塊． (3)每面切n刀，小立方體中三面紅的有8塊，兩面紅的6(2n?2)塊，一面紅的6(n?1)2塊，沒(méi)有紅色的(n?1)3塊． (1)三面紅色對(duì)應(yīng)8個(gè)頂角上的小立方塊，8個(gè)；兩面紅色對(duì)應(yīng)6條邊每條中間的那2小立方塊，12個(gè)；一面紅色對(duì)應(yīng)6個(gè)面每個(gè)面中心的那個(gè)小立方塊，6個(gè)；最后各面都沒(méi)有顏色對(duì)應(yīng)大立方體中心的那個(gè)小立方塊，1個(gè)；進(jìn)行計(jì)算即可；

10、(2)每面切三刀，可得64個(gè)小立方體，三面紅色對(duì)應(yīng)8個(gè)頂角上的小立方塊，8個(gè)；兩面紅色對(duì)應(yīng)6條邊每條中間的那4小立方塊，24個(gè)；一面紅色對(duì)應(yīng)6個(gè)面每個(gè)面中心的那4小立方塊，24個(gè)；最后各面都沒(méi)有顏色對(duì)應(yīng)大立方體中心的那個(gè)小立方塊，23=8個(gè)； (3)每面切n刀，可得(n+1)3個(gè)小立方體，三面紅色對(duì)應(yīng)8個(gè)頂角上的小立方塊，8個(gè)；兩面紅色對(duì)應(yīng)6條邊每條中間的那(2n?2)小立方塊，6(2n?2)個(gè)；一面紅色對(duì)應(yīng)6個(gè)面每個(gè)面中心的那(n?1)2小立方塊，6(n?1)2個(gè)；最后各面都沒(méi)有顏色對(duì)應(yīng)大立方體中心的那個(gè)小立方塊，(n?1)3個(gè)． 本題主要考查了截一個(gè)幾何體，應(yīng)結(jié)合立體圖形的有關(guān)知識(shí)進(jìn)行分析，并根據(jù)生活實(shí)際進(jìn)行解答．