《2020屆高三數(shù)學(xué)二輪復(fù)習(xí)專題能力提升訓(xùn)練12 三視圖及空間幾何體的計(jì)算問題 理》由會員分享�����,可在線閱讀�����,更多相關(guān)《2020屆高三數(shù)學(xué)二輪復(fù)習(xí)專題能力提升訓(xùn)練12 三視圖及空間幾何體的計(jì)算問題 理(6頁珍藏版)》請?jiān)谘b配圖網(wǎng)上搜索。
1�����、訓(xùn)練12 三視圖及空間幾何體的計(jì)算問題
(時(shí)間:45分鐘 滿分:75分)
一�����、選擇題(每小題5分,共25分)
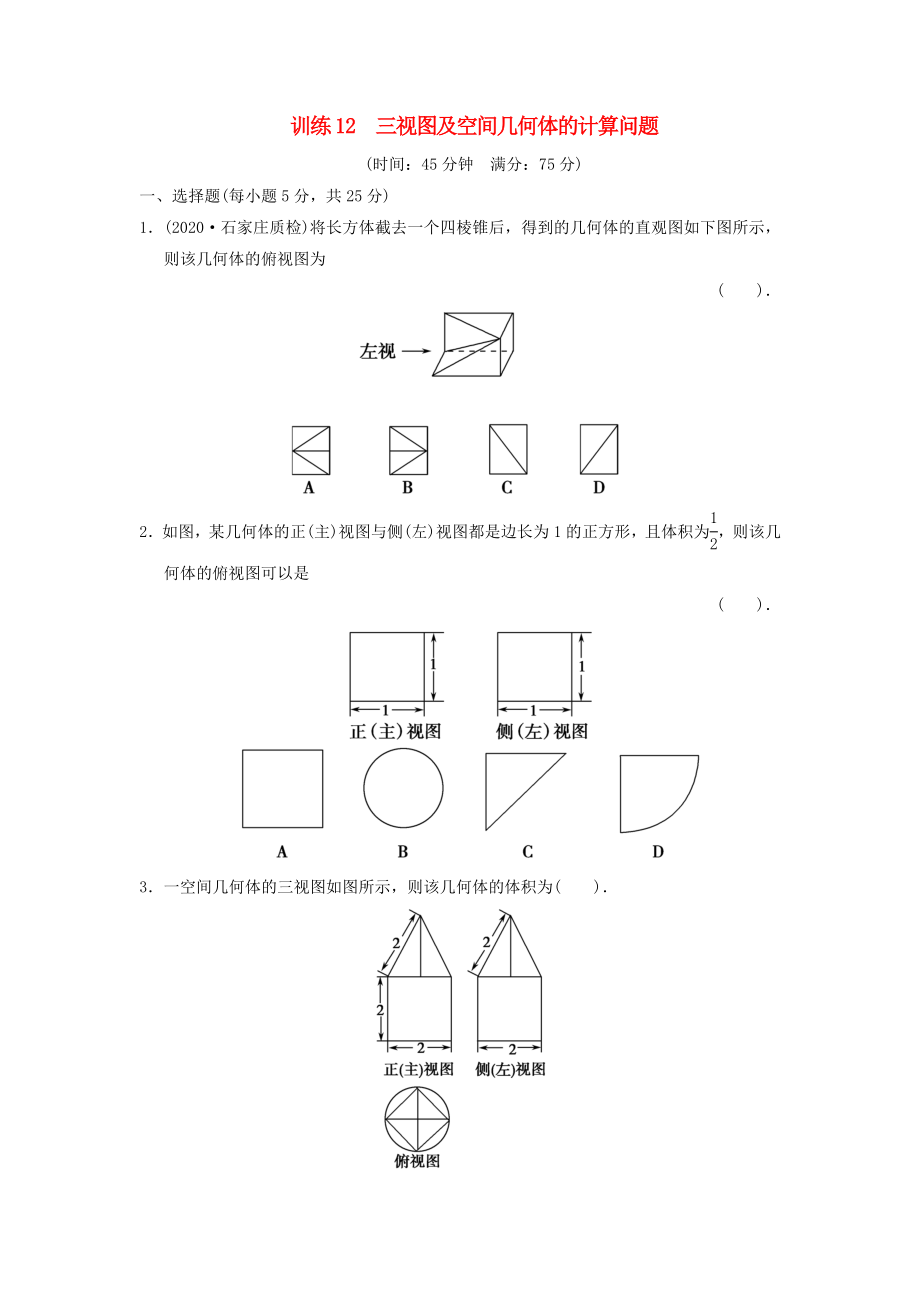
1.(2020·石家莊質(zhì)檢)將長方體截去一個(gè)四棱錐后�����,得到的幾何體的直觀圖如下圖所示,則該幾何體的俯視圖為
( ).
2.如圖�����,某幾何體的正(主)視圖與側(cè)(左)視圖都是邊長為1的正方形�����,且體積為�����,則該幾何體的俯視圖可以是
( ).
3.一空間幾何體的三視圖如圖所示,則該幾何體的體積為( ).
A.2π+2
B.4π+2
C.2π+
D.4π+
4.(2020·唐山一模)點(diǎn)A�����、B�����、C�����、D均在同一球面上,其中△ABC是正三角形�����,AD⊥平面A
2�����、BC�����,AD=2AB=6�����,則該球的體積為( ).
A.32π B.48π C.64π D.16π
5.(2020·遼寧)已知球的直徑SC=4�����,A�����,B是該球球面上的兩點(diǎn)�����,AB=�����,∠ASC=∠BSC=30°�����,則棱錐SABC的體積為( ).
A.3 B.2 C. D.1
二�����、填空題(每小題5分�����,共15分)
6.(2020·泉州模擬)一個(gè)三棱錐的正(主)視圖和側(cè)(左)視圖及其尺寸如圖所示,則該三棱錐俯視圖的面積為________.
7.(2020·青島一模)已知某棱錐的三視圖如下圖所示�����,則該棱錐的體積為________.
8.(2020·鄭州一質(zhì)測)在三棱錐ABCD
3�����、中�����,AB=CD=6,AC=BD=AD=BC=5�����,則該三棱錐的外接球的表面積為________.
三�����、解答題(本題共3小題,共35分)
9.(11分)(2020·揭陽一模)已知一四棱錐PABCD的三視圖
如右�����,求四棱錐PABCD的體積.
10.(12分)半徑為R的球有一個(gè)內(nèi)接圓柱,這個(gè)圓柱的底面
半徑為何值時(shí)�����,它的側(cè)面積最大�����?最大值是多少�����?
11.(12分)如圖�����,已知正四棱錐的底面邊長為a,側(cè)棱長為a.求:
(1)它的外接球的體積;
(2)它的內(nèi)切球的表面積.
參考答案
訓(xùn)練12 三視圖及空間幾何體的計(jì)算問題
1.C [如圖�����,當(dāng)俯視時(shí)�����,P與B�����,Q與C�����,R與D重合�����,故
4�����、選C.]
2.C [因?yàn)轶w積為,而高為1,所以底面為一個(gè)直角三角形.故選C.]
3.C [由幾何體的三視圖可知�����,該幾何體是由一個(gè)底面直徑和高都是2的圓柱和一個(gè)底面邊長為�����,側(cè)棱長為2的正四棱錐疊放而成.故該幾何體的體積為V=π×12×2+×()2×=2π+�����,故選C.]
4.A [如圖所示�����,O1為三角形ABC的外心�����,過O做OE⊥AD�����,∴OO1⊥面ABC,
∴AO1=AB=�����,∵OD=OA�����,
∴E為DA的中點(diǎn)�����,∵AD⊥面ABC,
∴AD∥OO1�����,∴EO=AO1=,
∴DO==2�����,
∴R=DO=2,
∴V=π(2)3=32π.]
5.C [如圖�����,由Rt△ASC≌Rt△BSC�����,
5、得CB=CA�����,SA=SB.
設(shè)AB的中點(diǎn)為M�����,則SM⊥AB�����,CM⊥AB,故AB⊥面SMC.
故VSABC=VASCM+VBSCM
=AB·S△SCM.
在Rt△SAC與Rt△SMA中�����,
可求SA=2,
AC=2�����,SM=.
由cos∠ASC=cos∠MSC·cos∠ASM�����,
得=cos∠MSC·,可得cos∠MSC=�����,
故sin∠MSC==�����,
∴VSABC=AB·S△SCM=×××4××=�����,故選C.]
6.解析 該三棱錐俯視圖為直角三角形�����,兩直角邊分別為1,2,其面積為×1×2=1.
答案 1
7.解析 由三視圖可知該幾何體為四棱錐�����,底面為直角梯形其面積為(2+1)×2
6�����、=3�����,高為2,所以V=×3×2=2.
答案 2
8.解析 該三棱錐在一個(gè)長方體內(nèi)�����,設(shè)長方體的長�����、寬、高分別為a�����,b,c�����,則有∴
外接球的半徑為=�����,
∴S=4π×2=43π.
答案 43 π
9.解 由該四棱錐的三視圖可知�����,該四棱錐PABCD的底面是邊長為1的正方形�����,側(cè)棱PC⊥底面ABCD�����,且PC=2,所以VPABCD=S四邊形ABCD·PC=.
10.解 取圓柱的一個(gè)軸截面ABCD�����,則⊙O為球的一個(gè)大圓.設(shè)圓柱的半徑為r�����,高為h,側(cè)面積為S.
連接OB�����,作OH⊥AB交AB于H.
在Rt△OBH中�����,有2=R2-r2�����,即h=2.
所以S=2πrh=2πr·2=4πr·�����,
所
7�����、以S2=16π2r2(R2-r2)=-16π2(r2)2+16π2R2r2.
因?yàn)檫@是一個(gè)關(guān)于r2的二次函數(shù),
所以�����,當(dāng)r2=-=�����,
即r=R時(shí)�����,S有最大值,
最大值為4π·R× =2πR2.
故當(dāng)這個(gè)圓柱的底面半徑為R時(shí)�����,它的側(cè)面積最大,最大值是2πR2.
11.解 (1)設(shè)外接球的半徑為R�����,球心為O�����,則OA=OC=OS�����,所以O(shè)為△SAC的外心,即△SAC的外接圓半徑就是球的半徑.
因?yàn)锳B=BC=a�����,所以AC=a.
所以△SAC為正三角形.
由正弦定理得�����,2R===a�����,
因此R=a�����,則V外接球=πR3=πa3.
(2)設(shè)內(nèi)切球的半徑為r.
作SE⊥底面于E,作SF⊥BC于F�����,連接EF.
則有SF== =a�����,
所以S△SBC=BC·SF=a×a=a2�����,
所以S棱錐全=4S△SBC+S底=(+1)a2.
又SE== =a�����,
所以V棱錐=S底×h=a2×a=a3.
所以r===a�����,
所以S球=4πr2=πa2.
 2020屆高三數(shù)學(xué)二輪復(fù)習(xí)專題能力提升訓(xùn)練12 三視圖及空間幾何體的計(jì)算問題 理
2020屆高三數(shù)學(xué)二輪復(fù)習(xí)專題能力提升訓(xùn)練12 三視圖及空間幾何體的計(jì)算問題 理