（人教通用）2019年中考數(shù)學(xué)總復(fù)習(xí) 第四章 幾何初步知識(shí)與三角形 第14課時(shí) 三角形與全等三角形知能優(yōu)化訓(xùn)練

《（人教通用）2019年中考數(shù)學(xué)總復(fù)習(xí) 第四章 幾何初步知識(shí)與三角形 第14課時(shí) 三角形與全等三角形知能優(yōu)化訓(xùn)練》由會(huì)員分享，可在線閱讀，更多相關(guān)《（人教通用）2019年中考數(shù)學(xué)總復(fù)習(xí) 第四章 幾何初步知識(shí)與三角形 第14課時(shí) 三角形與全等三角形知能優(yōu)化訓(xùn)練（4頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

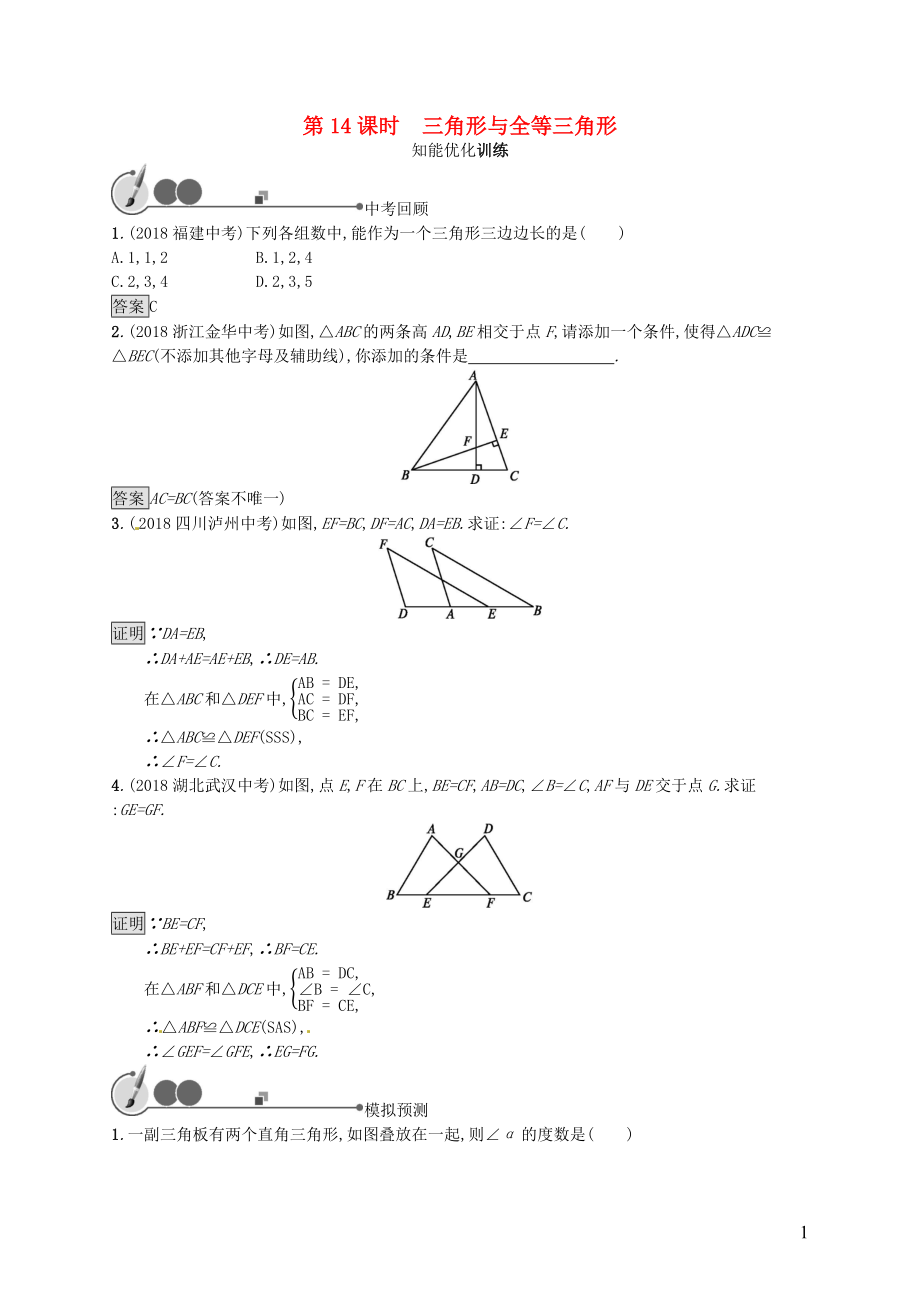
1、第14課時(shí)三角形與全等三角形知能優(yōu)化訓(xùn)練中考回顧1.(2018福建中考)下列各組數(shù)中,能作為一個(gè)三角形三邊邊長(zhǎng)的是()A.1,1,2B.1,2,4C.2,3,4D.2,3,5答案C2.(2018浙江金華中考)如圖,ABC的兩條高AD,BE相交于點(diǎn)F,請(qǐng)?zhí)砑右粋€(gè)條件,使得ADCBEC(不添加其他字母及輔助線),你添加的條件是.答案AC=BC(答案不唯一)3.(2018四川瀘州中考)如圖,EF=BC,DF=AC,DA=EB.求證:F=C.證明DA=EB,DA+AE=AE+EB,DE=AB.在ABC和DEF中,AB=DE,AC=DF,BC=EF,ABCDEF(SSS),F=C.4.(2018湖北武漢

2、中考)如圖,點(diǎn)E,F在BC上,BE=CF,AB=DC,B=C,AF與DE交于點(diǎn)G.求證:GE=GF.證明BE=CF,BE+EF=CF+EF,BF=CE.在ABF和DCE中,AB=DC,B=C,BF=CE,ABFDCE(SAS),GEF=GFE,EG=FG.模擬預(yù)測(cè)1.一副三角板有兩個(gè)直角三角形,如圖疊放在一起,則的度數(shù)是()A.165B.120C.150D.135答案A2.如圖,在ABC中,ADBC于點(diǎn)D,BEAC于點(diǎn)E,AD與BE相交于點(diǎn)F.若BF=AC,則ABC的大小是()A.40B.45C.50D.60答案B3.如圖,已知點(diǎn)A,D,B,F在一條直線上,AC=EF,AD=BF,要使ABCF

3、DE,還需添加一個(gè)條件,這個(gè)條件可以是.(只需填一個(gè)即可)答案A=F(答案不唯一)4.若a,b,c為三角形的三邊,且a,b滿足a2-9+(b-2)2=0,則第三邊c的取值范圍是.答案1c55.如圖,ACE是以ABCD的對(duì)角線AC為邊的等邊三角形,點(diǎn)C與點(diǎn)E關(guān)于x軸對(duì)稱.若點(diǎn)E的坐標(biāo)是(7,-33),則點(diǎn)D的坐標(biāo)是.答案(5,0)6.如圖,在ABC中,CD是ACB的平分線,A=80,ACB=60,則BDC=.答案1107.在邊長(zhǎng)為1的等邊三角形ABC中,中線AD與中線BE相交于點(diǎn)O,則OA長(zhǎng)度為.答案338.如圖,BAC=ABD=90,AC=BD,點(diǎn)O是AD,BC的交點(diǎn),點(diǎn)E是AB的中點(diǎn).(1)

4、圖中有哪幾對(duì)全等三角形?請(qǐng)寫出來.(2)試判斷OE和AB的位置關(guān)系,并給予證明.解(1)ABCBAD,AOEBOE,AOCBOD.(2)OEAB.證明:在RtABC和RtBAD中,AC=BD,BAC=ABD,AB=BA,ABCBAD(SAS),CBA=DAB,OA=OB.點(diǎn)E是AB的中點(diǎn),OEAB.9.(1)問題發(fā)現(xiàn):如圖甲,ACB和DCE均為等邊三角形,點(diǎn)A,D,E在同一直線上,連接BE.填空:AEB的度數(shù)為;線段AD,BE之間的數(shù)量關(guān)系是.(2)拓展探究:如圖乙,ACB和DCE均為等腰直角三角形,ACB=DCE=90,點(diǎn)A,D,E在同一直線上,CM為DCE中DE邊上的高,連接BE.請(qǐng)判斷AEB的度數(shù)及線段CM,AE,BE之間的數(shù)量關(guān)系,并說明理由.解(1)60AD=BE可證CDACEB.CEB=CDA=120.又CED=60,AEB=120-60=60.可證CDACEB,AD=BE.(2)AEB=90.AE=2CM+BE.理由:ACB和DCE均為等腰直角三角形.ACB=DCE=90.AC=BC,CD=CE,ACB-DCB=DCE-DCB,即ACD=BCE.ACDBCE,AD=BE,BEC=ADC=135,AEB=BEC-CED=135-45=90.在等腰直角三角形DCE中,CM為斜邊DE上的高.CM=DM=ME,DE=2CM.AE=DE+AD=2CM+BE.4