蘇科版八年級上冊數(shù)學(xué) 第一章全等三角形 小結(jié)與思考 教案

《蘇科版八年級上冊數(shù)學(xué) 第一章全等三角形 小結(jié)與思考 教案》由會員分享，可在線閱讀，更多相關(guān)《蘇科版八年級上冊數(shù)學(xué) 第一章全等三角形 小結(jié)與思考 教案（3頁珍藏版）》請在裝配圖網(wǎng)上搜索。

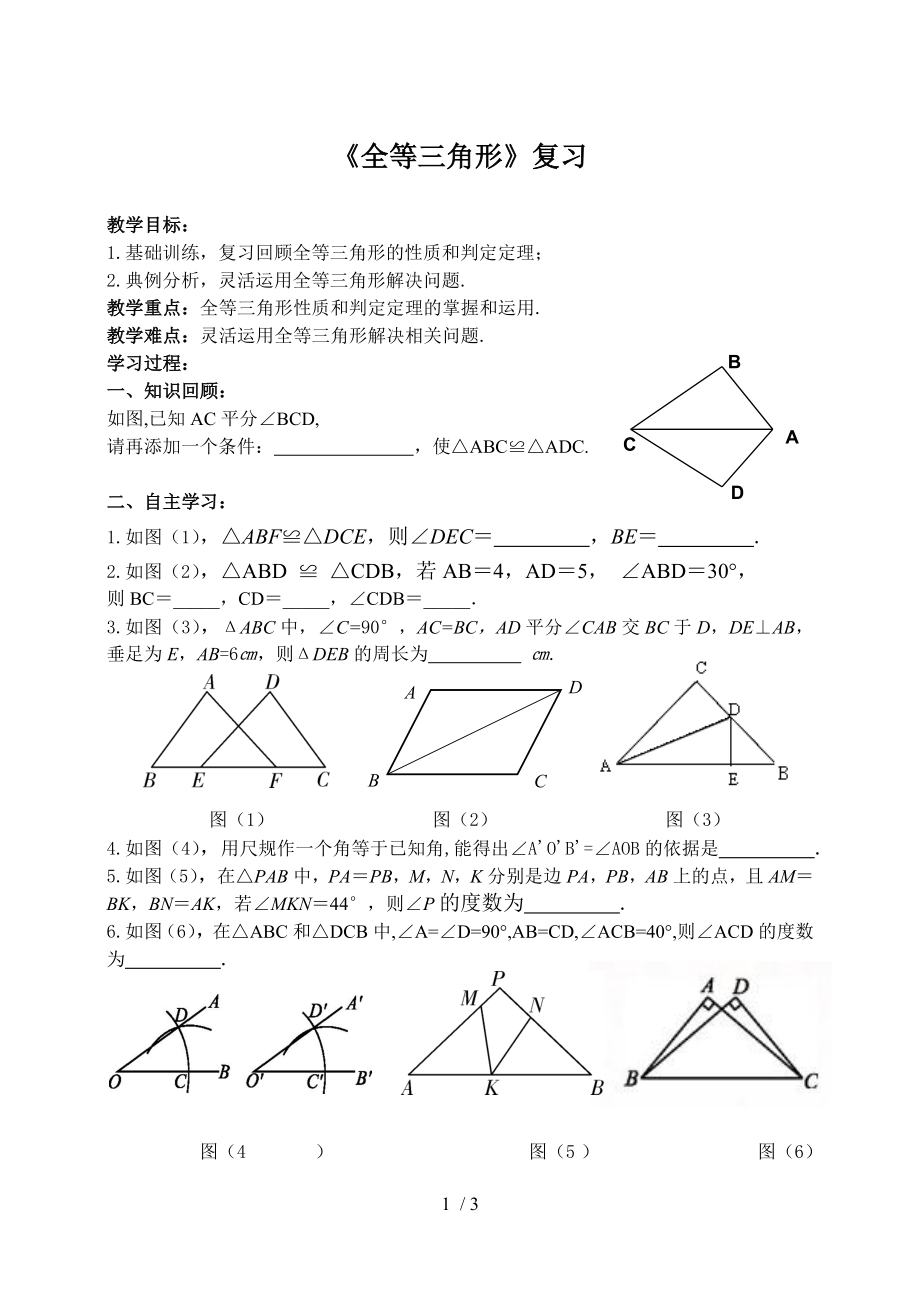
1、《全等三角形》復(fù)習(xí) 教學(xué)目標(biāo)： 1.基礎(chǔ)訓(xùn)練，復(fù)習(xí)回顧全等三角形的性質(zhì)和判定定理； 2.典例分析，靈活運用全等三角形解決問題. 教學(xué)重點：全等三角形性質(zhì)和判定定理的掌握和運用. D C A B 教學(xué)難點：靈活運用全等三角形解決相關(guān)問題. 學(xué)習(xí)過程： 一、知識回顧： 如圖,已知AC平分∠BCD, 請再添加一個條件：　 　，使△ABC≌△ADC. 二、自主學(xué)習(xí)： 1.如圖（1），△ABF≌△DCE，則∠DEC＝　 ，BE＝　 . 2.如圖（2），△ABD ≌ △CDB，若AB＝4，AD＝5， ∠ABD

2、＝30°， 則BC＝_____，CD＝_____，∠CDB＝_____． A B D C 3.如圖（3），ΔABC中，∠C=90°，AC=BC，AD平分∠CAB交BC于D，DE⊥AB，垂足為E，AB=6㎝，則ΔDEB的周長為 ㎝. 圖（1） 圖（2） 圖（3） 4.如圖（4），用尺規(guī)作一個角等于已知角,能得出∠A'O'B'=∠AOB的依據(jù)是　 . 5.如圖（5），在△PAB中，PA＝PB，M，N，K分別是邊PA，PB，AB上的點，且AM＝BK，BN＝AK，若∠

3、MKN＝44°，則∠P的度數(shù)為　 . 6.如圖（6），在△ABC和△DCB中,∠A=∠D=90°,AB=CD,∠ACB=40°,則∠ACD的度數(shù)為　 . 圖（4） 圖（5） 圖（6） 三、典例分析： 例1. 如圖，M是△ABC的邊BC的中點，AN平分∠BAC，BNAN于點N，延長BN交AC于點D，已知AB=10，BC=15，MN=3（1）求證：BN=DN（2）求△ABC的周長. 例2.如圖，在中，，點在線段上運動（D不與B、C重合），連接AD，作，交線段于．

4、（1）當(dāng)時， °, °；點D從B向C運動時，逐漸變 （填“大”或“小”）； D 40° A B C 40° E （2）當(dāng)?shù)扔诙嗌贂r，≌，請說明理由； 例3.如圖,在△ABC中,分別以AC,BC為邊作等邊三角形ACD和等邊三角形BCE.設(shè)△ACD,△BCE,△ABC的面積分別是S1,S2,S3.現(xiàn)有如下結(jié)論: （1）S1∶S2=AC2∶BC2; （2）連接AE,BD,則△BCD≌△ECA; （3）若AE、BD相交于點O,則∠AOD=60°; （4）若AC⊥BC,則S1·S2=. 其中正確結(jié)論的序號

5、是　　 　　.? 四、自主檢測： 1.如圖，已知∠B＝∠D，AB＝DE，要推得△ABC≌△DEC； （1）若以“SAS”為依據(jù)，缺條件 ； （2）若以“ASA”為依據(jù)，缺條件________________； （3）若以“AAS”為依據(jù)，缺條件_________________. 2.如圖，AB⊥CD，且AB＝CD．E，F(xiàn)是AD上兩點，CE⊥AD，BF⊥AD．若CE＝a，BF＝b，EF＝c，則AD的長為(　　) A．a(chǎn)＋c B．b＋c C．a(chǎn)－b＋c D．a(chǎn)＋b－c O A C B D 3.如圖:

6、AC和DB相交于點O,若AB=DC，AC=DB，則∠B=∠C,請說明理由. 4.在數(shù)學(xué)活動課中，小輝將邊長為和3的兩個正方形放置在直線l上，如圖 (1)，他連接AD，CF，經(jīng)測量發(fā)現(xiàn)AD＝CF. (1)他將正方形ODEF繞O點逆時針旋轉(zhuǎn)一定的角度，如圖(2)，試判斷AD與CF還相等嗎？說明你的理由； (2)他將正方形ODEF繞點O逆時針旋轉(zhuǎn)，使點E旋轉(zhuǎn)至直線l上，如圖(3)，請你求出CF的長． 圖（1） 圖（2） 圖（3） 五、自主小結(jié)： 與同學(xué)交流本節(jié)課的收獲…… 3 / 3