2022-2020學(xué)年高二數(shù)學(xué)下學(xué)期第一次月考試題 文(實(shí)驗(yàn)班)

《2022-2020學(xué)年高二數(shù)學(xué)下學(xué)期第一次月考試題 文(實(shí)驗(yàn)班)》由會員分享，可在線閱讀，更多相關(guān)《2022-2020學(xué)年高二數(shù)學(xué)下學(xué)期第一次月考試題 文(實(shí)驗(yàn)班)（10頁珍藏版）》請?jiān)谘b配圖網(wǎng)上搜索。

1、2022-2020學(xué)年高二數(shù)學(xué)下學(xué)期第一次月考試題 文(實(shí)驗(yàn)班) 注意事項(xiàng)： 1．答卷前，考生先檢查試卷與答題卷是否整潔無缺損，并用黑色字跡的簽字筆在答題卷指定位置填寫自己的班級、姓名、學(xué)號和座位號。 2．選擇題每小題選出答案后，請將答案填寫在答題卷上對應(yīng)的題目序號后，如需改動，用橡皮擦干凈后，再選涂其它答案，答案不能答在試卷上。不按要求填涂的，答案無效。 3．非選擇題必須用黑色字跡的簽字筆作答，答案必須寫在答題卷各題目指定區(qū)域內(nèi)相應(yīng)位置上，請注意每題答題空間，預(yù)先合理安排；如需改動，先劃掉原來的答案，然后再寫上新的答案；不準(zhǔn)使用鉛筆和涂改液。不按以上要求作答的答案無效。 4．考生必

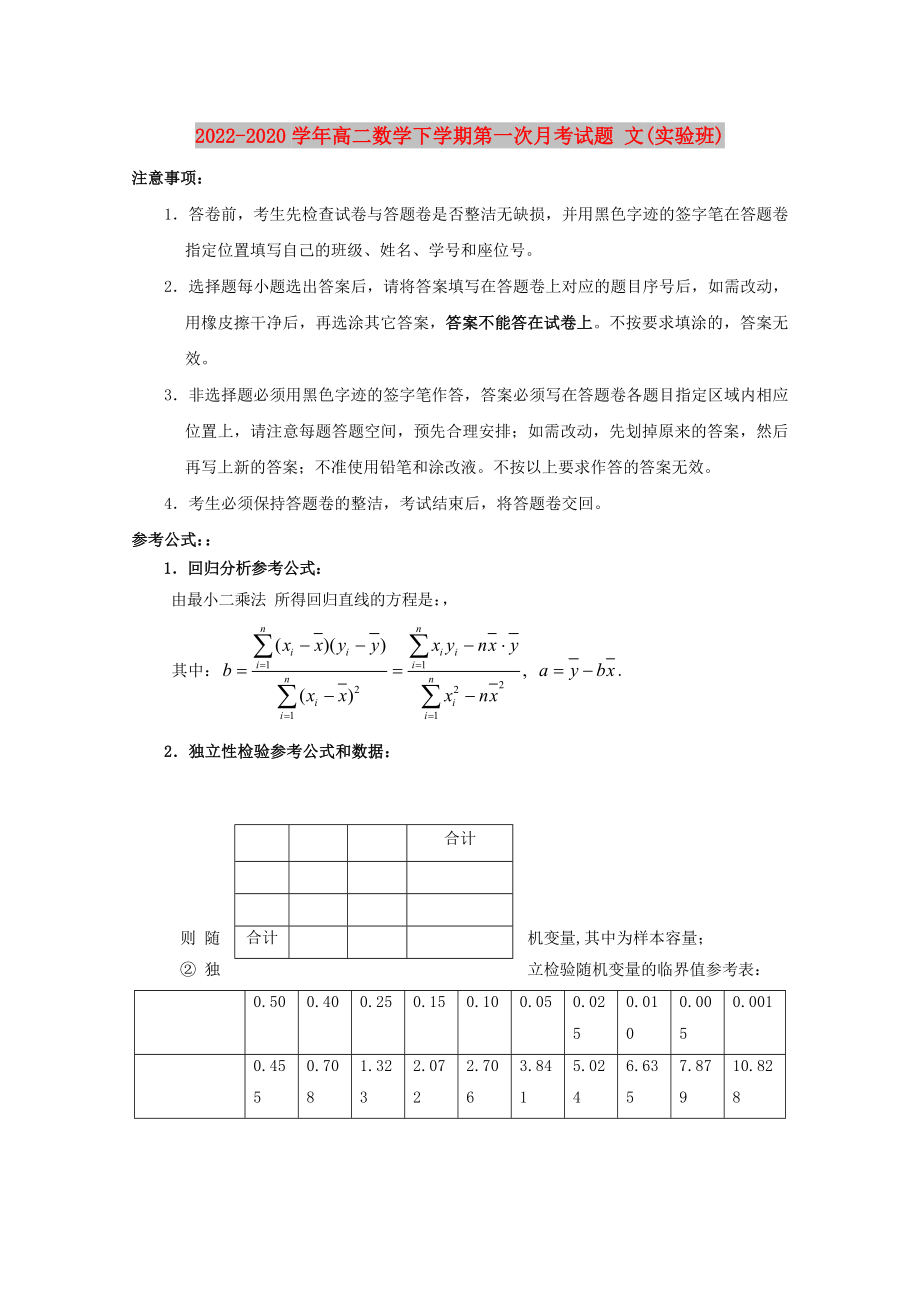
2、須保持答題卷的整潔，考試結(jié)束后，將答題卷交回。 參考公式：： 1．回歸分析參考公式： 由最小二乘法 所得回歸直線的方程是：， 其中：. 2．獨(dú)立性檢驗(yàn)參考公式和數(shù)據(jù)： 合計(jì) 合計(jì) 則隨機(jī)變量,其中為樣本容量； ②獨(dú)立檢驗(yàn)隨機(jī)變量的臨界值參考表： 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635

3、7.879 10.828 一、選擇題：本大題共12小題，每小題5分，滿分60分． 1．用演繹推理推證“正方形的對角線互相垂直”中，用到下列三個判斷：①正方形是菱形；②菱形的對角線互相垂直；③正方形的對角線互相垂直.則大前提、小前提、結(jié)論分別是　　　　　 (A) ①②③ ( B) ③②① (C) ①③② (D) ②①③ 1 1 1 2 1 1 3 3 1 1 a 6 4 1 1 5 10 10 5 1 2． 右邊所示的三角形數(shù)組是我國古代數(shù)學(xué)家楊輝發(fā)現(xiàn)的， 稱為楊輝三角形，根據(jù)圖中的數(shù)構(gòu)成的規(guī)律，所表示

4、的數(shù)是　　　　　　　　　　　　　　　　 (A) 2 ( B) 4 (C) 6 (D)8 3.命題“三角形中最多只有一個內(nèi)角是直角”的結(jié)論的否定是　　　　　　　 (A) 三角形中有兩個內(nèi)角是直角 ( B) 三角形的內(nèi)角都是直角 (C)三角形中至少有兩個內(nèi)角是直角 (D)三角形中沒有一個內(nèi)角是直角 4．用火柴棒按下圖的方法搭三角形: 按圖示的規(guī)律搭下去,則所用火柴棒數(shù) 與所搭三角形的個數(shù)之間的關(guān)系式可以是 A. ( B) (C) (D) 5

5、．已知整數(shù)對按如下規(guī)律排成一列：（1，1），（1，2），（2，1），（1，3），（2，2），（3，1）， （1，4），（2，3），（3，2），（4，1），……，則第70個數(shù)對是 ……………………………………… 圖2 (A)（10，1） ( B)（5，10） (C)（4，10） (D) （10，4） 6．如圖2所示的三角形數(shù)陣叫“萊布尼茲調(diào)和三角形”，

6、 它們是由整數(shù)的倒數(shù)組成的，第行有個數(shù)且兩端 的數(shù)均為，每個數(shù)是它下一行左右相鄰兩數(shù) 的和，如，，，…， 則第10行第4個數(shù)（從左往右數(shù)）為 (A) ( B) (C) (D) 7．已知與之間的一組數(shù)據(jù)： x 1 2 3 4 y m 3.2 4.8 7.5 若關(guān)于的線性回歸方程為，則的值為 (A) l ( B) 0.85 ( C) 0.7 (D) 0.5 8．為了調(diào)查中學(xué)生課外閱讀古典文學(xué)名著的情況，某校學(xué)生會從男生中隨機(jī)抽取了50人，從女生中隨機(jī)抽取了60人參加古典文

7、學(xué)名著知識競賽，統(tǒng)計(jì)數(shù)據(jù)如下表所示，經(jīng)計(jì)算，則測試成績是否優(yōu)秀與性別有關(guān)的把握為 優(yōu)秀 非優(yōu)秀 總計(jì) 男生 35 15 50 女生 25 35 60 總計(jì) 60 50 110 (A) 90% ( B) 95% (C) 99.5% (D) 99.9% 9．一名法官在審理一起珍寶盜竊案時，四名嫌疑人甲、乙、丙、丁的供詞如下，甲說：“罪犯在乙、丙、丁三人之中”；乙說：“我沒有作案，是丙偷的”；丙說：“甲、乙兩人中有一人是小偷”；丁說：“乙說的是事實(shí)”．經(jīng)過調(diào)查核實(shí)，四人中有兩人說的是真話，另外兩人說的是假話，且這四人中只有一人是

8、罪犯，由此可判斷罪犯是( ) (A) 甲 ( B) 乙 (C) 丙 (D) 丁 10．已知數(shù)列滿足，則= (A) 0 ( B) (C) (D) 11．如圖，圓周上按順時針方向標(biāo)有1，2，3，4，5五個點(diǎn)．一只 青蛙按順時針方向繞圓從一點(diǎn)跳到另一點(diǎn)．若它停在奇數(shù)點(diǎn)上， 則下一次只能跳一個點(diǎn)；停在偶數(shù)點(diǎn)上，則跳兩個點(diǎn)．該青蛙 從5這點(diǎn)跳起，經(jīng)xx次跳后它將停在的點(diǎn)是 (A)

9、( B) (C) (D) 12．把正奇數(shù)數(shù)列的各項(xiàng)從小到大依次排成如下三角形狀數(shù)表： 1 3 5 7 9 11 13 15 17 19 … … … … … 記表示該表中第s行的第t個數(shù)，則表中的奇數(shù)xx對應(yīng)于 (A) ( B) (C) (D) 二、填空題：本大題共4小題，每小題5分，滿分20分． 13．在數(shù)列中，，通過計(jì)算，由此猜想這個數(shù)列的通項(xiàng)公式為_______________． 14．如圖是一個有層的六邊形點(diǎn)陣.它的中心是一個點(diǎn),

10、算作第一層, 第2層每邊有2個點(diǎn),第3層每邊有3個點(diǎn) ,…, 第層每邊有個點(diǎn), 則這個點(diǎn)陣的點(diǎn)數(shù)共有 個. 15．在平面內(nèi)有≥條直線，其中任何兩條不平行，任何三條不過同一點(diǎn)，若這條直線把平面分成個平面區(qū)域，則的表達(dá)式是 ． 16．給出下列不等式： , ， ， ………… 則按此規(guī)律可猜想第個不等式為 . 三、解答題：本大題共6小題，滿分70分． 17．（本小題滿分10分） 用分析法證明：． 18．（本小題滿分12分） 用反證法證明：已知，且，求證：與中至少有一個小于．

11、 19．（本小題滿分12分） 網(wǎng)絡(luò)購物已經(jīng)被大多數(shù)人接受，隨著時間的推移，網(wǎng)絡(luò)購物的人越來越多，然而也有部分人對網(wǎng)絡(luò)購物的質(zhì)量和信譽(yù)產(chǎn)生懷疑．對此，某新聞媒體進(jìn)行了調(diào)查，在所有參與 調(diào)查的人中，持“支持”和“不支持”態(tài)度的人數(shù)如下表所示： 年齡 態(tài)度 支持 不支持 20歲以上50歲以下 800 200 50歲以上（含50歲） 100 300 （1）在所有參與調(diào)查的人中，用分層抽樣的方法抽取個人，已知從持“支持”態(tài)度的人中抽取了9人，求的值； （2）是否有99.9%的的把握認(rèn)為支持網(wǎng)絡(luò)購物與年齡有關(guān)？ 20．(本小題滿分12分)

12、 某企業(yè)為了對生產(chǎn)的一種新產(chǎn)品進(jìn)行合理定價，將該產(chǎn)品按事先擬定的價格進(jìn)行試銷，得到以下數(shù)據(jù)： 單價x（元/件） 60 62 64 66 68 70 銷量y（件） 91 84 81 75 70 67 （Ⅰ）畫出散點(diǎn)圖，并求關(guān)于的回歸方程； （Ⅱ）已知該產(chǎn)品的成本是36元/件，預(yù)計(jì)在今后的銷售中，銷量與單價仍然服從（Ⅰ）中的關(guān)系，為使企業(yè)獲得最大利潤，該產(chǎn)品的單價應(yīng)定為多少元（精確到元）？ 21.（本小題滿分12分） 已知橢圓具有性質(zhì):若是橢圓上關(guān)于原點(diǎn)對稱的兩個點(diǎn),點(diǎn)是橢圓上任意一點(diǎn),且直線的斜

13、率都存在(記為),則是與點(diǎn)位置無關(guān)的定值.試寫出雙曲線的類似性質(zhì),并加以證明. F1 A x y O F2 22.（本小題滿分12分） 已知：； .通過觀察上述兩等式的規(guī)律，請你寫出對任意角度都成立的一般性的命題，并給予證明． xx第二學(xué)期第一次月考 高二年級實(shí)驗(yàn)班(文科數(shù)學(xué))試題 參考答案 一、選擇題：本大題每小題5分，滿分60分． 1 2 3 4 5 6 7 8 9 10 11 12 D B C D C B D C B B A A 二、填

14、空題：本大題每小題5分；滿分20分． 13．. 14．. 15．．16．． 三、解答題： 17．（本小題滿分10分） 用分析法證明：. 證明：要證， 只需證 只需證 只需證 只需證 只需證，此式顯然成立． 由于以上過程步步可逆，故原不等式成立. 18．（本小題滿分12分） 用反證法證明：已知，且，求證：與中至少有一個小于． 證明：假設(shè)和都不小于，即,. ∵,∴, 以上兩式相加并整理，得.這與已知條件矛盾，這說明假設(shè)不正確， 故原結(jié)論成立. 19．（本小題滿分10分） 網(wǎng)絡(luò)購物已經(jīng)被大多數(shù)人接受，隨著時間的推移，網(wǎng)絡(luò)購物的人越來越多，然而

15、也有部分人對網(wǎng)絡(luò)購物的質(zhì)量和信譽(yù)產(chǎn)生懷疑．對此，某新聞媒體進(jìn)行了調(diào)查，在所有參與 調(diào)查的人中，持“支持”和“不支持”態(tài)度的人數(shù)如下表所示： 年齡 態(tài)度 支持 不支持 20歲以上50歲以下 800 200 50歲以上（含50歲） 100 300 （1）在所有參與調(diào)查的人中，用分層抽樣的方法抽取個人，已知從持“支持”態(tài)度的人中抽取了9人，求的值； （2）是否有99.9%的的把握認(rèn)為支持網(wǎng)絡(luò)購物與年齡有關(guān)？ 解：（1）由題意，得， 所以．．．．．．．．．．．．．．．．．．．．．．．．．．．．．5分 （2）根據(jù)題意得列聯(lián)表如下， 年齡 態(tài)度 支持 不支持 合計(jì)

16、 20歲以上50歲以下 800 200 1000 50歲以上（含50歲） 100 300 400 合計(jì) 900 500 1400 ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．8分 所以．．．．．．．．．．．．．．．．．．10分 所以有99.9%的把握認(rèn)為是否支持網(wǎng)絡(luò)購物與年齡有關(guān)．．．．．．．．．．．．．．．．．．．．．12分 20．（本小題滿分12分） 某企業(yè)為了對生產(chǎn)的一種新產(chǎn)品進(jìn)行合理定價，將該產(chǎn)品按事先擬定的價格進(jìn)行試銷，得到以下數(shù)據(jù)： 單價x（元/件） 60 62 64 66

17、 68 70 銷量y（件） 91 84 81 75 70 67 （I）畫出散點(diǎn)圖，并求關(guān)于的回歸方程； （II）已知該產(chǎn)品的成本是36元/件，預(yù)計(jì)在今后的銷售中，銷量與單價仍然服從（I）中的關(guān)系，為使企業(yè)獲得最大利潤，該產(chǎn)品的單價應(yīng)定為多少元（精確到元）？ 【解析】（I）散點(diǎn)圖如圖 ……………2分 由圖得銷量與單價線性相關(guān) …………3分 …………4分 ……6分 回歸直線方程為 ……………8分 （II）利潤 ……………10分 當(dāng)時，利潤最大，這時 故定價約為元時，企業(yè)獲得最大利潤.

18、 ……………12分 21．（本小題滿分12分） 已知橢圓具有性質(zhì):若是橢圓上關(guān)于原點(diǎn)對稱的兩個點(diǎn),點(diǎn)是橢圓上任意一點(diǎn),且直線的斜率都存在(記為),則是與點(diǎn)位置無關(guān)的定值.試寫出雙曲線的類似性質(zhì),并加以證明. 解: 雙曲線的類似性質(zhì)為: 若是雙曲線上關(guān)于原點(diǎn)對稱的兩個點(diǎn),點(diǎn)是雙曲線上任意一點(diǎn),且直線的斜率都存在(記為),則是與點(diǎn)位置無關(guān)的定值. 證明如下: 設(shè)點(diǎn)的坐標(biāo)為,則點(diǎn)的坐標(biāo)為,且, 又設(shè)點(diǎn)的坐標(biāo)為,則. 將和 代入上式,得(定值). 22．（本小題滿分12分） 已知：； .通過觀察上述兩等式的規(guī)律，請你寫出對任意角度都成立的一般性的命題，并給予證明. 解：一般形式: 證明如下： 左邊 = = = = = （將一般形式寫成 等均正確.）