《蘇科版八年級(jí)數(shù)學(xué)上冊(cè) 第一章《全等三角形》強(qiáng)化提高測(cè)試卷(無答案)》由會(huì)員分享����,可在線閱讀�,更多相關(guān)《蘇科版八年級(jí)數(shù)學(xué)上冊(cè) 第一章《全等三角形》強(qiáng)化提高測(cè)試卷(無答案)(5頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索�。
1�、 第一章《全等三角形》強(qiáng)化提高測(cè)試卷
時(shí)間:120分鐘 總分120分
一�、 選擇題(每小題3分,共24分)
1. 下列說法:①全等三角形的形狀相同�、大小相等;②全等三角形的對(duì)應(yīng)邊相等����;③全等三角形的對(duì)應(yīng)角相等�;④全等三角形的周長(zhǎng)相等,面積不相等�,其中正確的為(?? )
A. ?①②③④??B.?①②③?????C.?①②④?????D.?①②③④
2.如圖所示的圖形是全等圖形的是(?? )
A.???B.???C.??D.?
3.如圖����,△ABC 是不等邊三角形,DE=BC����,以 D��、E 為兩個(gè)頂點(diǎn)畫
2�����、位置不同的三角形����,使所畫的三角形與△ABC 全等,這樣的三角形最多可畫出( )個(gè)
A.2 B. 3 C. 4 D. 以上結(jié)果均不對(duì)
4.如圖����,點(diǎn) B���、F���、C���、E 在一條直線上,AB∥ED�����,AC∥FD�,那么添加下列一個(gè)條件后�,仍無法判△ABC≌△DEF的是( )
A.∠A=∠D B.AC=DF C.AB=ED D.BF=EC
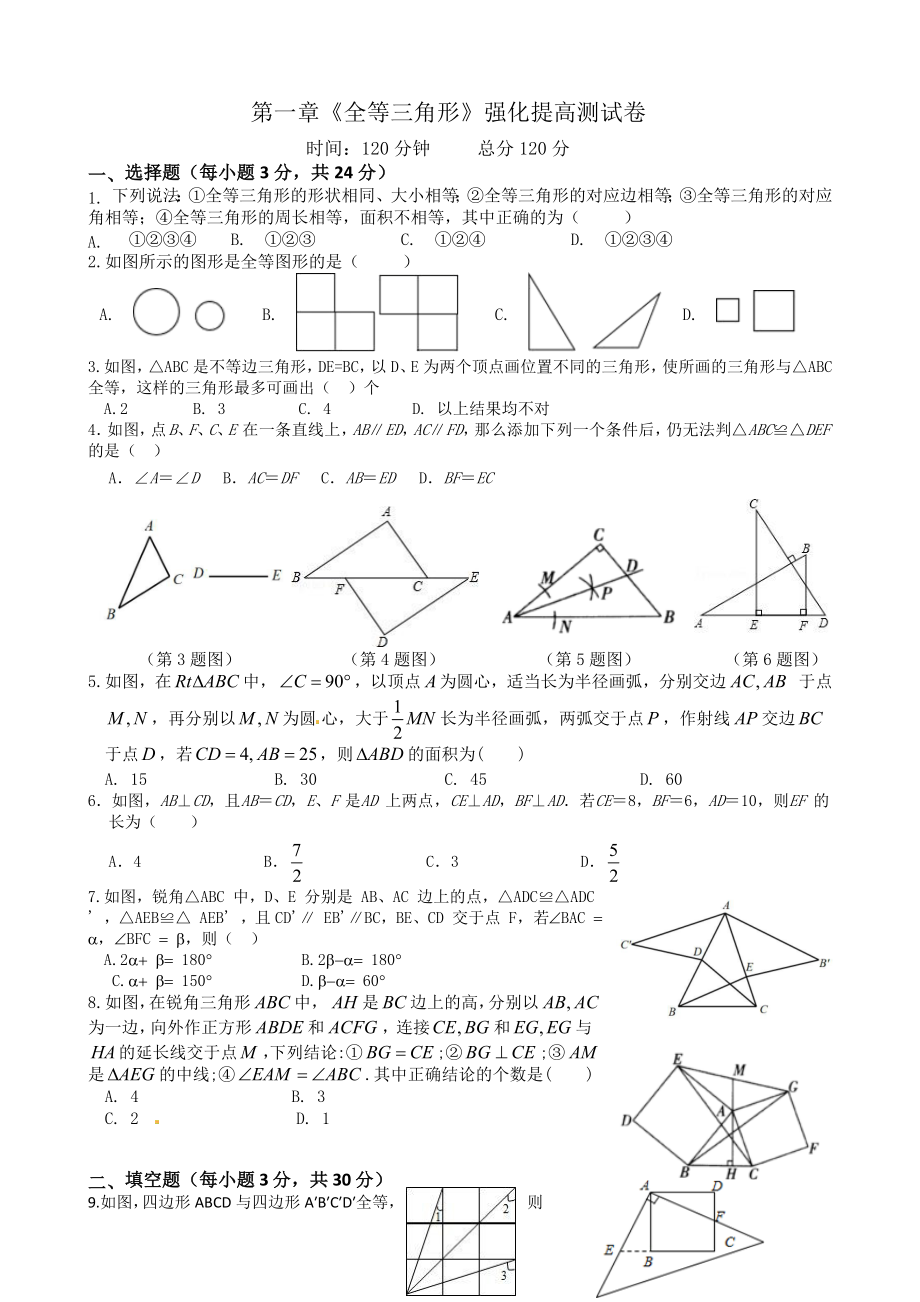
(第3題圖) (第4題圖) (第5題圖) (第6題圖)
5.如圖,在中��,�,以頂點(diǎn)為圓心����,適當(dāng)長(zhǎng)為半徑畫弧,分別交邊 于點(diǎn)����,再分別以為圓心����,
3、大于長(zhǎng)為半徑畫弧���,兩弧交于點(diǎn),作射線交邊于點(diǎn)���,若�����,則的面積為( )
A. 15 B. 30 C. 45 D. 60
6.如圖���,AB⊥CD,且 AB=CD����,E、F 是 AD 上兩點(diǎn)���,CE⊥AD��,BF⊥AD.若 CE=8�,BF=6,AD=10,則 EF 的 長(zhǎng)為( )
A.4 B. C.3 D.
7.如圖����,銳角△ABC 中��,D�����、E 分別是 AB��、AC 邊上的點(diǎn)��,△ADC≌△ADC ' ,△AEB≌△ AEB' ����,且CD'∥ EB'∥BC�����,BE��、CD 交于點(diǎn) F,若DBAC = a��,DBFC =
4�����、b�����,則( )
A.2a+ b= 180° B.2b-a= 180°
C.a+ b= 150° D.b-a= 60°
8.如圖,在銳角三角形中�,是邊上的高���,分別以為一邊,向外作正方形和��,連接和與的延長(zhǎng)線交于點(diǎn)����,下列結(jié)論:①;②;③是的中線;④.其中正確結(jié)論的個(gè)數(shù)是( )
A. 4 B. 3
C. 2 D. 1
二���、 填空題(每小題3分,共30分)
9.如圖���,四邊形ABCD與四邊形A′B′C′D′全等���,則∠A′=__
5、______°�,∠A=________°�,B′C′=________�����,AD=________.
(第9題圖) (第10題圖) (第11題圖)
10.如圖所示的方格中����,∠1+∠2+∠3= 度.
11.如圖����,有一塊邊長(zhǎng)為4的正方形塑料模板ABCD,將一塊足夠大的直角三角板的直角頂點(diǎn)落在A點(diǎn)����,兩條直角邊分別與CD交于點(diǎn)F���,與CB延長(zhǎng)線交于點(diǎn)E.則四邊形AECF的面積是________.
12.如圖,在△ABC 中�����,∠C=90°,在 AB 上截取 AD=AC�����,過點(diǎn) D 作 DE⊥AB��,交 BC 于點(diǎn) E�����,連接 AE
6���、, 已知 BD=2�����,BC=4,則△BDE 的周長(zhǎng)為 .
(第12題圖) (第13題圖) (第14題圖) (第15題圖)
13.如圖���,在△ABC中,AB= AC���,AB>BC,點(diǎn)D在邊BC上��,CD = 4BD,點(diǎn)E����、F在線段AD上,D1=D2=DBAC.若△ABC的面積為40��,則△ACF和△BDE的面積之和為 .
14.如圖,在Rt△ABC中,∠C=90?��,E為AB中點(diǎn),D為AC上一點(diǎn)��,BF//AC交DE的延長(zhǎng)線于點(diǎn)F。AC=6,BC=5,則四邊形FBCD周長(zhǎng)的最小值是_________
7���、__��。
15.如圖��,Rt△ABC中,∠C=90°�,AC=6���,BC=3��,PQ=AB,點(diǎn)P與點(diǎn)Q分別在AC和AC的垂線AD上移動(dòng),則當(dāng)AP=_______,△ABC和△APQ全等��。
16.如圖,是和的平分線的交點(diǎn)�����,且���,垂足為,
=2. 5 cm�����,則與間的距離為 cm.
(第16題圖) (第17題圖) (第18題圖)
17.如圖�,四邊形ABCD中�,AB=AD�����,AC=5����,∠DAB=∠DCB=90°,則四邊形ABCD的面積為 .
18.如圖��,在中����,,點(diǎn)在線段上���,,�,垂足為與相交于點(diǎn).
8��、若= 8 cm,則= cm.
三�����、解答題(共66分)
19.(5分)如圖�,在△ABC和△ADE中���,AB=AD���,∠B=∠D��,∠1=∠2.寫出圖中全等的三角形并證明��。
20.(5分)如圖,點(diǎn)B���、F�����、C、E在同一直線上��,AC�、DF相交于點(diǎn)G�����,AB⊥BE�����,垂足為B��,DE⊥BE��, 垂足為 E�����,且AC=DF,BF=CE.
(1)求證:△ABC≌△DEF����;
(2)若DA=65°����,求DAGF的度數(shù).
21.(7分)已知:△ABC≌△EDC.
(1)若 DE∥BC(如圖 1)����,判斷△ABC 的形狀并說明
9�����、理由.
(2)連結(jié) BE���,交 AC 于 F��,點(diǎn) H 是 CE 上的點(diǎn)����,且 CH=CF����,連結(jié) DH 交 BE 于 K(如圖 2).求證:
∠DKF=∠ACB
22.(7分)如圖,在△ABC中���,D是BC的中點(diǎn),過D點(diǎn)的直線EG交AB于點(diǎn)E�,交AB的平行線CG于點(diǎn)G,DF⊥EG���,交AC于點(diǎn)F.
(1)求證:BE=CG���;
(2)判斷BE+CF與EF的大小關(guān)系���,并證明你的結(jié)論.
23.(8分)已知�,在△ABC中,∠B=∠C���,AB=12cm�����,BC=10cm�,點(diǎn)D是AB的中
10�����、點(diǎn)���,點(diǎn)P在線段BC上以2cm/s的速度由點(diǎn)B向點(diǎn)C運(yùn)動(dòng)��,同時(shí)點(diǎn)Q在線段CA上以相同的速度由點(diǎn)C向點(diǎn)A運(yùn)動(dòng)�,當(dāng)一個(gè)點(diǎn)到達(dá)終點(diǎn)時(shí)另一個(gè)點(diǎn)也隨之停止運(yùn)動(dòng).當(dāng)△BPD和△CQP全等時(shí)����,求點(diǎn)P運(yùn)動(dòng)的時(shí)間.
24.(10分)已知△ABC中,AB=AC=BC=6.點(diǎn)P射線BA上一點(diǎn)����,點(diǎn)Q是AC的延長(zhǎng)線上一點(diǎn)�����,且BP=CQ�����,連接PQ�����,與直線BC相交于點(diǎn)D.
(1)如圖①�����,當(dāng)點(diǎn)P為AB的中點(diǎn)時(shí)����,求CD的長(zhǎng)����;
(2)如圖②����,過點(diǎn)P作直線BC的垂線,垂足為E�,當(dāng)點(diǎn)P,Q分別在射線BA和AC的延長(zhǎng)線上任意地移動(dòng)過
11�、程中,線段BE�����,DE�,CD中是否存在長(zhǎng)度保持不變的線段?請(qǐng)說明理由.
25.(12分)八年級(jí)一班數(shù)學(xué)興趣小組在一次活動(dòng)中進(jìn)行了探究試驗(yàn)活動(dòng)�����,請(qǐng)你和他們一起活動(dòng)吧.
【探究與發(fā)現(xiàn)】
(1)如圖 1����,AD 是三角形 ABC 的中線,延長(zhǎng) AD 至點(diǎn) E�,使 ED=AD,連接 BE�����,請(qǐng)寫出圖中全等的兩個(gè)三角形并證明;
【理解與應(yīng)用】
(2)填空:如圖 2�����,EP 是△DEF 的中線��,若 EF=5��,DE=3���,設(shè) EP=x�,則 x 的取值范圍是 .
(3)已知:如圖 3�����,AD 是△ABC 的中點(diǎn)�,∠BAC=∠ACB,點(diǎn) Q 在 BC 的延長(zhǎng)線上�,QC=BC. 求證:AQ=2AD.
26. (12分)(1)觀察推理:如圖①,在中�����,,直線過點(diǎn)���,點(diǎn)在直線的同側(cè)�����,��,垂足分別為.求證:.
(2)類比探究:如圖②�,在中��,��,將斜邊繞點(diǎn)逆時(shí)針旋轉(zhuǎn)90°至����,連接�����,求的面積.
(3)拓展提升:如圖③,在中����,�,點(diǎn)在上����,且�,動(dòng)點(diǎn)從點(diǎn)沿射線以每秒1個(gè)單位長(zhǎng)度的速度運(yùn)動(dòng)�,連接��,將線段繞點(diǎn)逆時(shí)針旋轉(zhuǎn)120°得到線段.要使點(diǎn)恰好落在射線上�����,求點(diǎn)運(yùn)動(dòng)的時(shí)間.
5 / 5
 蘇科版八年級(jí)數(shù)學(xué)上冊(cè) 第一章《全等三角形》強(qiáng)化提高測(cè)試卷(無答案)
蘇科版八年級(jí)數(shù)學(xué)上冊(cè) 第一章《全等三角形》強(qiáng)化提高測(cè)試卷(無答案)