2022屆江西省宜春市上高二中高三上學(xué)期第五次月考試題 數(shù)學(xué)（理）含答案

《2022屆江西省宜春市上高二中高三上學(xué)期第五次月考試題 數(shù)學(xué)（理）含答案》由會員分享，可在線閱讀，更多相關(guān)《2022屆江西省宜春市上高二中高三上學(xué)期第五次月考試題 數(shù)學(xué)（理）含答案（14頁珍藏版）》請在裝配圖網(wǎng)上搜索。

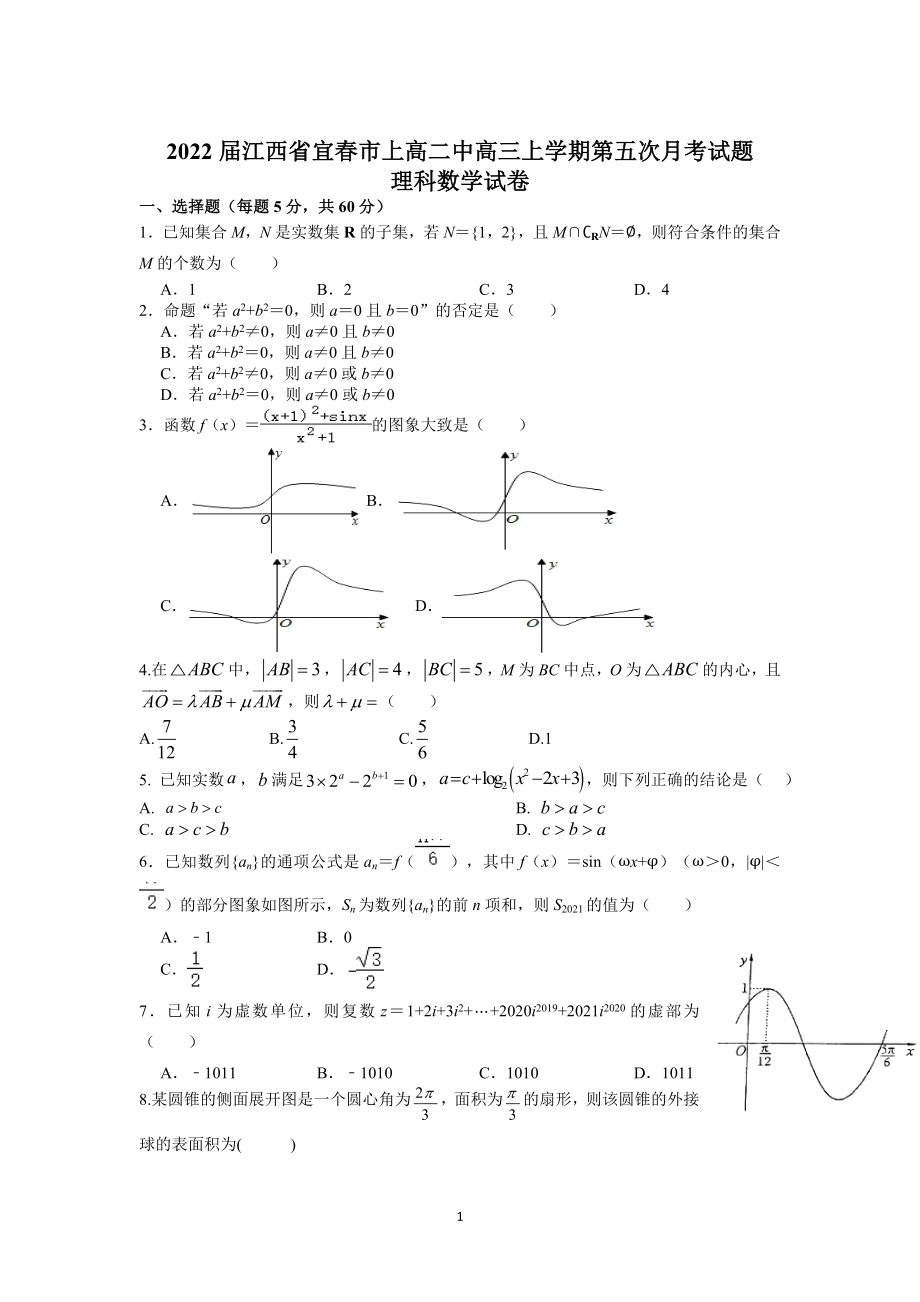
1、 2022屆江西省宜春市上高二中高三上學(xué)期第五次月考試題 理科數(shù)學(xué)試卷 一、選擇題（每題5分，共60分） 1．已知集合M，N是實數(shù)集R的子集，若N＝{1，2}，且M∩?RN＝?，則符合條件的集合M的個數(shù)為（　?。? A．1 B．2 C．3 D．4 2．命題“若a2+b2＝0，則a＝0且b＝0”的否定是（　　） A．若a2+b2≠0，則a≠0且b≠0 B．若a2+b2＝0，則a≠0且b≠0 C．若a2+b2≠0，則a≠0或b≠0 D．若a2+b2＝0，則a≠0或b≠0 3．函數(shù)f（x）＝的圖象大致是（　?。? A． B． C． D． 4.在中，，，，M為B

2、C中點，O為的內(nèi)心，且，則（ ） A. B. C. D.1 5. 已知實數(shù)，滿足，，則下列正確的結(jié)論是（ ） A. B. C. D. 6．已知數(shù)列{an}的通項公式是an＝f（），其中f（x）＝sin（ωx+φ）（ω＞0，|φ|＜）的部分圖象如圖所示，Sn為數(shù)列{an}的前n項和，則S2021的值為（　?。? A．﹣1 B．0 C． D． 7．已知i為虛數(shù)單位，則復(fù)數(shù)z＝1+2i+3i2+?+2020i2019+2021i2020的虛部為（　?。? A．﹣1011 B．﹣1010 C．1010 D．1011 8.某圓錐的側(cè)面展開圖是一個圓心角為

3、，面積為的扇形，則該圓錐的外接球的表面積為( ) A. B. C. D. 9. 在數(shù)1和3之間插入n個實數(shù)，使得這n＋2個數(shù)構(gòu)成等差數(shù)列，將這n＋2個數(shù)的和記為bn，則數(shù)列的前78項和為(　　) A. 3 B. log378 C. 5 D. log38 10．如圖，A，B，C是半徑為1的圓周上的點，且， ，則圖中陰影區(qū)域的面積為（　　） A． B． C． D． 11. 已知函數(shù)與直線在第一象限的交點橫坐標(biāo)從小到大依次分別為，則（ ） A. B. 0 C. 1 D. 12．已知函數(shù)，，若對于任意的

4、，存在唯一的，使得，則實數(shù)a的取值范圍是（ ） A． B． C． D． 二、填空題（每題5分，共20分） 13．已知＝（1，2），＝（0，﹣1），則在方向上的投影為　 　． 14. 等比數(shù)列前n項和為，若，，則________． 15. 已知實數(shù)，滿足，則的取值范圍是_______． 16．已知函數(shù)，若關(guān)于x的不等式在R上恒成立，則實數(shù)a的取值范圍是________ ． 三、解答題(共70分) 17.( 本小題10分)在直角坐標(biāo)系xOy中，曲線C的參數(shù)方程為(φ為參數(shù))，直線l的參數(shù)方程為(t為參數(shù)，0≤α<π)。 (I)若曲線C與y

5、軸負(fù)半軸的交點在直線l上，求α； (II)若tanα＝，求曲線C上與直線l距離最大的點的坐標(biāo)。 18.( 本小題12分)已知函數(shù)f(x)＝|x＋1|＋|2x－5|－7。 (I)在如圖所示的網(wǎng)格中畫出y＝f(x)的圖象； (II)若當(dāng)x<1時，f(x)>f(x＋a)恒成立，求a的取值范圍。 19. (本小題12分)在中，角A，B，C的對邊分別為a，b，c，且 ， （1）求角B的大??； （2）已知點D滿足，且，若，，求AC. 20．(本小題12分)已知等比數(shù)列{an}滿足條件a2+a4＝3（a1+a3），a2n＝3

6、an2，n∈N*，數(shù)列{bn}滿足b1＝1，bn﹣bn﹣1＝2n﹣1（n≥2，n∈N*） （1）求數(shù)列{an}，{bn}的通項公式； （2）若數(shù)列{cn}滿足，n∈N*，求{cn}的前n項和Tn． 21．(本小題12分)在如圖所示的幾何體中，EA⊥平面ABCD，四邊形ABCD為等腰梯形，AD∥BC，AD＝BC，AD＝1，∠ABC＝60°，EF∥AC，EF＝AC． （1）證明：AB⊥CF； （2）當(dāng)二面角B﹣EF﹣D的余弦值為時，求線段CF的長． 22. (本小題12分)已知函數(shù)在點處的切線方程為. （Ⅰ）求的單調(diào)區(qū)間； （

7、Ⅱ）設(shè)是函數(shù)的兩個零點，求證：. 2022屆高三年級第五次月考理科數(shù)學(xué)試卷答題卡 一、選擇題（每小題5分，共60分） 1 2 3 4 5 6 7 8 9 10 11 12 二、填空題（本大題共4個小題，每小題5，共20分） 13、 14、 15、 16、 三、解答題（共70分） 17．(10分)

8、 18. (12分) 19. (12分) 20.(12分)

9、 21. (12分) 22. (12分) 2022屆高三年級第五次月考理科數(shù)學(xué)試卷答案 DDBAB

10、 DBCAA DB 13. ﹣2 14. 15. 16. 17. 18. 19. 解（1）因為A，B，C是三角形ABC的內(nèi)角，所以， 由，得， 即， 化簡得，解得或（舍）， 因為，所以. （2）因為，所以， 在中，，所以， 又，所以，，， 所以，所以. 20. 解：（1）設(shè){an}的通項公式為，n∈N*， 由已知a2+a4＝3（a1+a3），，得q＝3， 由已知，即，解得q＝3a1，a1＝1， 所以 {an}的通項公式為． 因為b1＝1，bn﹣bn﹣1＝2n﹣1（n≥2，n∈N*）， 累加可得． （2）當(dāng)n＝1時，，c1＝1，

11、 當(dāng)n≥2時，①， ②， 由①﹣②得到，，n≥2， 綜上，，n∈N*.③， ④， 由③﹣④得到， 所以． 21. 【解答】證明：（1）由題意，EA⊥平面ABCD，又AB?平面ABCD， ∴AB⊥AE， 過點A作AH⊥BC于點H，在Rt△ABH中， ∵∠ABH＝60°，BH＝，∴AB＝1， 在△ABC中，AC2＝AB2+BC2﹣2AB?BC?cos60°＝， ∴AB2+AC2＝BC2，則AB⊥AC， 又AC∩AE＝A，∴AB⊥平面ACE， 而CF?平面ACE，∴AB⊥CF； 解：（2）以A為坐標(biāo)原點，分別以AB、AC、AE所在直線為x、y、z軸建立空間直角坐標(biāo)系， 設(shè)AE＝a（a＞0），則B（1，0，0），E（0，0，a），F(xiàn)（0，，a），D（，，0）， ∴，，，， 設(shè)平面BEF的一個法向量為， 由，取x＝a，得； 設(shè)平面DEF的一個法向量為， 由，取z1＝﹣1，得． |cos＜＞|＝||＝||＝， 整理得4a4﹣5a2+1＝0，解得a＝1或a＝． ∵二面角B﹣EF﹣D為銳二面角，經(jīng)檢驗a＝舍去，∴a＝1． 作FM⊥AC于M，則M為AC的中點， ∴CF＝． 14