高考數(shù)學(xué)復(fù)習(xí) 17-18版 第5章 第22課 同角三角函數(shù)的基本關(guān)系及誘導(dǎo)公式

《高考數(shù)學(xué)復(fù)習(xí) 17-18版 第5章 第22課 同角三角函數(shù)的基本關(guān)系及誘導(dǎo)公式》由會(huì)員分享，可在線閱讀，更多相關(guān)《高考數(shù)學(xué)復(fù)習(xí) 17-18版 第5章 第22課 同角三角函數(shù)的基本關(guān)系及誘導(dǎo)公式（14頁珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

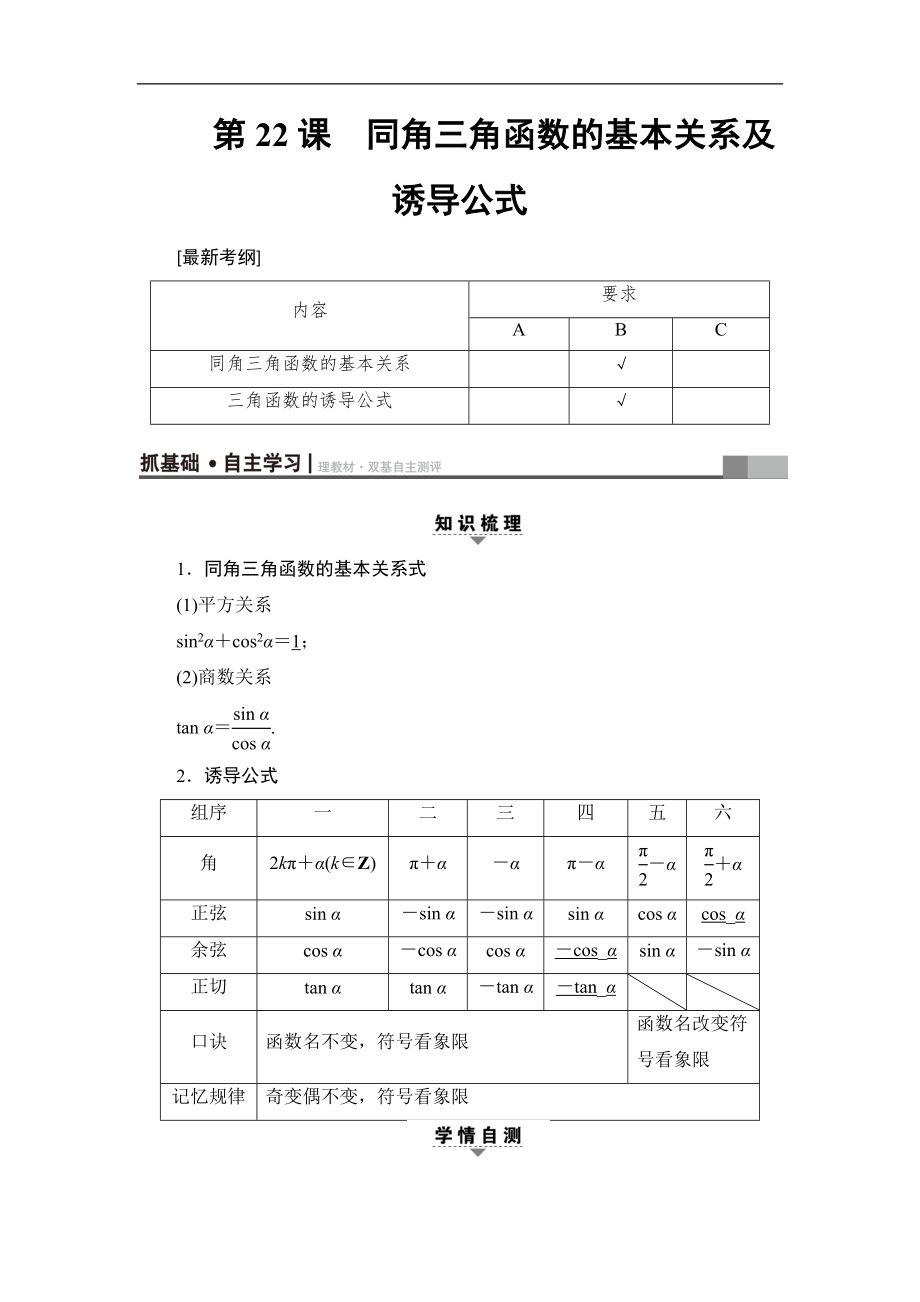
1、 第22課 同角三角函數(shù)的基本關(guān)系及誘導(dǎo)公式 [最新考綱] 內(nèi)容 要求 A B C 同角三角函數(shù)的基本關(guān)系 √ 三角函數(shù)的誘導(dǎo)公式 √ 1．同角三角函數(shù)的基本關(guān)系式 (1)平方關(guān)系 sin2α＋cos2α＝1； (2)商數(shù)關(guān)系 tan α＝. 2．誘導(dǎo)公式 組序 一 二 三 四 五 六 角 2kπ＋α(k∈Z) π＋α －α π－α －α ＋α 正弦 sin α －sin α －sin α sin α cos α cos_α 余弦 cos α －cos α cos α －cos_α

2、 sin α －sin α 正切 tan α tan α －tan α －tan_α 口訣 函數(shù)名不變，符號(hào)看象限 函數(shù)名改變符號(hào)看象限 記憶規(guī)律 奇變偶不變，符號(hào)看象限 1．(思考辨析)判斷下列結(jié)論的正誤．(正確的打“√”，錯(cuò)誤的打“×”) (1)若α，β為銳角，則sin2α＋cos2β＝1.(　　) (2)若α∈R，則tan α＝恒成立．(　　) (3)sin(π＋α)＝－sin α成立的條件是α為銳角．(　　) (4)誘導(dǎo)公式的記憶口訣中“奇變偶不變，符號(hào)看象限”，其中的奇、偶是指的奇數(shù)倍、偶數(shù)倍，變與不變指函數(shù)名稱是否變化．(　　) [答案

3、]　(1)×　(2)×　(3)×　(4)√ 2．(教材改編)已知α是第二象限角，sin α＝，則cos α等于________． －　[∵sin α＝，α是第二象限角， ∴cos α＝－＝－.] 3．若tan α＝，則sin4α－cos4α的值為________． －　[sin4α－cos4α＝(sin2α－cos2α)(sin2α＋cos2α)＝＝＝－.] 4．(2016·四川高考)sin 750°＝________. 　[sin 750°＝sin(750°－360°×2)＝sin 30°＝.] 5．已知sin＝，α∈，則sin(π＋α)＝________. －　[因?yàn)閟i

4、n＝cos α＝，α∈，所以sin α＝＝，所以sin(π＋α)＝－sin α＝－.] 同角三角函數(shù)基本關(guān)系式的應(yīng)用 　(1)已知sin αcos α＝，且＜α＜，則cos α－sin α的值為________． (2)(2016·全國卷Ⅲ改編)若tan α＝，則cos2α＋2sin 2α＝________. (1)　(2)　[(1)∵＜α＜， ∴cos α＜0，sin α＜0且cos α＞sin α， ∴cos α－sin α＞0. 又(cos α－sin α)2＝1－2sin αcos α＝1－2×＝， ∴cos α－sin α＝. (2)∵tan α＝，則c

5、os2α＋2sin 2α＝＝＝＝.] [規(guī)律方法]　1.利用sin2α＋cos2α＝1可以實(shí)現(xiàn)角α的正弦、余弦的互化，利用＝tan α可以實(shí)現(xiàn)角α的弦切互化． 2．應(yīng)用公式時(shí)要注意方程思想的應(yīng)用：對(duì)于sin α＋cos α，sin αcos α，sin α－cos α這三個(gè)式子，利用(sin α±cos α)2＝1±2sin αcos α，可以知一求二． 3．注意公式逆用及變形應(yīng)用：1＝sin2α＋cos2α，sin2α＝1－cos2α，cos2α＝1－sin2α. [變式訓(xùn)練1]　(1)已知sin α－cos α＝，α∈(0，π)，則tan α等于________. 【導(dǎo)學(xué)號(hào)：6

6、2172123】 －1　[由 消去sin α得：2cos2α＋2cos α＋1＝0， 即(cos α＋1)2＝0， ∴cos α＝－. 又α∈(0，π)，∴α＝， ∴tan α＝tan＝－1.] (2)設(shè)θ為第二象限角，若tan＝，則sin θ＋cos θ＝________. －　[∵tan＝，∴＝，解得tan θ＝－. ∴(sin θ＋cos θ)2＝ ＝＝＝. ∵θ為第二象限角，tan θ＝－， ∴2kπ＋＜θ＜2kπ＋π，∴sin θ＋cos θ＜0， ∴sin θ＋cos θ＝－.] 誘導(dǎo)公式的應(yīng)用 　(1)已知A＝＋(k∈Z)，則A的值構(gòu)成的集合是_

7、_______． (2)(2017·南通一模)已知sin＝，則sin＋sin2的值是________． (1){－2,2}　(2)　[(1)當(dāng)k為偶數(shù)時(shí)，A＝＋＝2； k為奇數(shù)時(shí)，A＝－＝－2. (2)sin＋sin2＝sin＋sin2＝－sin＋1－sin2＝.] [規(guī)律方法]　1.利用誘導(dǎo)公式應(yīng)注意已知角或函數(shù)名稱與所求角或函數(shù)名稱之間存在的關(guān)系，尤其是角之間的互余、互補(bǔ)關(guān)系，選擇恰當(dāng)?shù)墓?，向所求角和三角函?shù)進(jìn)行化歸． 2．誘導(dǎo)公式的應(yīng)用原則：負(fù)化正、大化小、小化銳、銳求值． [變式訓(xùn)練2]　已知cos＝，則cos－sin2的值為________. 【導(dǎo)學(xué)號(hào)：6217212

8、4】 －　[∵cos＝cos ＝－cos＝－， sin2＝sin2＝sin2 ＝1－cos2＝1－2＝， ∴cos－sin2＝－－＝－.] 同角關(guān)系式與誘導(dǎo)公式的綜合應(yīng)用 　(1)(2016·全國卷Ⅰ)已知θ是第四象限角，且sin＝，則tan＝________. (2)(2017·南京模擬)已知cos＝2sin，則的值為________． (1)－　(2)　[(1)由題意知sin＝，θ是第四象限角，所以cos＞0，所以cos＝＝. tan＝tan＝－ ＝－＝－＝－. (2)∵cos＝2sin， ∴－sin α＝－2cos α，則sin α＝2cos α， 代入s

9、in2α＋cos2α＝1，得cos2α＝. ＝ ＝＝cos2α－＝.] [規(guī)律方法]　利用同角三角函數(shù)基本關(guān)系式和誘導(dǎo)公式化簡三角函數(shù)的基本思路和化簡要求：(1)基本思路：①分析結(jié)構(gòu)特點(diǎn)，選擇恰當(dāng)公式；②利用公式化成單角三角函數(shù)；③整理得最簡形式． (2)化簡要求：①化簡過程是恒等變形；②結(jié)果要求項(xiàng)數(shù)盡可能少，次數(shù)盡可能低，結(jié)構(gòu)盡可能簡單，能求值的要求出值． [變式訓(xùn)練3]　已知sin α＝，α是第二象限角，則tan(π－α)＝________. 　[∵sin α＝，α是第二象限角， ∴cos α＝－， ∴tan α＝－，故tan(π－α)＝－tan α＝.] [思想與方

10、法] 三角函數(shù)求值與化簡的常用方法 (1)弦切互化法：主要利用公式tan α＝進(jìn)行弦、切互化． (2)和積轉(zhuǎn)換法：利用(sin θ±cos θ)2＝1±2sin θcos θ的關(guān)系進(jìn)行變形、轉(zhuǎn)化． (3)巧用“1”的變換：1＝sin2θ＋cos2θ＝cos2θ(1＋tan2θ)＝tan等． (4)利用相關(guān)角的互補(bǔ)、互余等特殊關(guān)系可簡化解題步驟． [易錯(cuò)與防范] 1．利用誘導(dǎo)公式進(jìn)行化簡求值時(shí)，先利用公式化任意角的三角函數(shù)為銳角三角函數(shù)，其步驟：去負(fù)—脫周—化銳．應(yīng)特別注意函數(shù)名稱和符號(hào)的確定． 2．在利用同角三角函數(shù)的平方關(guān)系時(shí)，若開方，要特別注意判斷符號(hào)． 課時(shí)分層訓(xùn)練(二

11、十二) A組　基礎(chǔ)達(dá)標(biāo) (建議用時(shí)：30分鐘) 一、填空題 1．若cos α＝，α∈，則tan α等于________． －2　[∵α∈， ∴sin α＝－＝－＝－， ∴tan α＝＝－2.] 2．已知sin(π＋θ)＝－cos(2π－θ)，|θ|＜，則θ等于________. 【導(dǎo)學(xué)號(hào)：62172125】 　[∵sin(π＋θ)＝－cos(2π－θ)， ∴－sin θ＝－cos θ，∴tan θ＝.∵|θ|＜，∴θ＝.] 3．(2017·蘇州期中)已知sin α＝，且α∈，則tan α＝________. －　[∵α∈，sin α＝，∴cos α＝－＝－. ∴t

12、an α＝＝－.] 4．若sin＝，則cos＝________. 　[cos＝cos ＝sin＝.] 5．已知α是三角形的內(nèi)角，且sin α＋cos α＝，則tan α＝________. 【導(dǎo)學(xué)號(hào)：62172126】 －　[由 消去cos α整理，得 25sin2α－5sin α－12＝0， 解得sin α＝或sin α＝－. 因?yàn)棣潦侨切蔚膬?nèi)角， 所以sin α＝. 又由sin α＋cos α＝，得cos α＝－， 所以tan α＝－.] 6．已知α為第二象限角，則cos α＋sin α·＝________. 0　[原式＝cos α＋sin α ＝cos

13、 α＋sin α ＝cos α＋sin α ＝0.] 7．sin21°＋sin22°＋sin23°＋…＋sin289°＝________. 44．5　[因?yàn)閟in(90°－α)＝cos α，所以當(dāng)α＋β＝90°時(shí)，sin2α＋sin2β＝sin2α＋cos2α＝1， 設(shè)S＝sin21°＋sin22°＋sin23°＋…＋sin289°， 則S＝sin289°＋sin288°＋sin287°＋…＋sin21° 兩個(gè)式子相加得2S＝1＋1＋1＋…＋1＝89，S＝44.5.] 8．(2017·蘇北四市調(diào)研)＝________. 　[原式＝＝ ＝ ＝.] 9．已知sin θ＋co

14、s θ＝，則sin θ－cos θ的值為________. 【導(dǎo)學(xué)號(hào)：62172127】 －　[∵sin θ＋cos θ＝， ∴1＋2sin θcos θ＝， ∴2sin θcos θ＝.又0＜θ＜， 故sin θ－cos θ＝－＝ －＝－.] 10．已知角θ的頂點(diǎn)在坐標(biāo)原點(diǎn)，始邊與x軸正半軸重合，終邊在直線2x－y＝0上，則＝________. 2　[由題意可得tan θ＝2， 原式＝＝＝2.] 二、解答題 11．求值：sin(－1 200°)·cos 1 290°＋cos(－1 020°)·sin(－1 050°)＋tan 945°. [解]　原式＝－sin 1

15、200°·cos 1 290°＋cos 1 020°·(－sin 1 050°)＋tan 945° ＝－sin 120°·cos 210°＋cos 300°·(－sin 330°)＋tan 225° ＝(－sin 60°)·(－cos 30°)＋cos 60°·sin 30°＋tan 45° ＝×＋×＋1＝2. 12．已知sin(3π＋α)＝2sin，求下列各式的值： (1)； (2)sin2α＋sin 2α. [解]　由已知得sin α＝2cos α. (1)原式＝＝－. (2)原式＝ ＝＝. B組　能力提升 (建議用時(shí)：15分鐘) 1．已知tan x＝sin，則s

16、in x＝________. 　[因?yàn)閠an x＝sin，所以tan x＝cos x，所以sin x＝cos2x，sin2x＋sin x－1＝0，解得sin x＝， 因?yàn)椋?≤sin x≤1，所以sin x＝.] 2．設(shè)函數(shù)f(x)(x∈R)滿足f(x＋π)＝f(x)＋sin x，當(dāng)0≤x＜π時(shí)，f(x)＝0，則f＝________. 　[由f(x＋π)＝f(x)＋sin x，得 f(x＋2π)＝f(x＋π)＋sin(x＋π) ＝f(x)＋sin x－sin x＝f(x)， 所以f＝f ＝f＝f ＝f＋sinπ. 因?yàn)楫?dāng)0≤x＜π時(shí)，f(x)＝0， 所以f＝0＋＝.]

17、3．已知f(α)＝. (1)化簡 f(α)； (2)若α是第三象限角，且cos＝，求f(α)的值． [解]　(1)f(α)＝ ＝ ＝－cos α. (2)∵cos＝－sin α＝， ∴sin α＝－， 又α是第三象限角，∴cos α＝－＝－， 故f(α)＝. 4．已知f(x)＝(n∈Z)． (1)化簡f(x)的表達(dá)式； (2)求f＋f的值． [解]　(1)當(dāng)n為偶數(shù)，即n＝2k(k∈Z)時(shí)， f(x)＝ ＝ ＝ ＝sin2x； 當(dāng)n為奇數(shù)，即n＝2k＋1(k∈Z)時(shí)，f(x)＝＝ ＝＝ ＝sin2x，綜上得f(x)＝sin2x. (2)由(1)得f＋f ＝sin2＋sin2 ＝sin2＋sin2＝sin2＋cos2＝1.