撫順市 專題訓(xùn)練12 幾何證明及通過幾何計(jì)算進(jìn)行說理問題

《撫順市 專題訓(xùn)練12 幾何證明及通過幾何計(jì)算進(jìn)行說理問題》由會(huì)員分享，可在線閱讀，更多相關(guān)《撫順市 專題訓(xùn)練12 幾何證明及通過幾何計(jì)算進(jìn)行說理問題（8頁珍藏版）》請?jiān)谘b配圖網(wǎng)上搜索。

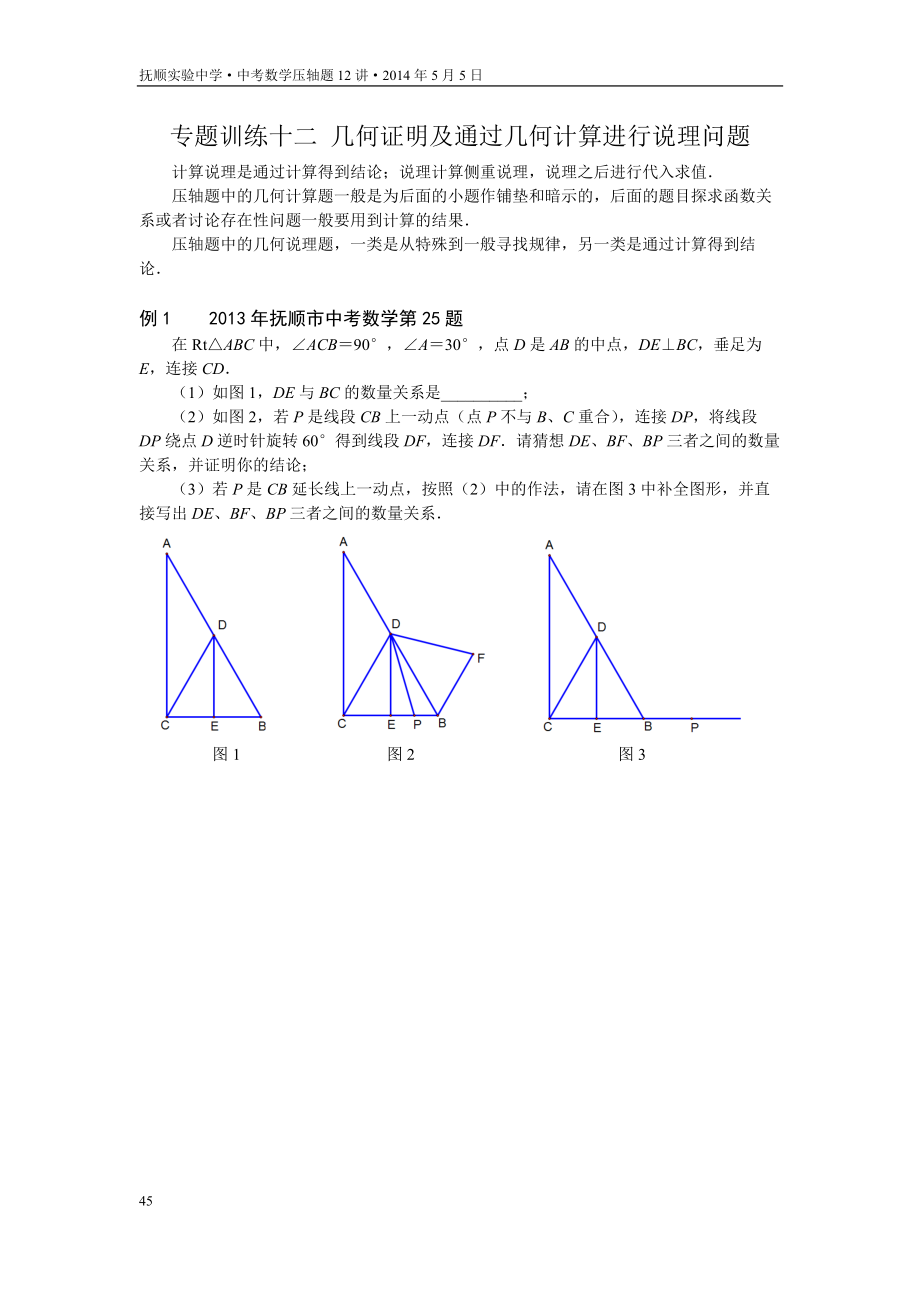
1、撫順實(shí)驗(yàn)中學(xué)·中考數(shù)學(xué)壓軸題12講·2014年5月5日 專題訓(xùn)練十二 幾何證明及通過幾何計(jì)算進(jìn)行說理問題 計(jì)算說理是通過計(jì)算得到結(jié)論；說理計(jì)算側(cè)重說理，說理之后進(jìn)行代入求值． 壓軸題中的幾何計(jì)算題一般是為后面的小題作鋪墊和暗示的，后面的題目探求函數(shù)關(guān)系或者討論存在性問題一般要用到計(jì)算的結(jié)果． 壓軸題中的幾何說理題，一類是從特殊到一般尋找規(guī)律，另一類是通過計(jì)算得到結(jié)論． 例1 2013年撫順市中考數(shù)學(xué)第25題 在Rt△ABC中，∠ACB＝90°，∠A＝30°，點(diǎn)D是AB的中點(diǎn)，DE⊥BC，垂足為E，連接CD． （1）如圖1，DE與BC的數(shù)量關(guān)系是__________；

2、（2）如圖2，若P是線段CB上一動(dòng)點(diǎn)（點(diǎn)P不與B、C重合），連接DP，將線段DP繞點(diǎn)D逆時(shí)針旋轉(zhuǎn)60°得到線段DF，連接DF．請猜想DE、BF、BP三者之間的數(shù)量關(guān)系，并證明你的結(jié)論； （3）若P是CB延長線上一動(dòng)點(diǎn)，按照（2）中的作法，請?jiān)趫D3中補(bǔ)全圖形，并直接寫出DE、BF、BP三者之間的數(shù)量關(guān)系． 圖1 圖2 圖3 例2 2012年撫順市中考數(shù)學(xué)第25題 如圖，在Rt△ABC中，∠ACB＝90°，∠ABC＝30°，點(diǎn)D是直線BC上的一個(gè)動(dòng)點(diǎn)，連接AD，并以AD為邊在AD的右側(cè)作等

3、邊三角形ADE． （1）如圖1，當(dāng)點(diǎn)E恰好在線段BC上時(shí)，請判斷線段DE和BE的數(shù)量關(guān)系，并結(jié)合圖1證明你的結(jié)論； （2）當(dāng)點(diǎn)E不在線段BC上時(shí)，連接BE，其它條件不變，（1）中的結(jié)論是否成立？若成立，請結(jié)合圖2給予證明；若不成立，請直接寫出新的結(jié)論； （3）若AC＝3，點(diǎn)D在直線BC上移動(dòng)的過程中，是否存在以A、C、D、E為頂點(diǎn)的四邊形是梯形？如果存在，直接寫出線段CD的長度；如果不存在，請說明理由． 例3 2012年撫順市中考數(shù)學(xué)第26題 如圖，拋物線的對稱軸是直線x＝2，頂點(diǎn)A的縱坐標(biāo)為1，點(diǎn)B(4, 0)在此拋物線上． （1）求此拋物線的解析式；

4、 （2）若此拋物線的對稱軸與x軸的交點(diǎn)為C，D(x, y)為拋物線上一動(dòng)點(diǎn)，過點(diǎn)D作直線y＝2的垂線，垂足為E． ①用含y的代數(shù)式表示CD2，并猜想CD2與DE2之間的數(shù)量關(guān)系，請給出證明； ②在此拋物線上是否存在點(diǎn)D，使∠EDC＝120°？如果存在，請直接寫出D點(diǎn)坐標(biāo)；如果不存在，請說明理由． 例4 2011年撫順市中考數(shù)學(xué)第25題 如圖，拋物線y＝ax2＋bx－3與x軸交于A(1, 0)、B(3, 0)兩點(diǎn)，與y軸交于點(diǎn)D． （1）求此拋物線的解析式； （2）在拋物線上是否存在一點(diǎn)P，使得△BDP是以BD為斜邊的直角三角形？若存在，請求出點(diǎn)P的坐標(biāo)；若不存

5、在，請說明理由； （3）在x軸下方的拋物線上是否存在點(diǎn)M，過M作MN⊥x軸于點(diǎn)N，使以A、M、N為頂點(diǎn)的三角形與△BCD相似？若存在，求出點(diǎn)M的坐標(biāo)；若不存在，請說明理由． 例5 2014年上海市奉賢區(qū)中考模擬第25題 如圖1，在梯形ABCD中，∠A＝90°，AD//BC， AD＝2，AB＝3， tan∠C＝，點(diǎn)P是AD延長線上一點(diǎn)，F(xiàn)為DC的中點(diǎn)， 聯(lián)結(jié)BP，交線段DF于點(diǎn)G． （1）若以AB為半徑的⊙B與以PD為半徑的⊙P外切，求PD的長； （2）如圖2，過點(diǎn)F作BC的平行線交BP于點(diǎn)E， ①若設(shè)DP＝x，EF＝y(tǒng)，求y與x的函數(shù)關(guān)系式并寫

6、出自變量x的取值范圍； ②聯(lián)結(jié)DE和PF，若DE＝PF，求PD的長． 圖1 圖2 例6 2012年葫蘆島市中考數(shù)學(xué)第25題 △ABC中，BC＝AC＝5，AB＝8，CD為AB邊上的高．如圖1，A在原點(diǎn)處，點(diǎn)B在y軸的正半軸上，點(diǎn)C在第一象限．若A從原點(diǎn)出發(fā)，沿x軸向右以每秒1個(gè)單位長的速度運(yùn)動(dòng)，則點(diǎn)B隨之沿y軸下滑，并帶動(dòng)△ABC在平面上滑動(dòng)．如圖2，設(shè)運(yùn)動(dòng)的時(shí)間為t秒，當(dāng)B到達(dá)原點(diǎn)時(shí)停止運(yùn)動(dòng)． （1）當(dāng)t＝1時(shí)，求點(diǎn)C的坐標(biāo)； （2）當(dāng)t＝4時(shí)，求OD的長及∠BAO的大?。? （3）求從t＝

7、0到t＝4這一段時(shí)間點(diǎn)D運(yùn)動(dòng)路線的長； （4）當(dāng)以點(diǎn)C為圓心、CA為半徑的圓與坐標(biāo)軸相切時(shí)，求t的值． 例7 2011年葫蘆島市中考數(shù)學(xué)第25題 如圖，在直角坐標(biāo)系中，點(diǎn)P的坐標(biāo)是(n,0)(n＞0)，拋物線y＝－x2＋bx＋c經(jīng)過原點(diǎn)O和點(diǎn)P.已知正方形ABCD的三個(gè)頂點(diǎn)為A(2,2)，B(3,2)，D(2,3)． （1）求c，b并寫出拋物線對稱軸及y的最大值(用含有n的代數(shù)式表示)； （2）求證：拋物線的頂點(diǎn)在函數(shù)y＝x2的圖象上； （3）若拋物線與直線AD交于點(diǎn)N，求n為何值時(shí)，△NPO的面積為1； （4）若拋物線經(jīng)過

8、正方形區(qū)域ABCD(含邊界)，請直接寫出n的取值范圍． 例8 2010年葫蘆島市中考數(shù)學(xué)第25題 如圖，在直角梯形ABCD中，AD//BC，∠B＝90°，AD＝6，BC＝8，AB＝．點(diǎn)M是BC的中點(diǎn)，點(diǎn)P從點(diǎn)M出發(fā)沿MB以每秒1個(gè)單位的速度向點(diǎn)B勻速運(yùn)動(dòng)，到達(dá)點(diǎn)B后立刻以原速度沿BC運(yùn)動(dòng)到點(diǎn)C；點(diǎn)Q從點(diǎn)M出發(fā)以每秒1個(gè)單位的速度在射線MC上勻速運(yùn)動(dòng)．在點(diǎn)P、Q的運(yùn)動(dòng)過程中，以PQ為邊作一個(gè)等邊三角形EPQ，使△EPQ與梯形ABCD在射線BC的同側(cè)．點(diǎn)P、Q同時(shí)出發(fā)，當(dāng)點(diǎn)P到達(dá)點(diǎn)C時(shí)停止運(yùn)動(dòng)，點(diǎn)Q也隨之停止．設(shè)點(diǎn)P、Q運(yùn)動(dòng)的時(shí)間為t秒． （1）當(dāng)BP＝2時(shí)，寫出PQ的長； （2）當(dāng)△EPQ的頂點(diǎn)E在AD邊上時(shí)，求出t的取值范圍； （3）是否存在t的值，使得△EPQ的邊經(jīng)過CD的中點(diǎn)O？若存在，請直接寫出t的值；若不存在，請說明理由． 52