《人教版 高中數(shù)學(xué)【選修 21】3.2.3立體幾何中的向量方法：二面角學(xué)案》由會員分享，可在線閱讀，更多相關(guān)《人教版 高中數(shù)學(xué)【選修 21】3.2.3立體幾何中的向量方法：二面角學(xué)案（2頁珍藏版）》請在裝配圖網(wǎng)上搜索。
1、2019人教版精品教學(xué)資料·高中選修數(shù)學(xué)
3.2.3 立體幾何中的向量方法——二面角
【學(xué)習(xí)目標(biāo)】
能用向量方法解決二面角的計算問題.
【自主學(xué)習(xí)】
1. 二面角的大小是用它的平面角來度量的,求二面角關(guān)鍵是確定二面角的平面角.
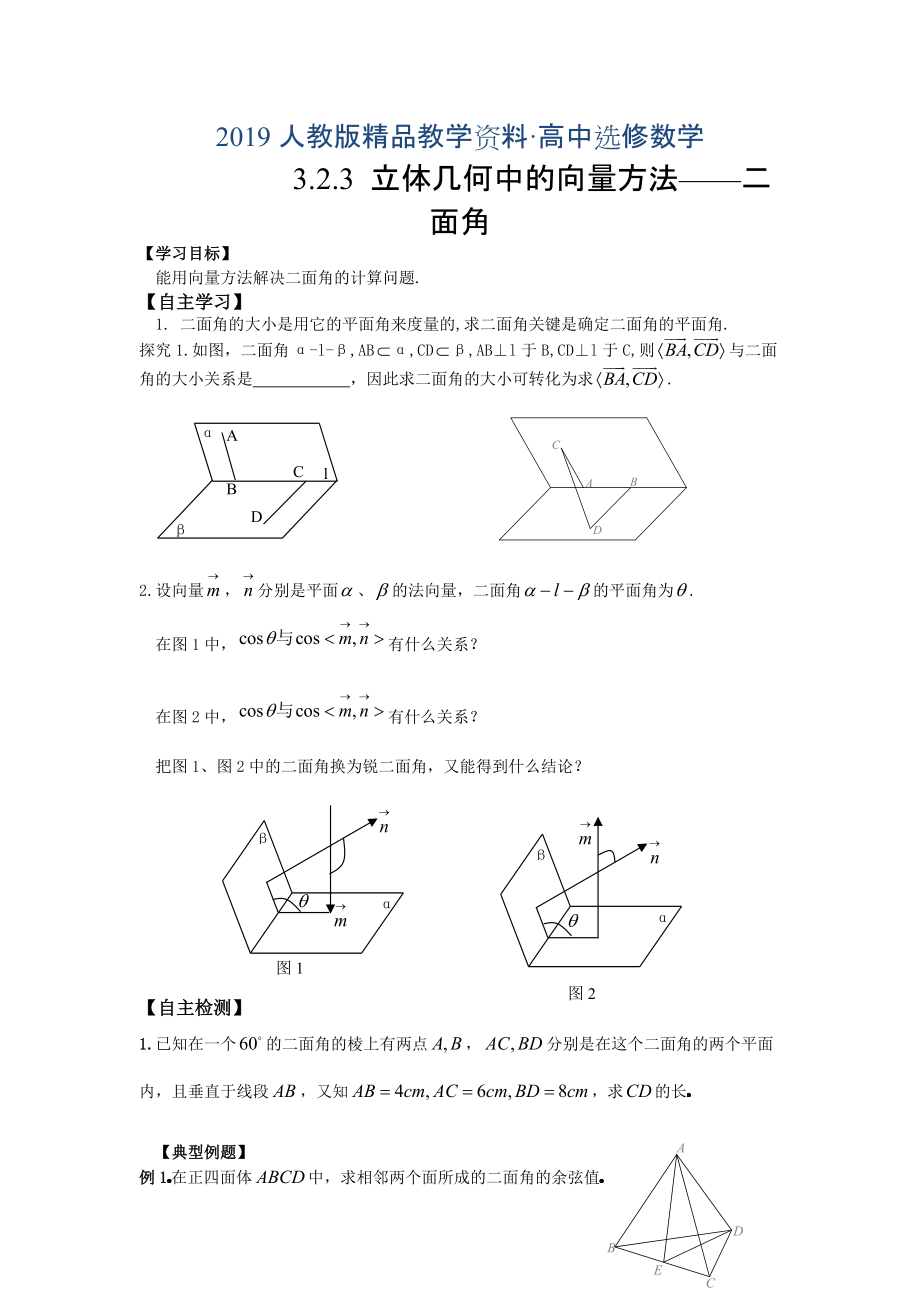
探究1.如圖，二面角α-l-β,ABα,CDβ,AB⊥l于B,CD⊥l于C,則與二面角的大小關(guān)系是 ，因此求二面角的大小可轉(zhuǎn)化為求.
A
B
D
C
l
β
α
2.設(shè)向量，分別是平面、的法向量，二面角的平面角為.
在圖1中，有什么關(guān)系？
在圖2中，有什么關(guān)系？
α
2、
圖2
β
把圖1、圖2中的二面角換為銳二面角，又能得到什么結(jié)論？
β
α
圖1
【自主檢測】
1.已知在一個的二面角的棱上有兩點(diǎn)，分別是在這個二面角的兩個平面內(nèi)，且垂直于線段，又知，求的長
【典型例題】
例1在正四面體中，求相鄰兩個面所成的二面角的余弦值
解：
例2.已知PA垂直矩形ABCD所在平面,PA=AB=1,BC=2,求二面角B-PC-D平面角的余弦值.
解法1：可分別求兩平面的法向量.
解法2：可在兩半平面內(nèi)分別作棱的垂線，求這樣的兩垂線向量的夾角.
A
B
C
D
E
F
P
人教版 高中數(shù)學(xué)【選修 21】3.2.3立體幾何中的向量方法：二面角學(xué)案
