河北省中考數(shù)學總復習 第5章圖形的相似與解直角三角形第2節(jié)銳角三角函數(shù)及解直角三角形的應用中考命題規(guī)律精講試題

《河北省中考數(shù)學總復習 第5章圖形的相似與解直角三角形第2節(jié)銳角三角函數(shù)及解直角三角形的應用中考命題規(guī)律精講試題》由會員分享，可在線閱讀，更多相關《河北省中考數(shù)學總復習 第5章圖形的相似與解直角三角形第2節(jié)銳角三角函數(shù)及解直角三角形的應用中考命題規(guī)律精講試題（7頁珍藏版）》請在裝配圖網(wǎng)上搜索。

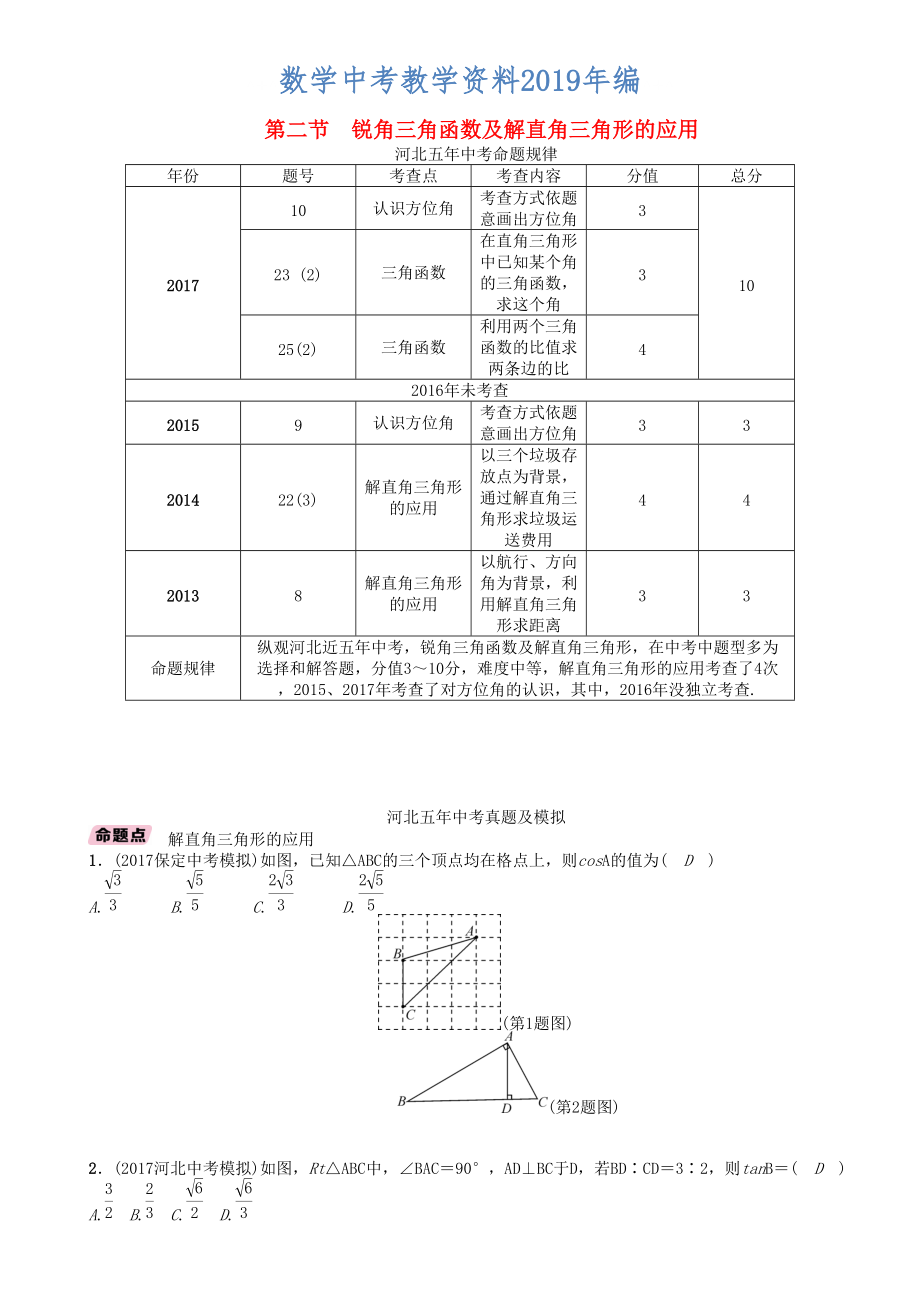
1、△+△數(shù)學中考教學資料2019年編△+△ 第二節(jié)　銳角三角函數(shù)及解直角三角形的應用 河北五年中考命題規(guī)律 年份 題號 考查點 考查內(nèi)容 分值 總分 2017 10 認識方位角 考查方式依題意畫出方位角 3 10 23 (2) 三角函數(shù) 在直角三角形中已知某個角的三角函數(shù)，求這個角 3 25(2) 三角函數(shù) 利用兩個三角函數(shù)的比值求兩條邊的比 4 2016年未考查 2015 9 認識方位角 考查方式依題意畫出方位角 3 3 2014 22(3) 解直角三角形的應用 以三個垃圾存放點為背景，通過解直角三角形求垃圾運送費用 4 4

2、 2013 8 解直角三角形的應用 以航行、方向角為背景，利用解直角三角形求距離 3 3 命題規(guī)律 縱觀河北近五年中考，銳角三角函數(shù)及解直角三角形，在中考中題型多為選擇和解答題，分值3～10分，難度中等，解直角三角形的應用考查了4次，2015、2017年考查了對方位角的認識，其中，2016年沒獨立考查. 河北五年中考真題及模擬 　解直角三角形的應用 1．(2017保定中考模擬)如圖，已知△ABC的三個頂點均在格點上，則cosA的值為(　D　) A.　　　B.　　　C.　　　D. (第1題圖) 　　　　(第2題圖) 2．(2017河北中考

3、模擬)如圖，Rt△ABC中，∠BAC＝90°，AD⊥BC于D，若BD∶CD＝3∶2，則tanB＝(　D　) A. B. C. D. 3．(2016河北中考模擬)在Rt△ABC中，∠C＝90°，如果cosB＝，那么sinA的值是(　B　) A．1 B. C. D. 4．(2016定州中考模擬)如圖，在Rt△ABC中，∠C＝90°，AB＝13，BC＝12.則下列三角函數(shù)表示正確的是(　A　) A．sinA＝　　B．cosA＝ C．tanA＝　　D．tanB＝ 5．(2015河北中考)已知：島P位于島Q的正西方，由島P，Q分別測得船R位

4、于南偏東30°和南偏西45°方向上，符合條件的示意圖是(　D　) ,A) ,B) ,C) ,D) 6．(2013河北中考)如圖，一艘海輪位于燈塔P的南偏東70°方向的M處，它以每小時40海里的速度向正北方向航行，2小時后到達位于燈塔P的北偏東40°的N處，則N處與燈塔P的距離為(　D　) A．40海里 B．60海里 C．70海里 D．80海里 (第6題圖) 　　(第7題圖) 7．(2016保定十三中二模)如圖，港口A在觀測站O的正東方向，OA＝4.某船從港口A出發(fā)，沿北偏東15°方向航行一段距離后到達B處，此時從

5、觀測站O處測得該船位于北偏東60°的方向，則該船航行的距離(即AB的長)為__2__． 8．(2016張家口九中二模)蕪湖長江大橋是中國跨度最大的公路和鐵路兩用橋梁，大橋采用低塔斜拉橋橋型(如圖①)，圖②是從圖①引伸出的平面圖，假設你站在橋上測得拉索AB與水平橋面的夾角是30°，拉索CD與水平橋面的夾角是60°，兩拉索頂端的距離BC為2 m，兩拉索底端距離AD為20 m，請求出立柱BH的長．(結果精確到0.1 m，≈1.732) 解：設DH＝x m. ∵∠CDH＝60°，∠H＝90°， ∴CH＝DH·tan60°

6、＝x， ∴BH＝BC＋CH＝2＋x. ∵∠A＝30°， ∴AH＝BH＝2＋3x. ∵AH＝AD＋DH＝20＋x， ∴2＋3x＝20＋x， 解得x＝10－， ∴BH＝2＋(10－)＝10－1≈16.3(m)． 答：立柱BH的長約為16.3 m. 9．(2016邯鄲二十五中模擬)保護視力要求人寫字時眼睛和筆端的距離應超過30 cm. 圖①是一位同學的坐姿，把他的眼睛B，肘關節(jié)C和筆端A的位置關系抽象成圖②的△ABC. 已知BC＝30 cm，AC＝22 cm，∠ACB＝53°，他的這種坐姿符合保護視力的要求嗎？請說明理由. (參考數(shù)據(jù)：sin53&#

7、176;≈0.8，cos53°≈0.6，tan53°≈1.3) 解：他的這種坐姿不符合保護視力的要求． 理由：過點B作BD⊥AC于點D. ∵BC＝30 cm，∠ACB＝53°， ∴sin53°＝＝≈0.8， 解得：BD＝24， cos53°＝≈0.6， 解得DC＝18, ∴AD＝AC－DC＝22－18＝4(cm)， ∴AB＝＝＝<， ∴他的這種坐姿不符合保護視力的要求． ,中考考點清單) 　銳角三角函數(shù)的概念 在Rt△ABC中，∠C＝90°，AB＝c，BC＝a，AC＝b，則∠A的

8、 正弦 sinA＝＝①____ 余弦 cosA＝＝②____ 正切 tanA＝＝③____ 　特殊角的三角函數(shù)值 三角函數(shù) 30° 45° 60° sinα ④____ cosα ⑤____ tanα ⑥____ 1 　解直角三角形 解直角三角形常用的關系： 在Rt△ABC中，∠C＝90°，則 三邊關系 ⑦__a2＋b2＝c2__ 兩銳角關系 ⑧__∠A＋∠B＝90°__ 邊角關系 sinA＝cosB＝ cosA＝sinB＝ tanA＝ 　解直角

9、三角形的應用 仰角、俯角 在視線與水平線所成的銳角中，視線在水平線上方的角叫⑨__仰角__，視線在水平線下方的角叫⑩__俯角__．如圖① 坡度(坡比)、坡角 坡面的鉛直高度h和?__水平寬度__l的比叫坡度(坡比)，用字母i表示；坡面與水平線的夾角α叫坡角．i＝tanα＝?____.如圖② 方位角 指北或指南方向線與目標方向線所成的小于90°的水平角，叫做?__方位角__，如圖③，A點位于O點的北偏東30°方向，B點位于O點的南偏東60°方向，C點位于O點的北偏西45°方向(或西北方向) 【規(guī)律總結】解直角三角形的方法： (1)解

10、直角三角形，當所求元素不在直角三角形中時，應作輔助線構造直角三角形，或尋找已知直角三角形中的邊角替代所要求的元素； (2)解實際問題的關鍵是構造幾何模型，大多數(shù)問題都需要添加適當?shù)妮o助線，將問題轉化為直角三角形中的邊角計算問題． ,中考重難點突破) 　銳角三角函數(shù)及特殊角三角函數(shù)值 【例1】(攀枝花中考)在△ABC中，如果∠A，∠B滿足|tanA－1|＋＝0，那么∠C＝________. 【解析】先根據(jù)非負性，得tanA＝1，cosB＝，求出∠A及∠B的度數(shù)，進而可得出結論．∵在△ABC中，tanA＝1，cosB＝，∴∠A＝45°，∠B＝60°

11、，∴∠C＝180°－∠A－∠B＝75°. 【答案】75° 1．在△ABC中，若＋＝0，則∠C的度數(shù)是(　D　) A．30°　　　B．45°　　　C．60°　　　D．90° 2．(2017天津中考)cos60°的值等于(　D　) A. B．1 C. D. 3．(2017日照中考)在Rt△ABC中，∠C＝90°，AB＝13，AC＝5，則sinA的值為(　B　) A. B. C. D. 4．(孝感中考)式子2cos30°－tan45°－的值是(　B　) A．

12、2－2 B．0 C．2 D．2 　解直角三角形的實際應用 【例2】(欽州中考)如圖，在電線桿CD上的C處引拉線CE，CF固定電線桿，拉線CE和地面所成的角∠CED＝60°，在離電線桿6 m的B處安置高為1.5 m的測角儀AB，在A處測得電線桿上C處的仰角為30°，求拉線CE的長．(結果保留小數(shù)點后一位，參考數(shù)據(jù)：≈1.41，≈1.73) 【解析】由題意可先過點A作AH⊥CD于點H，在Rt△ACH中，可求出CH，進而求出CD＝CH＋HD＝CH＋AB，再在Rt△CED中，求出CE的長． 【答案】解：過點A作AH⊥CD，垂足為H， 由題意，可知四邊形ABDH為

13、矩形，∠CAH＝30°， ∴AB＝DH＝1.5，BD＝AH＝6. 在Rt△ACH中，tan∠CAH＝， ∴CH＝AH·tan∠CAH＝6tan30°＝6×＝2(m)． ∵DH＝1.5，∴CD＝2＋1.5. 在Rt△CDE中，∠CED＝60°，sin∠CED＝， ∴CE＝＝4＋≈5.7(m)， ∴拉線CE的長約為5.7 m. 5．(2017蘭州中考)如圖，一個斜坡長130 m，坡頂離水平地面的距離為50 m，那么這個斜坡與水平地面夾角的正切值等于(　C　) A. B. C. D. (第5題圖) (第6題圖)

14、 6．(2016石家莊十一中二模)如圖，某公園入口處原有三級臺階，每級臺階高為18 cm，寬為30 cm，為方便殘疾人士，擬將臺階改為斜坡，設臺階的起點為A，斜坡的起始點為C，現(xiàn)設計斜坡BC的坡度i＝1∶5，則AC的長度是__210__cm. 7．(2016保定十七中二模)如圖，將45°的∠AOB按下面的方式放置在一把刻度尺上：頂點O與尺下沿的端點重合，OA與尺下沿重合，OB與尺上沿的交點B在尺上的讀數(shù)恰為2 cm.若按相同的方式將37°的∠AOC放置在該刻度尺上，則OC與尺上沿的交點C在尺上的讀數(shù)約為__2.7__cm.(結果精確到0.1 cm，參考數(shù)據(jù)：s

15、in37°≈0.60，cos37°≈0.80，tan37°≈0.75) 8．(2016邢臺中學二模)如圖，在一筆直的海岸線l上有A，B兩個觀測站，A在B的正東方向，AB＝2 km.有一艘小船在點P處，從A處測得小船在北偏西60°的方向，從B處測得小船在北偏東45°的方向． (1)求點P到海岸線l的距離； (2)小船從點P處沿射線AP的方向航行一段時間后，到達點C處．此時，從B處測得小船在北偏西15°的方向，求點C與點B之間的距離．(上述2小題的結果都保留根號) 解：(1)過點P作PD⊥AB于點D. 設PD＝x km.

16、在Rt△PBD中，∠BDP＝90°，∠PBD＝90°－45°＝45°， ∴BD＝PD＝x. 在Rt△PAD中，∠ADP＝90°， ∠PAD＝90°－60°＝30°， ∴AD＝PD＝x. ∵BD＋AD＝AB，∴x＋x＝2，x＝－1. ∴點P到海岸線l的距離為(－1)km； (2)過點B作BF⊥AC于點F. 根據(jù)題意，得∠ABC＝105°. 在Rt△ABF中，∠AFB＝90°，∠BAF＝30°， ∴BF＝AB＝1. 在△ABC中，∠C＝180°－∠BAC－∠ABC＝45°.在Rt△BCF中，∠BFC＝90°，∠C＝45°， ∴BC＝BF＝， ∴點C與點B之間的距離為 km.