《【冀教版】中考數(shù)學(xué)：知識(shí)清單梳理 第20講特殊的平行四邊形》由會(huì)員分享，可在線閱讀，更多相關(guān)《【冀教版】中考數(shù)學(xué)：知識(shí)清單梳理 第20講特殊的平行四邊形（2頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。
1、▼▼▼2019屆數(shù)學(xué)中考復(fù)習(xí)資料▼▼▼
第20講 特殊的平行四邊形
一、 知識(shí)清單梳理
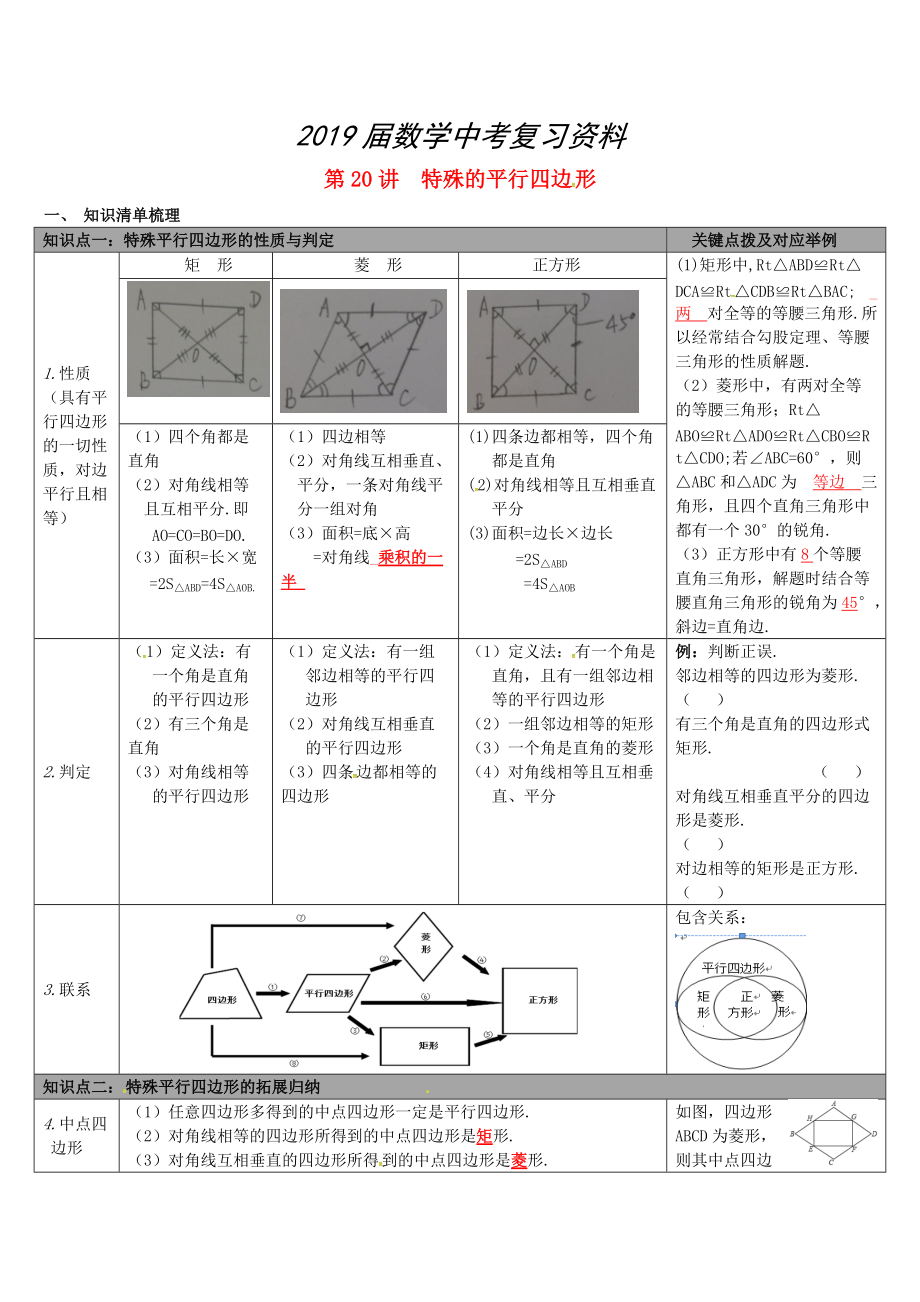
知識(shí)點(diǎn)一：特殊平行四邊形的性質(zhì)與判定
關(guān)鍵點(diǎn)撥及對(duì)應(yīng)舉例
1.性質(zhì)
（具有平行四邊形的一切性質(zhì)，對(duì)邊平行且相等）
矩 形
菱 形
正方形
(1)矩形中,Rt△ABD≌Rt△DCA≌Rt△CDB≌Rt△BAC; _兩 對(duì)全等的等腰三角形.所以經(jīng)常結(jié)合勾股定理、等腰三角形的性質(zhì)解題.
（2）菱形中，有兩對(duì)全等的等腰三角形；Rt△ABO≌Rt△ADO≌Rt△CBO≌Rt△CDO;若∠ABC=60，則△ABC和△ADC為 等邊 三角形，且四個(gè)直角三角形中都有一個(gè)30的
2、銳角.
（3）正方形中有8個(gè)等腰直角三角形，解題時(shí)結(jié)合等腰直角三角形的銳角為45，斜邊=直角邊.
（1）四個(gè)角都是直角
（2）對(duì)角線相等且互相平分.即
AO=CO=BO=DO.
（3）面積=長(zhǎng)寬
=2S△ABD=4S△AOB.
（1）四邊相等
（2）對(duì)角線互相垂直、平分，一條對(duì)角線平分一組對(duì)角
（3）面積=底高
=對(duì)角線_乘積的一半
(1)四條邊都相等，四個(gè)角都是直角
(2)對(duì)角線相等且互相垂直平分
(3)面積=邊長(zhǎng)邊長(zhǎng)
=2S△ABD
=4S△AOB
2.判定
（1）定義法：有一個(gè)角是直角的平行四邊形
（2）有三個(gè)角是直角
（3）對(duì)角線相等
3、的平行四邊形
（1）定義法：有一組鄰邊相等的平行四邊形
（2）對(duì)角線互相垂直的平行四邊形
（3）四條邊都相等的四邊形
（1）定義法：有一個(gè)角是直角，且有一組鄰邊相等的平行四邊形
（2）一組鄰邊相等的矩形
（3）一個(gè)角是直角的菱形
（4）對(duì)角線相等且互相垂直、平分
例：判斷正誤.
鄰邊相等的四邊形為菱形.（ ）
有三個(gè)角是直角的四邊形式矩形.
（ ）
對(duì)角線互相垂直平分的四邊形是菱形. （ ）
對(duì)邊相等的矩形是正方形.（ ）
3.聯(lián)系
包含關(guān)系：
4、
知識(shí)點(diǎn)二：特殊平行四邊形的拓展歸納
4.中點(diǎn)四邊形
（1）任意四邊形多得到的中點(diǎn)四邊形一定是平行四邊形.
（2）對(duì)角線相等的四邊形所得到的中點(diǎn)四邊形是矩形.
（3）對(duì)角線互相垂直的四邊形所得到的中點(diǎn)四邊形是菱形.
（4）對(duì)角線互相垂直且相等的四邊形所得到的中點(diǎn)四邊形是正方形.
如圖，四邊形ABCD為菱形，則其中點(diǎn)四邊形EFGD的形狀是矩形.
5.特殊四邊形中的解題模型
（1）矩形：如圖①，E為AD上任意一點(diǎn)，EF過矩形中心O，則△AOE≌△COF,S1=S2.
（2）正方形:如圖②，若EF⊥MN，則EF=MN;如圖③，P為AD邊上任意一點(diǎn)，則PE+PF=AO. （變式：如圖④，四邊形ABCD為矩形，則PE+PF的求法利用面積法，需連接PO.）
圖① 圖② 圖③ 圖④
【冀教版】中考數(shù)學(xué)：知識(shí)清單梳理 第20講特殊的平行四邊形
