安徽省長豐縣高中數(shù)學 第一章 統(tǒng)計案例 1.1 回歸分析的基本思想及其初步應用1教案 新人教A版選修12

《安徽省長豐縣高中數(shù)學 第一章 統(tǒng)計案例 1.1 回歸分析的基本思想及其初步應用1教案 新人教A版選修12》由會員分享，可在線閱讀，更多相關《安徽省長豐縣高中數(shù)學 第一章 統(tǒng)計案例 1.1 回歸分析的基本思想及其初步應用1教案 新人教A版選修12（3頁珍藏版）》請在裝配圖網上搜索。

1、 1.1回歸分析的基本思想及其初步應用(1) 項目 內容 課題 1.1回歸分析的基本思想及其初步應用(1) 修改與創(chuàng)新 教學目標 1、 通過典型案例的探究，進一步了解回歸分析的基本思想、方法 2、 鞏固掌握回歸分析的基本思想、方法初步應用. 3、 掌握函數(shù)模型擬合效果優(yōu)劣判斷方法。 教學重、 難點 重點：了解線性回歸模型與函數(shù)模型的差異 難點：了解判斷刻畫模型擬合效果的方法－相關指數(shù)和殘差分析. 教學準備 直尺 教學過程 一、復習準備： 1. 提問：“名師出高徒”這句彥語的意思是什么？有名氣的老師就一定能教出厲害的學生嗎？這兩者之間是否有關

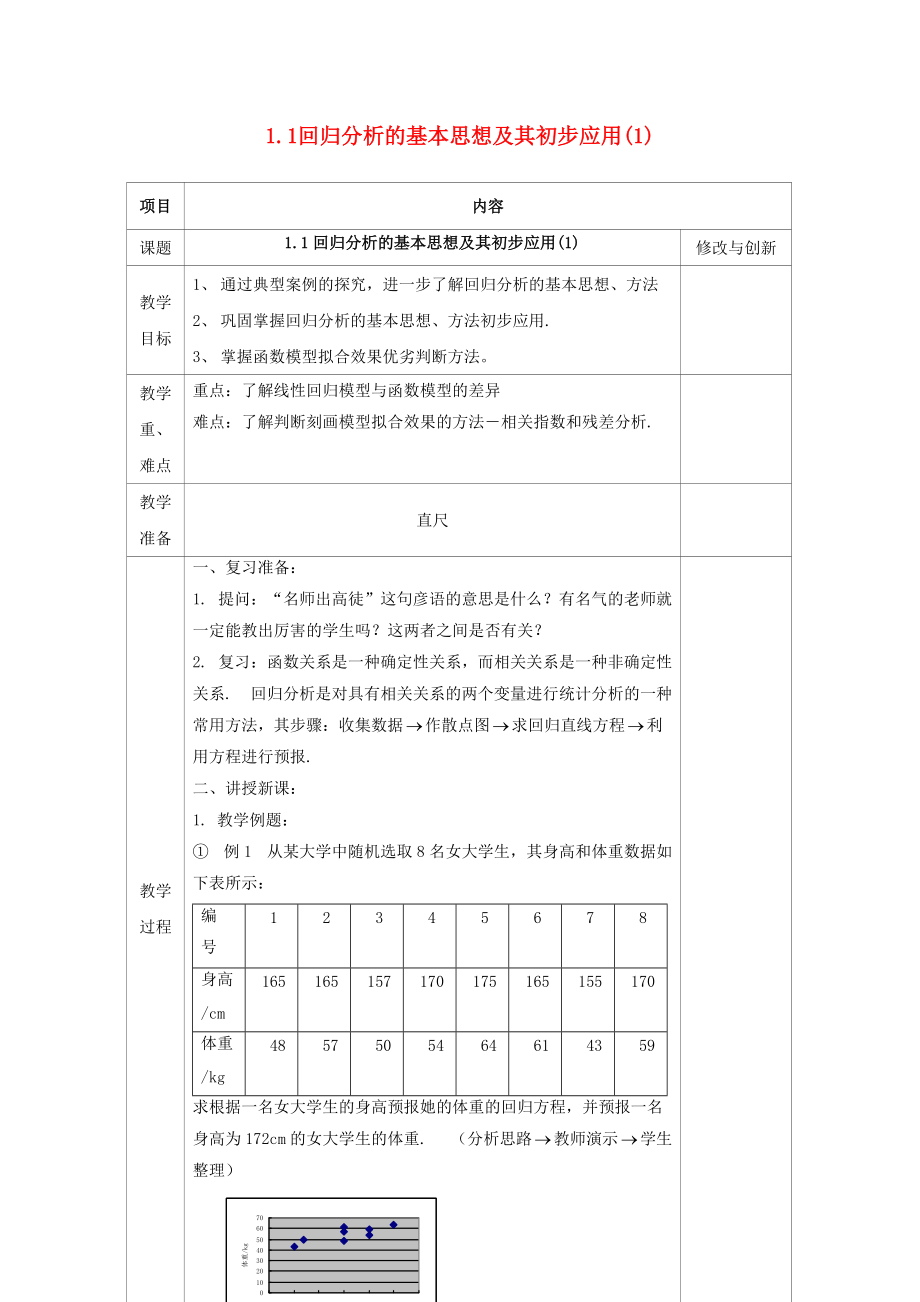
2、？ 2. 復習：函數(shù)關系是一種確定性關系，而相關關系是一種非確定性關系. 回歸分析是對具有相關關系的兩個變量進行統(tǒng)計分析的一種常用方法，其步驟：收集數(shù)據作散點圖求回歸直線方程利用方程進行預報. 二、講授新課： 1. 教學例題： ① 例1 從某大學中隨機選取8名女大學生，其身高和體重數(shù)據如下表所示： 編　號 　1 　2 　3 　4 　5 　6 　7 　8 身高/cm 165 165 157 170 175 165 155 170 體重/kg 48 57 50 54 64 61 43 59

3、求根據一名女大學生的身高預報她的體重的回歸方程，并預報一名身高為172cm的女大學生的體重. （分析思路教師演示學生整理） 　第一步：作散點圖 第二步：求回歸方程 第三步：代值計算 ② 提問：身高為172cm的女大學生的體重一定是60.316kg嗎？ 不一定，但一般可以認為她的體重在60.316kg左右. ③ 解釋線性回歸模型與一次函數(shù)的不同 事實上，觀察上述散點圖，我們可以發(fā)現(xiàn)女大學生的體重和身高之間的關系并不能用一次函數(shù)來嚴格刻畫（因為所有的樣本點不共線，所以線性模型只能近似地刻畫身高和體重的關系）. 在數(shù)據表中身高為165cm的3名女大學生的體重分別為

4、48kg、57kg和61kg，如果能用一次函數(shù)來描述體重與身高的關系，那么身高為165cm的3名女在學生的體重應相同. 這就說明體重不僅受身高的影響還受其他因素的影響，把這種影響的結果（即殘差變量或隨機變量）引入到線性函數(shù)模型中，得到線性回歸模型，其中殘差變量中包含體重不能由身高的線性函數(shù)解釋的所有部分. 當殘差變量恒等于0時，線性回歸模型就變成一次函數(shù)模型. 因此，一次函數(shù)模型是線性回歸模型的特殊形式，線性回歸模型是一次函數(shù)模型的一般形式. 2. 相關系數(shù)：相關系數(shù)的絕對值越接近于1，兩個變量的線性相關關系越強，它們的散點圖越接近一條直線，這時用線性回歸模型擬合這組數(shù)據就越好，此時建立的

5、線性回歸模型是有意義. 3. 小結：求線性回歸方程的步驟、線性回歸模型與一次函數(shù)的不同. 板書設計 1.1回歸分析的基本思想及其初步應用(1) 1.相關關系 2.線性回歸方程 3. 其中， 4.殘差 課后反思 本節(jié)內容是對必修三的第二章線性回歸的復習與深化。教學時，先讓學生復習線性回歸的相關知識。 相關關系是非確定關系，自然會聯(lián)想到，利用回歸方程進行預報，其準確性如何？如何衡量擬合的效果？進而引進課題。畫出圖殘差后，讓學生自己分析如何利用殘差圖判斷擬合的效果。 主 我國經濟發(fā)展進入新常態(tài)，需要轉變經濟發(fā)展方式，改變粗放式增長模式，不斷優(yōu)化經濟結構，實現(xiàn)經濟健康可持續(xù)發(fā)展進區(qū)域協(xié)調發(fā)展，推進新型城鎮(zhèn)化，推動城鄉(xiāng)發(fā)展一體化因：我國經濟發(fā)展還面臨區(qū)域發(fā)展不平衡、城鎮(zhèn)化水平不高、城鄉(xiāng)發(fā)展不平衡不協(xié)調等現(xiàn)實挑戰(zhàn)。