《【優(yōu)化設(shè)計(jì)】(福建專版)2015中考數(shù)學(xué)總復(fù)習(xí) 第12課時(shí) 二次函數(shù)模擬預(yù)測》由會(huì)員分享����,可在線閱讀,更多相關(guān)《【優(yōu)化設(shè)計(jì)】(福建專版)2015中考數(shù)學(xué)總復(fù)習(xí) 第12課時(shí) 二次函數(shù)模擬預(yù)測(3頁珍藏版)》請?jiān)谘b配圖網(wǎng)上搜索����。
1、
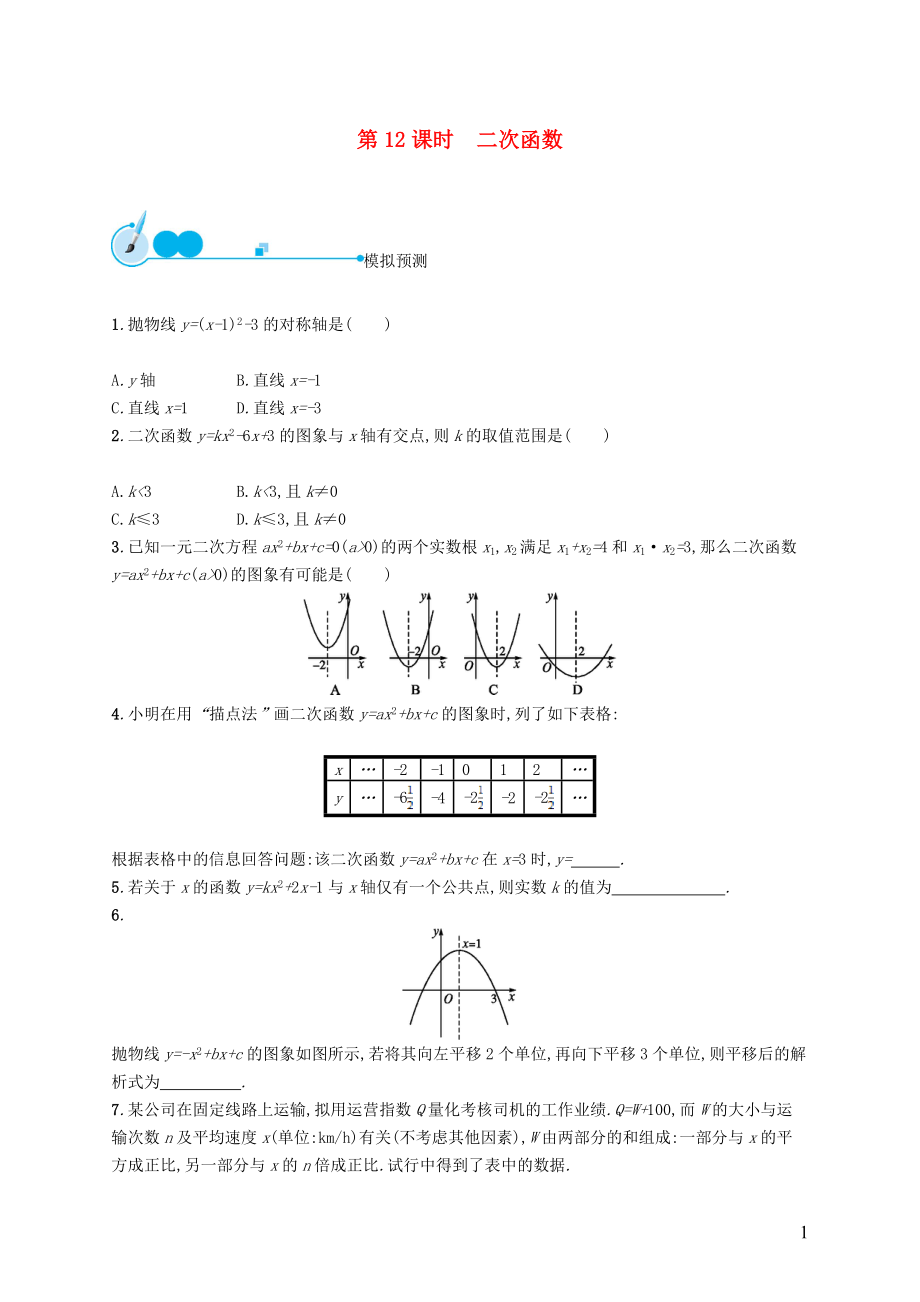
第12課時(shí) 二次函數(shù)
模擬預(yù)測
1.拋物線y=(x-1)2-3的對稱軸是( )
A.y軸 B.直線x=-1
C.直線x=1 D.直線x=-3
2.二次函數(shù)y=kx2-6x+3的圖象與x軸有交點(diǎn),則k的取值范圍是( )
A.k<3 B.k<3,且k≠0
C.k≤3 D.k≤3,且k≠0
3.已知一元二次方程ax2+bx+c=0(a>0)的兩個(gè)實(shí)數(shù)根x1,x2滿足x1+x2=4和x1·x2=3,那么二次函數(shù)y=ax2+bx+c(a>0)的圖象有可能是( )
4.小明在用“描點(diǎn)法”畫二次函
2�����、數(shù)y=ax2+bx+c的圖象時(shí),列了如下表格:
x
…
-2
-1
0
1
2
…
y
…
-6
-4
-2
-2
-2
…
根據(jù)表格中的信息回答問題:該二次函數(shù)y=ax2+bx+c在x=3時(shí),y= .?
5.若關(guān)于x的函數(shù)y=kx2+2x-1與x軸僅有一個(gè)公共點(diǎn),則實(shí)數(shù)k的值為 .?
6.
拋物線y=-x2+bx+c的圖象如圖所示,若將其向左平移2個(gè)單位,再向下平移3個(gè)單位,則平移后的解析式為 .?
7.某公司在固定線路上運(yùn)輸,擬用運(yùn)營指數(shù)Q量化考核司機(jī)的工作業(yè)績.Q=W+100,而W的大小與運(yùn)輸次數(shù)n及平均速度x
3����、(單位:km/h)有關(guān)(不考慮其他因素),W由兩部分的和組成:一部分與x的平方成正比,另一部分與x的n倍成正比.試行中得到了表中的數(shù)據(jù).
次數(shù)n
2
1
速度x
40
60
指數(shù)Q
420
100
(1)用含x和n的式子表示Q;
(2)當(dāng)x=70,Q=450時(shí),求n的值;
(3)若n=3,要使Q最大,確定x的值;
(4)設(shè)n=2,x=40,能否在n增加m%(m>0)同時(shí)x減少m%的情況下,而Q的值仍為420?若能,求出m的值;若不能,請說明理由.
參考公式:拋物線y=ax2+bx+c(a≠0)的頂點(diǎn)坐標(biāo)是.
答案
4、1.C 2.D
3.C ∵x1+x2=4,
∴-=4.
∴二次函數(shù)的對稱軸為x=-=2.
∵x1·x2=3,
∴=3.
當(dāng)a>0時(shí),c>0,∴二次函數(shù)圖象交于y軸的正半軸.
4.-4
5.k=0或k=-1
6.y=-x2-2x 由題中圖象可知,對稱軸x=1,
所以-=1,即b=2.把點(diǎn)(3,0)代入y=-x2+2x+c,得c=3.
故原圖象的解析式為y=-x2+2x+3,即y=-(x-1)2+4,然后向左平移2個(gè)單位,再向下平移3個(gè)單位,得y=-(x-1+2)2+4-3,即y=-x2-2x.
7.解:(1)設(shè)W=k1x2+k2nx,則Q=k1x2+k2nx+100.
由表中數(shù)據(jù),得
解得
因此Q=-x2+6nx+100.
(2)由題意,得450=-×702+6×70n+100.
解得n=2.
(3)當(dāng)n=3時(shí),則Q=-x2+18x+100.
由a=-<0可知,要使Q最大,
則x=-=90.
(4)由題意,得
420=-[40(1-m%)]2+6×2(1+m%)×40(1-m%)+100.
即2(m%)2-m%=0,
解得m%=,或m%=0(舍去).故m=50.
3
 【優(yōu)化設(shè)計(jì)】(福建專版)2015中考數(shù)學(xué)總復(fù)習(xí) 第12課時(shí) 二次函數(shù)模擬預(yù)測
【優(yōu)化設(shè)計(jì)】(福建專版)2015中考數(shù)學(xué)總復(fù)習(xí) 第12課時(shí) 二次函數(shù)模擬預(yù)測