【優(yōu)化設計】（福建專版）2015中考數(shù)學總復習 第19課時 圓的有關性質模擬預測

《【優(yōu)化設計】（福建專版）2015中考數(shù)學總復習 第19課時 圓的有關性質模擬預測》由會員分享，可在線閱讀，更多相關《【優(yōu)化設計】（福建專版）2015中考數(shù)學總復習 第19課時 圓的有關性質模擬預測（4頁珍藏版）》請在裝配圖網上搜索。

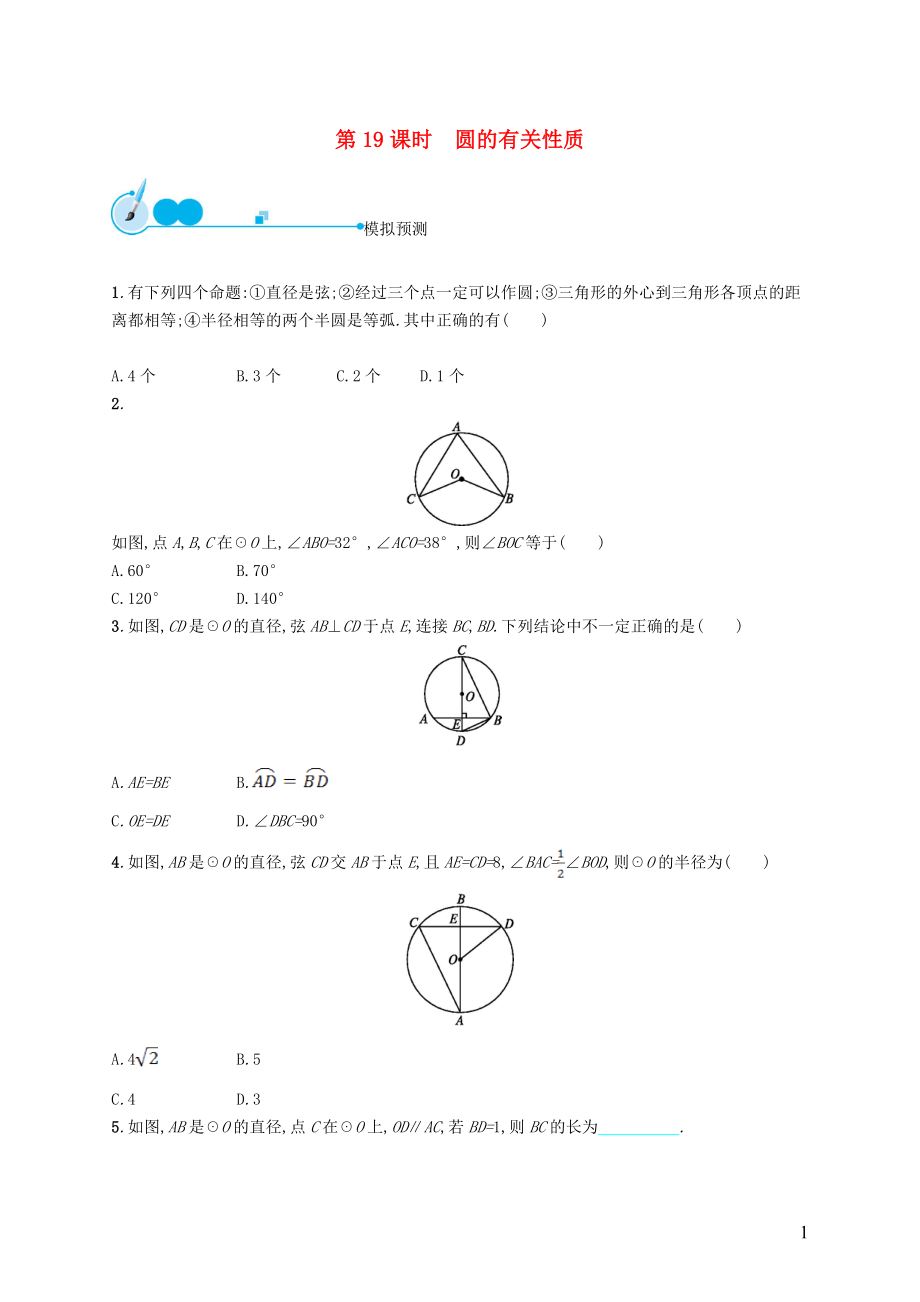
1、 第19課時　圓的有關性質 模擬預測 1.有下列四個命題:①直徑是弦;②經過三個點一定可以作圓;③三角形的外心到三角形各頂點的距離都相等;④半徑相等的兩個半圓是等弧.其中正確的有(　　) 　　　　　　　　　　　　　　　　 A.4個 B.3個 C.2個 D.1個 2. 如圖,點A,B,C在☉O上,∠ABO=32°,∠ACO=38°,則∠BOC等于(　　) A.60° B.70° C.120° D.140° 3.如圖,CD是☉O的直徑,弦AB⊥CD于點E,連接BC,BD.下列結論中不一定正確的是(　　) A.AE=BE B. C.OE=DE D.∠DBC=90°

2、 4.如圖,AB是☉O的直徑,弦CD交AB于點E,且AE=CD=8,∠BAC=∠BOD,則☉O的半徑為(　　) A.4 B.5 C.4 D.3 5.如圖,AB是☉O的直徑,點C在☉O上,OD∥AC,若BD=1,則BC的長為　　　　　.? 6.如圖,△ABC是☉O的內接三角形,點D是的中點,已知∠AOB=98°,∠COB=120°.則∠ABD的度數(shù)是　　　　　.? 7.如圖,水平放置的圓柱形排水管道的截面直徑是1 m,其中水面的寬AB為0.8 m,則排水管內水的深度為　　　　m.? 8.如圖,△ABC是☉O的內接三角形,AD⊥BC于D點,且AC=5,DC=3,A

3、B=4,則☉O的直徑等于　　　　.? 9.如圖,AB是☉O的直徑,弦CD⊥AB于點E,點P在☉O上,∠1=∠C. (1)求證:CB∥PD; (2)若BC=3,sin P=,求☉O的直徑. 答案 1.B 2.D　過點A作☉O的直徑,交☉O于點D. 在△OAB中,∵OA=OB, ∴∠BOD=∠OBA+∠OAB=2×32°=64°. 同理可得,∠COD=∠OCA+∠OAC=2×38°=76°, ∴∠BOC=∠BOD+∠COD=140°.故選D. 3.C 4.B　∵∠BAC=∠BOD, ∴,∴AB⊥CD. ∵AE=CD=8,∴DE=CD=4.

4、 設OD=r,則OE=AE-r=8-r.在Rt△ODE中,OD=r,DE=4,OE=8-r, ∵OD2=DE2+OE2,即r2=42+(8-r)2,解得r=5.故選B. 5.2　6.101° 7. 0.2　過點O作OD⊥AB,垂足為點C,交☉O于點D,連接OA,則AC=AB=0.4 m,OA=×1=0.5(m). 在Rt△OAC中,由勾股定理,得OC==0.3(m). ∴排水管內水的深度為CD=OD-OC=0.5-0.3=0.2(m). 8. 5　連接AO,并延長交☉O于點E,連接BE.(如圖) ∵AE為☉O的直徑, ∴∠ABE=90°. ∵AD⊥BC, ∴∠ABE=∠ADC. 又∵∠AEB=∠ACD, ∴△ABE∽△ADC. ∴. ∵在Rt△ADC中,AC=5,DC=3, ∴AD=4. ∴AE=5. 9. 解：(1)證明：∵∠D=∠1,∠1=∠C, ∴∠D=∠C. ∴CB∥PD. (2)解:連接AC,如圖. ∵AB是☉O的直徑,弦CD⊥AB于點E, ∴, ∴∠P=∠A. ∴sin A=sin P=. 又因為AB為☉O的直徑, ∴∠ACB=90°. ∴sin A=. ∵BC=3, ∴AB=5, 即☉O的直徑為5. 4