《【優(yōu)化設(shè)計(jì)】（福建專版）2015中考數(shù)學(xué)總復(fù)習(xí) 第24課時(shí) 圖形的軸對(duì)稱與中心對(duì)稱模擬預(yù)測》由會(huì)員分享，可在線閱讀，更多相關(guān)《【優(yōu)化設(shè)計(jì)】（福建專版）2015中考數(shù)學(xué)總復(fù)習(xí) 第24課時(shí) 圖形的軸對(duì)稱與中心對(duì)稱模擬預(yù)測（3頁珍藏版）》請?jiān)谘b配圖網(wǎng)上搜索。
1、
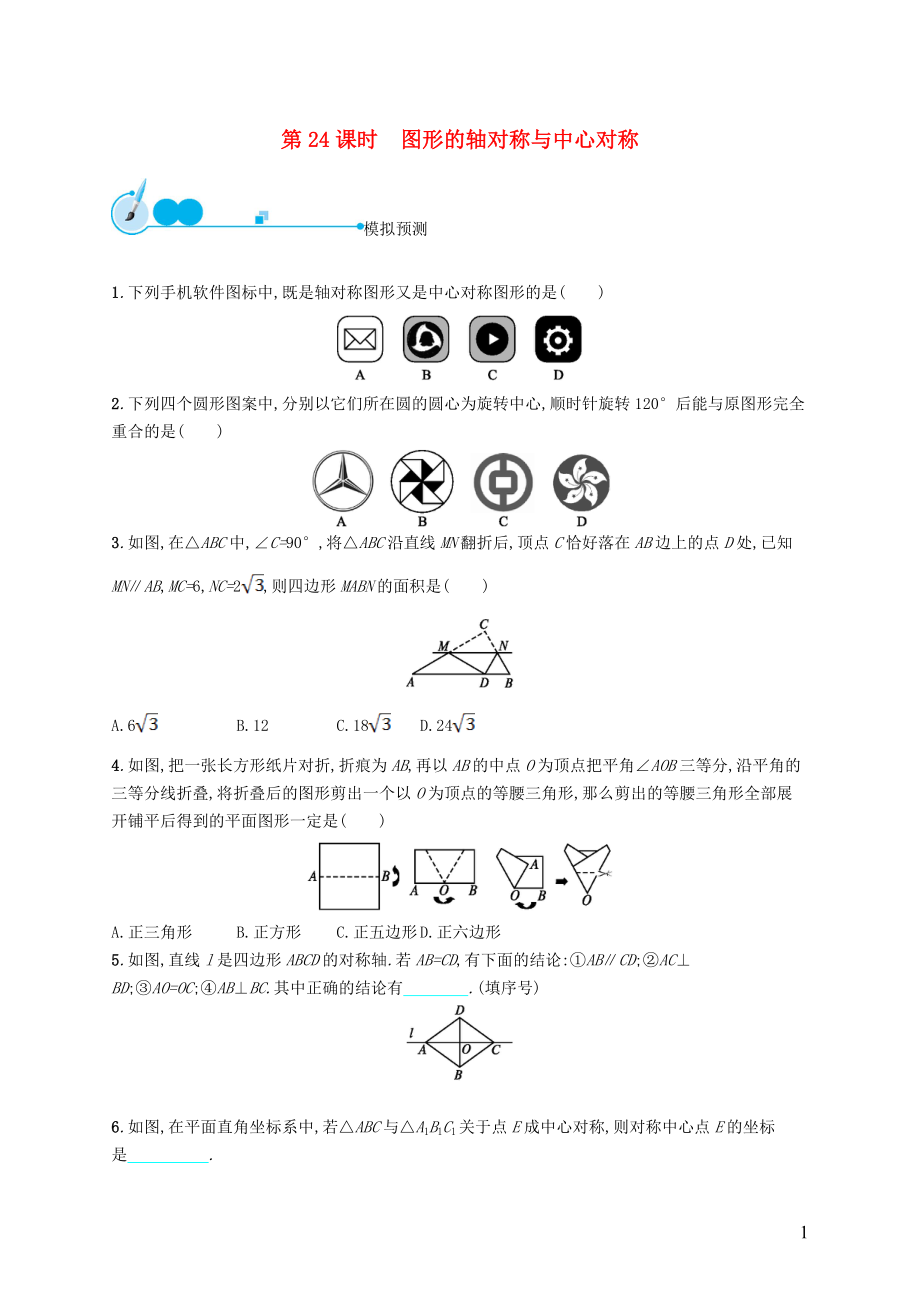
第24課時(shí) 圖形的軸對(duì)稱與中心對(duì)稱
模擬預(yù)測
1.下列手機(jī)軟件圖標(biāo)中,既是軸對(duì)稱圖形又是中心對(duì)稱圖形的是( )
2.下列四個(gè)圓形圖案中,分別以它們所在圓的圓心為旋轉(zhuǎn)中心,順時(shí)針旋轉(zhuǎn)120°后能與原圖形完全重合的是( )
3.如圖,在△ABC中,∠C=90°,將△ABC沿直線MN翻折后,頂點(diǎn)C恰好落在AB邊上的點(diǎn)D處,已知MN∥AB,MC=6,NC=2,則四邊形MABN的面積是( )
A.6 B.12 C.18 D.24
4.如圖,把一張長方形紙片對(duì)折,折痕為AB,再以AB的中點(diǎn)O為頂點(diǎn)把平角∠AOB三等分,沿平角的三等分線折疊,將折疊后的圖形剪出一個(gè)以O(shè)為
2、頂點(diǎn)的等腰三角形,那么剪出的等腰三角形全部展開鋪平后得到的平面圖形一定是( )
A.正三角形 B.正方形 C.正五邊形 D.正六邊形
5.如圖,直線l是四邊形ABCD的對(duì)稱軸.若AB=CD,有下面的結(jié)論:①AB∥CD;②AC⊥BD;③AO=OC;④AB⊥BC.其中正確的結(jié)論有 .(填序號(hào))?
6.如圖,在平面直角坐標(biāo)系中,若△ABC與△A1B1C1關(guān)于點(diǎn)E成中心對(duì)稱,則對(duì)稱中心點(diǎn)E的坐標(biāo)是 .?
7.在Rt△ABC中,∠BAC=90°,AB=3,M為邊BC上的點(diǎn),連接AM(如圖所示).如果△ABM沿直線AM翻折后,點(diǎn)B恰好落在邊AC的中點(diǎn)處,那么點(diǎn)M
3、到AC的距離是 .?
8.△ABC在平面直角坐標(biāo)系中的位置如圖所示.
(1)作出△ABC關(guān)于y軸對(duì)稱的△A1B1C1,并寫出△A1B1C1各頂點(diǎn)的坐標(biāo);
(2)將△ABC向右平移6個(gè)單位,作出平移后的△A2B2C2,并寫出△A2B2C2各頂點(diǎn)的坐標(biāo);
(3)觀察△A1B1C1與△A2B2C2,它們是否關(guān)于某直線對(duì)稱?若是,請?jiān)趫D上畫出這條對(duì)稱軸.
答案
1.D 2.A
3.C S△CMN=CM·CN=6.因?yàn)镸N∥AB,△ABC沿直線MN翻折后,頂點(diǎn)C恰好落在AB邊上的點(diǎn)D處,可知MN是△ABC的中位線,所以S△ABC=4S△CMN=24,故四邊形MABN
4、的面積=△ABC的面積-△CMN的面積=18.
4.D 根據(jù)第一次對(duì)折以及三等分平角可知將360°進(jìn)行6等分,即多邊形的中心角為60°,由最后的剪切可知所得圖形符合正六邊形特征.故選D.
5.①②③
6.(3,-1)
7.2 如圖,過點(diǎn)M作MN⊥AC于N,
由折疊性質(zhì)可知,∠BAM=∠CAM=45°.
∵點(diǎn)B恰好落在邊AC的中點(diǎn)處,
∴AC=2AB=6.
∵∠ANM=90°,∴∠CAM=∠AMN=45°.
∴MN=AN.
由Rt△CNM∽R(shí)t△CAB,得,
∴.∴MN=2.
8.解:(1)△A1B1C1如圖,A1(0,4),B1(2,2),C1(1,1);(2)△A2B2C2如圖.A2(6,4),B2(4,2),C2(5,1);(3)△A1B1C1與△A2B2C2關(guān)于直線x=3對(duì)稱.如圖.
3
【優(yōu)化設(shè)計(jì)】（福建專版）2015中考數(shù)學(xué)總復(fù)習(xí) 第24課時(shí) 圖形的軸對(duì)稱與中心對(duì)稱模擬預(yù)測
