《人教版九下數(shù)學(xué) 第二十八章 專題類型二 回歸教材（二） 圓與三角函數(shù)（2） 利用“直徑”構(gòu)造直角三角形》由會(huì)員分享，可在線閱讀，更多相關(guān)《人教版九下數(shù)學(xué) 第二十八章 專題類型二 回歸教材（二） 圓與三角函數(shù)（2） 利用“直徑”構(gòu)造直角三角形（3頁珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。
1、
人教版九下數(shù)學(xué) 第二十八章 專題類型二 回歸教材（二） 圓與三角函數(shù)（2） 利用“直徑”構(gòu)造直角三角形
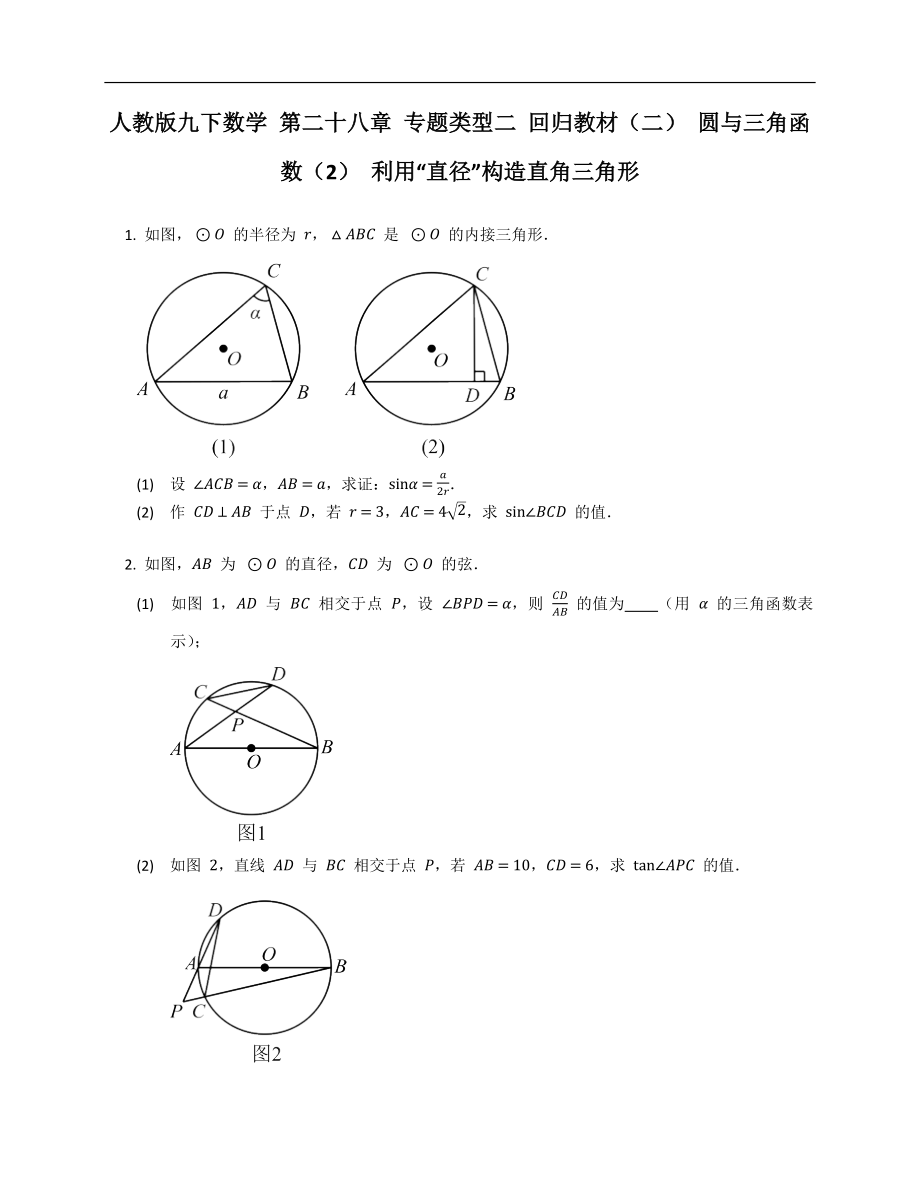
1. 如圖，⊙O 的半徑為 r，△ABC 是 ⊙O 的內(nèi)接三角形．
(1) 設(shè) ∠ACB=α，AB=a，求證：sinα=a2r．
(2) 作 CD⊥AB 于點(diǎn) D，若 r=3，AC=42，求 sin∠BCD 的值．
2. 如圖，AB 為 ⊙O 的直徑，CD 為 ⊙O 的弦．
(1) 如圖 1，AD 與 BC 相交于點(diǎn) P，設(shè) ∠BPD=α，則 CDAB 的值為 （用 α 的三角函數(shù)表示）；
(2) 如圖 2，直線 AD 與 BC 相交于點(diǎn) P
2、，若 AB=10，CD=6，求 tan∠APC 的值．
3. 如圖，△ABC 內(nèi)接于 ⊙O，AB=AC，連接 AO．
(1) 求證：AO⊥BC；
(2) CO 的延長線交 AB 于點(diǎn) D，若 tan∠BAC=34，求 ADDB 的值．
答案
1. 【答案】
(1) 作直徑 AC1，連接 BC1，
則 ∠ABC1=90°，∠AC1B=∠ACB=α，
∴ 在 Rt△ABC1 中，sinα=ABAC1=a2r；
(2) 作直徑 CB1 連接 AB1，
則 ∠B1=∠B，∠CAB1=90°=∠CDB，
∴∠BCD=∠ACB1，AB1=CB12-AC2=
3、2，
∴sin∠BCD=sin∠ACB1=AB1CB1=13．
2. 【答案】
(1) cosα
(2) 連接 BD，同理易證 cos∠BPD=CDAB=610=35，
∴ 可設(shè) PD=3a，則 PB=5a，BD=4a，
∴ 在 Rt△PBD 中，tan∠APC=BDPD=43．
【解析】
(1) 連接 BD，則 ∠ADB=90°，
易證 △PCD∽△PAB，
∴CDAB=PDPB=cos∠BPD=cosα．
3. 【答案】
(1) 略．
(2) 延長 CD 交 ⊙O 于點(diǎn) E，連接 BE，則 ∠EBC=90°，∠E=∠BAC，
∴tan∠E=tan∠BAC=BCBE=34，
∴ 可設(shè) BC=6a，則 BE=8a，
∴EC=BC2+BE2=10a，AO=12EC=5a，由（1）知 AO∥EB，
∴ 易證 △AOD∽△BED，
∴ADDB=AOBE=5a8a=58．
人教版九下數(shù)學(xué) 第二十八章 專題類型二 回歸教材（二） 圓與三角函數(shù)（2） 利用“直徑”構(gòu)造直角三角形
