《2021八年級數(shù)學(xué)下冊 第二章 四邊形（一）復(fù)習(xí)教案 （新版）湘教版》由會員分享，可在線閱讀，更多相關(guān)《2021八年級數(shù)學(xué)下冊 第二章 四邊形（一）復(fù)習(xí)教案 （新版）湘教版（3頁珍藏版）》請?jiān)谘b配圖網(wǎng)上搜索。
1、
四邊形復(fù)習(xí)（一）
課題
第二章 四邊形復(fù)習(xí)（一）
本課（章節(jié)）需16課時(shí) ，本節(jié)課為第15課時(shí)，為本學(xué)期總第25課時(shí)
教學(xué)目標(biāo)
知識與技能：理解四邊形、平行四邊形、矩形、菱形、正方形的有關(guān)概念；掌握平行四邊形、矩形、菱形、正方形的有關(guān)性質(zhì)和常用判別方法。
過程與方法：經(jīng)歷探究四邊形、平行四邊形、矩形、菱形、正方形之間的聯(lián)系與區(qū)別的過程，類比掌握平行四邊形、矩形、菱形、正方形的性質(zhì)與常用的判別方法。
情感態(tài)度與價(jià)值觀：在回顧與思考的過程中，讓學(xué)生進(jìn)一步領(lǐng)會特殊與一般的關(guān)系，逐漸理解類比、轉(zhuǎn)化等一些重要的數(shù)學(xué)思想。
重點(diǎn)
建立知識結(jié)構(gòu)，掌握特殊四邊形之間的聯(lián)系與區(qū)別
難點(diǎn)
2、
靈活應(yīng)用所學(xué)知識解決有關(guān)問題
教學(xué)方法
課型
教具
教學(xué)過程：
一、合作復(fù)習(xí)、知識梳理
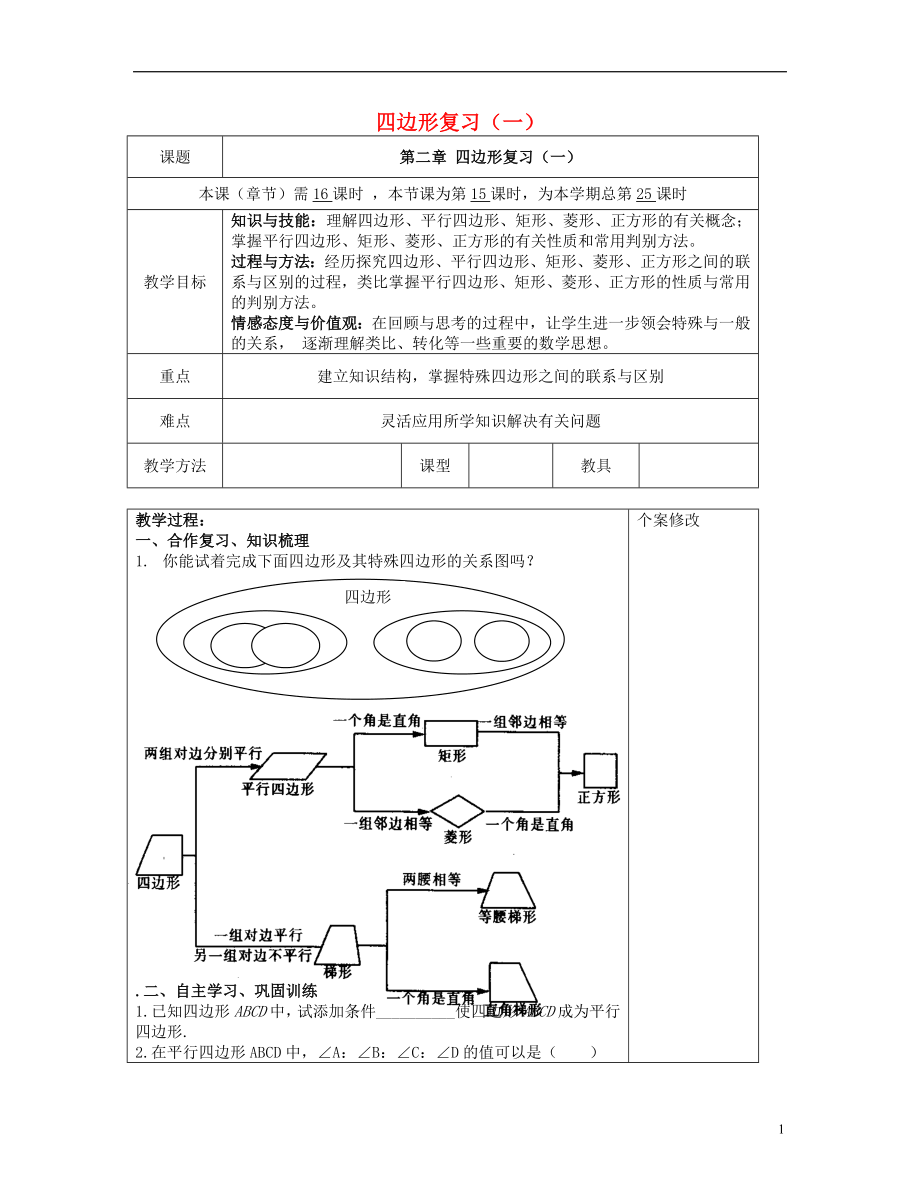
1. 你能試著完成下面四邊形及其特殊四邊形的關(guān)系圖嗎？
四邊形
.二、自主學(xué)習(xí)、鞏固訓(xùn)練
1.已知四邊形ABCD中，試添加條件__________使四邊形ABCD成為平行四邊形.
2.在平行四邊形ABCD中，∠A：∠B：∠C：∠D的值可以是（ ?。?
A．1：2：3：4 B．1：2：2：1 C．2：2：1：1 D．2：1：2：1
3.平行四邊形ABCD的周長為60cm，對角線交于O
3、，△AOB的周長比△BOC的周長大8cm，則AB、BC的長分別是_________．
4.平行四邊形ABCD中，AC，BD是兩條對角線，如果添加一個條件，即可推出平行四邊形ABCD是矩形，那么這個條件是（ ）
A．AB=BC B．AC=BD C．AC⊥BD D．AB⊥BD
5.矩形的兩條對角線的夾角為60°，一對角線與短邊的和為15，對角線長是____，面積等于____．
6.已知菱形兩鄰角的比是1：2，周長是40cm，則較短對角線長是______.
7.菱形的兩條對角線長分別為16cm，12cm，那么這個菱形的高是______．
8.如圖1，
4、已知P是正方形ABCD對角線BD上一點(diǎn)，且BP = BC，則∠ACP度數(shù)是 ．
9.如圖2所示，菱形中，對角線相交于點(diǎn)，若再補(bǔ)充一個條件能使菱形成為正方形，則這個條件是_________（填一個條件即可）
三、綜合運(yùn)用
例1、如圖4，矩形ABCD的對角線AC、BD交于點(diǎn)O，過點(diǎn)D作DP∥OC，且 DP=OC，連結(jié)CP，試判斷四邊形CODP的形狀．并證明。
變式一：如果題目中的矩形變?yōu)榱庑?，結(jié)論應(yīng)變?yōu)槭裁矗?
變式二：如果題目中的矩形變?yōu)檎叫?，結(jié)論又應(yīng)變?yōu)槭裁矗?
例2：如圖5，正方形ABCD的邊CD在正方形ECGF的邊CE上，連接BE.DG.
5、觀察猜想BE與DG之間的關(guān)系，并證明你的結(jié)論；
1.將兩塊能完全重合的兩張等腰直角三角形紙片拼成下列圖形：①平行四邊形（不包括菱形、矩形、正方形）②矩形③正方形④等邊三角形⑤等腰直角三角形( ).
A.①③⑤ B.②③⑤ C.①②③ D.①③④⑤
2.如圖6，EF為正方形紙片ABCD的對折線，將∠A沿DK折疊，使它的頂點(diǎn)A落在EF上的G點(diǎn)，則∠DKG的度數(shù)是________．
3.如圖7，在直角ΔABC中，直角∠ABC的平分線交AC于點(diǎn)D，DE⊥AB于點(diǎn)E，DF⊥BC于點(diǎn)F，那么四邊形EBFD是正方形嗎？為什么？
四、小結(jié)：
在下列圖表中用文字或符號語言寫出判定某種特殊四邊形的各種條件：
五、 作業(yè)
教材 P77——P78 復(fù)習(xí)題 3、4、7、8、9、10、11
個案修改
3
2021八年級數(shù)學(xué)下冊 第二章 四邊形（一）復(fù)習(xí)教案 （新版）湘教版
