高中物理 第二章 圓周運(yùn)動(dòng) 第2節(jié) 向心力素材 粵教版必修2（通用）

《高中物理 第二章 圓周運(yùn)動(dòng) 第2節(jié) 向心力素材 粵教版必修2（通用）》由會(huì)員分享，可在線閱讀，更多相關(guān)《高中物理 第二章 圓周運(yùn)動(dòng) 第2節(jié) 向心力素材 粵教版必修2（通用）（3頁珍藏版）》請?jiān)谘b配圖網(wǎng)上搜索。

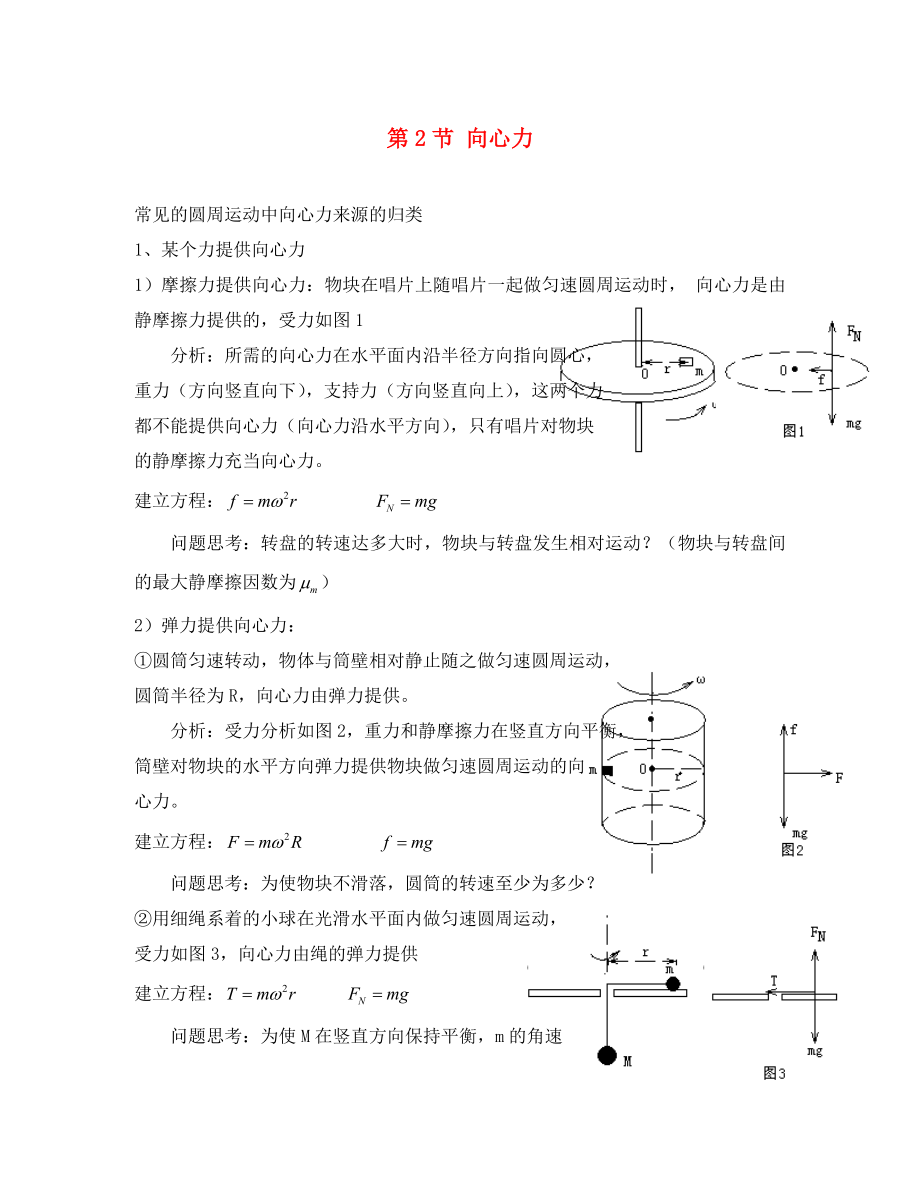
1、第2節(jié) 向心力 常見的圓周運(yùn)動(dòng)中向心力來源的歸類 1、某個(gè)力提供向心力 1）摩擦力提供向心力：物塊在唱片上隨唱片一起做勻速圓周運(yùn)動(dòng)時(shí)， 向心力是由靜摩擦力提供的，受力如圖1 分析：所需的向心力在水平面內(nèi)沿半徑方向指向圓心， 重力（方向豎直向下），支持力（方向豎直向上），這兩個(gè)力 都不能提供向心力（向心力沿水平方向），只有唱片對物塊 的靜摩擦力充當(dāng)向心力。 建立方程： 問題思考：轉(zhuǎn)盤的轉(zhuǎn)速達(dá)多大時(shí)，物塊與轉(zhuǎn)盤發(fā)生相對運(yùn)動(dòng)？（物塊與轉(zhuǎn)盤間的最大靜摩擦因數(shù)為） 2）彈力提供向心力： ①圓筒勻速轉(zhuǎn)動(dòng)，物體與筒壁相對靜止隨之做勻速圓周運(yùn)動(dòng)， 圓筒半徑為R，向心力

2、由彈力提供。 分析：受力分析如圖2，重力和靜摩擦力在豎直方向平衡， 筒壁對物塊的水平方向彈力提供物塊做勻速圓周運(yùn)動(dòng)的向 心力。 建立方程： 問題思考：為使物塊不滑落，圓筒的轉(zhuǎn)速至少為多少？ ②用細(xì)繩系著的小球在光滑水平面內(nèi)做勻速圓周運(yùn)動(dòng)， 受力如圖3，向心力由繩的彈力提供 建立方程： 問題思考：為使M在豎直方向保持平衡，m的角速 度為多少？ 2、合力提供向心力 （1）圓錐擺模型：質(zhì)量為m的小球用長為L的上端固定的 細(xì)線連接，使小球在水平面內(nèi)做勻速圓周運(yùn)動(dòng)，細(xì)線與豎 直方向夾角為 分析：對小球而言，受力如圖4，重力和繩拉力的合力 提供

3、向心力，其大小為，小球沿水平方向做勻速 圓周運(yùn)動(dòng)的半徑 建立方程： 整理得： 問題思考：此時(shí)繩的拉力和小球的線速度多大？ （2)火車轉(zhuǎn)彎問題 1)內(nèi)外軌等高時(shí)向心力的來源：外軌對輪緣的彈力提供向心力 受力分析：重力、支持力、外軌對輪緣的彈力，重力和支持力平衡，彈力提供向心力。 由于該彈力是由輪緣和外軌的擠壓產(chǎn)生的，且由于火車質(zhì)量很大，故輪緣和外軌間的相互作用力很大，易損害鐵軌。 2）實(shí)際中的火車轉(zhuǎn)彎 實(shí)際的轉(zhuǎn)彎處是外軌略高于內(nèi)軌，把火車當(dāng)作質(zhì)點(diǎn)，在水平面內(nèi)做圓周運(yùn)動(dòng)。 受力分析如圖5：支持力FN的方向不再是豎直的，而是垂直軌道平面斜向 彎道的內(nèi)側(cè)，支持力與重

4、力的合力F水平指向圓心，提供火車拐彎的向心力。 如內(nèi)外軌高度差，車速關(guān)系合適時(shí)，軌道受的側(cè)壓力等于零，重力和 支持力的合力完全提供轉(zhuǎn)彎時(shí)所需要的向心力，這樣外軌就不受輪緣的擠壓了。 根據(jù)牛頓第二定律得： mgtanθ＝m（r是轉(zhuǎn)彎處軌道所在的水平圓周的半徑，是使內(nèi)外軌均不受力的最佳速度） 變式訓(xùn)練：如圖6所示，已知繩長為L=20cm，水平桿長d=0.1m， 小球質(zhì)量m=0.3kg，整個(gè)裝置可以繞豎直軸轉(zhuǎn)動(dòng)，問： （1）要使繩子與豎直方向成角，試求該裝置必須以多大的角 速度轉(zhuǎn)動(dòng)才行？（答案：） （2）此時(shí)繩子的拉力為多大？（答案：） 小結(jié)： 1、解決圓周運(yùn)動(dòng)問題的關(guān)鍵是從“供”“需”兩方面來進(jìn)行研究 “供”——分析物體受力，求沿半徑方向指向圓心的合外力。 “需”——確定物體圓周軌道平面，定圓心、找半徑，用公式求出所需向心力。 “供”“需”平衡做圓周運(yùn)動(dòng)據(jù)列方程。 2、運(yùn)用向心力公式解決圓周運(yùn)動(dòng)問題的解題步驟： （1）明確研究對象，確定它做圓周運(yùn)動(dòng)的軌道平面，找到圓心和半徑，確定所需要的向心力方向和大小。 （2）確定研究對象在某個(gè)位置所處的狀態(tài)，進(jìn)行具體的受力分析，確定向心力的來源。 （3）建立以向心力方向?yàn)檎较虻淖鴺?biāo)，據(jù)牛頓第二定律列方程。 （4）解方程，對結(jié)果進(jìn)行必要的討論。