《重慶市九年級數(shù)學(xué)上冊 第23章 圖形的相似 23.4 中位線教案 （新版）華東師大版》由會(huì)員分享，可在線閱讀，更多相關(guān)《重慶市九年級數(shù)學(xué)上冊 第23章 圖形的相似 23.4 中位線教案 （新版）華東師大版（3頁珍藏版）》請?jiān)谘b配圖網(wǎng)上搜索。
1、重慶市九年級數(shù)學(xué)上冊 第23章 圖形的相似 23.4 中位線教案 （新版）華東師大版
課題名稱
中位線
三維目標(biāo)
1、知識(shí)與技能：
①了解三角形中位線的概念，探索并掌握三角形中位線的性質(zhì)。
②能應(yīng)用三角形中位線的性質(zhì)解決有關(guān)的推理與計(jì)算問題。
2、過程與方法：經(jīng)歷操作、觀察、猜想、探索發(fā)現(xiàn)后運(yùn)用旋轉(zhuǎn)變換進(jìn)行論證，肯定結(jié)論，再應(yīng)用結(jié)論解決問題的知識(shí)形成過程。
3、情感、態(tài)度與價(jià)值觀：從客觀實(shí)際中探索發(fā)現(xiàn)，再應(yīng)用于解決某些實(shí)際問題，體驗(yàn)數(shù)學(xué)源于實(shí)際，用于實(shí)際，感受學(xué)習(xí)的價(jià)值，培養(yǎng)學(xué)習(xí)自覺性和數(shù)學(xué)應(yīng)用意識(shí)。
重點(diǎn)目標(biāo)
三角形中位線的性質(zhì)及其應(yīng)用
難點(diǎn)目標(biāo)
三角形中位線定理的推
2、導(dǎo)及如何添加輔助線
導(dǎo)入示標(biāo)
1.了解三角形中位線的概念，探索并掌握三角形中位線的性質(zhì)。
2.能應(yīng)用三角形中位線的性質(zhì)解決有關(guān)的推理與計(jì)算問題。
目標(biāo)三導(dǎo)
學(xué)做思一：
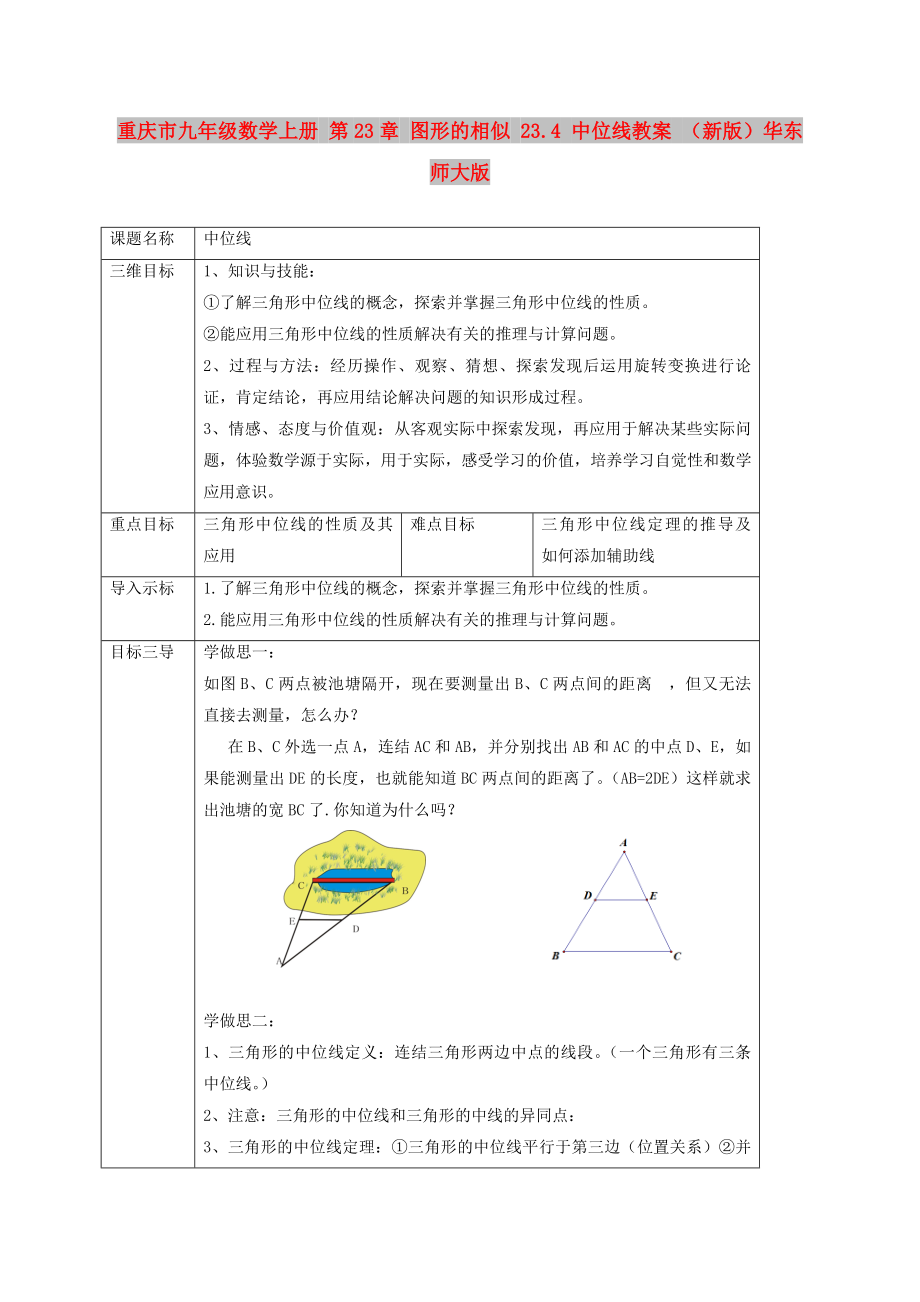
如圖B、C兩點(diǎn)被池塘隔開，現(xiàn)在要測量出B、C兩點(diǎn)間的距離?，但又無法直接去測量，怎么辦？?
在B、C外選一點(diǎn)A，連結(jié)AC和AB，并分別找出AB和AC的中點(diǎn)D、E，如果能測量出DE的長度，也就能知道BC兩點(diǎn)間的距離了。（AB=2DE）這樣就求出池塘的寬BC了.你知道為什么嗎？
學(xué)做思二：
1、三角形的中位線定義：連結(jié)三角形兩邊中點(diǎn)的線段。（一個(gè)三角形有
3、三條中位線。）
2、注意：三角形的中位線和三角形的中線的異同點(diǎn)：
3、三角形的中位線定理：①三角形的中位線平行于第三邊（位置關(guān)系）②并且等于第三邊的一半（數(shù)量關(guān)系）
符號(hào)語言表述：∵DE是△ABC的中位線（或AD=BD,AE=CE) ∴DEBC
4、定理的推導(dǎo)：（先獨(dú)立思考，再合作交流，掌握多種證明方法）
學(xué)做思三：
例1.已知：如圖所示，在四邊形ABCD中，E、F、G、H分別是AB、BC、CD、DA的中點(diǎn)．?求證：四邊形EFGH是平行四邊形．（用一句話歸納此題）
例2：已知 如圖 △ABC中，AB=5cm ， BC=9cm, BE是∠ABC的平分線，過點(diǎn)A作BE
4、的垂線，垂足為E，延長AE交BC于F，P是AC邊的中點(diǎn)，求EF的長。
達(dá)標(biāo)檢測
1、如圖1，在△ABC中，D，E分別是AB，AC的中點(diǎn)，DE=10，則BC=_______．
（1） （2）
2、已知三角形的三邊長分別是4，5，6，則它的三條中位線圍成的三角形的周長是________
3、如圖2，點(diǎn)D，E，F(xiàn)分別是△ABC三邊的中點(diǎn)，且S△DEF=3，則△ABC的面積等于（ ）
A．6 B．9 C．12 D．15
反思總結(jié)
1.知識(shí)建構(gòu)
2.能力提高
3.課堂體驗(yàn)
課后練習(xí)
重慶市九年級數(shù)學(xué)上冊 第23章 圖形的相似 23.4 中位線教案 （新版）華東師大版
