《2018屆中考數(shù)學(xué)專項復(fù)習(xí) 圓與解直角三角形的綜合練習(xí)》由會員分享，可在線閱讀，更多相關(guān)《2018屆中考數(shù)學(xué)專項復(fù)習(xí) 圓與解直角三角形的綜合練習(xí)（3頁珍藏版）》請在裝配圖網(wǎng)上搜索。
1、
圓與解直角三角形的綜合
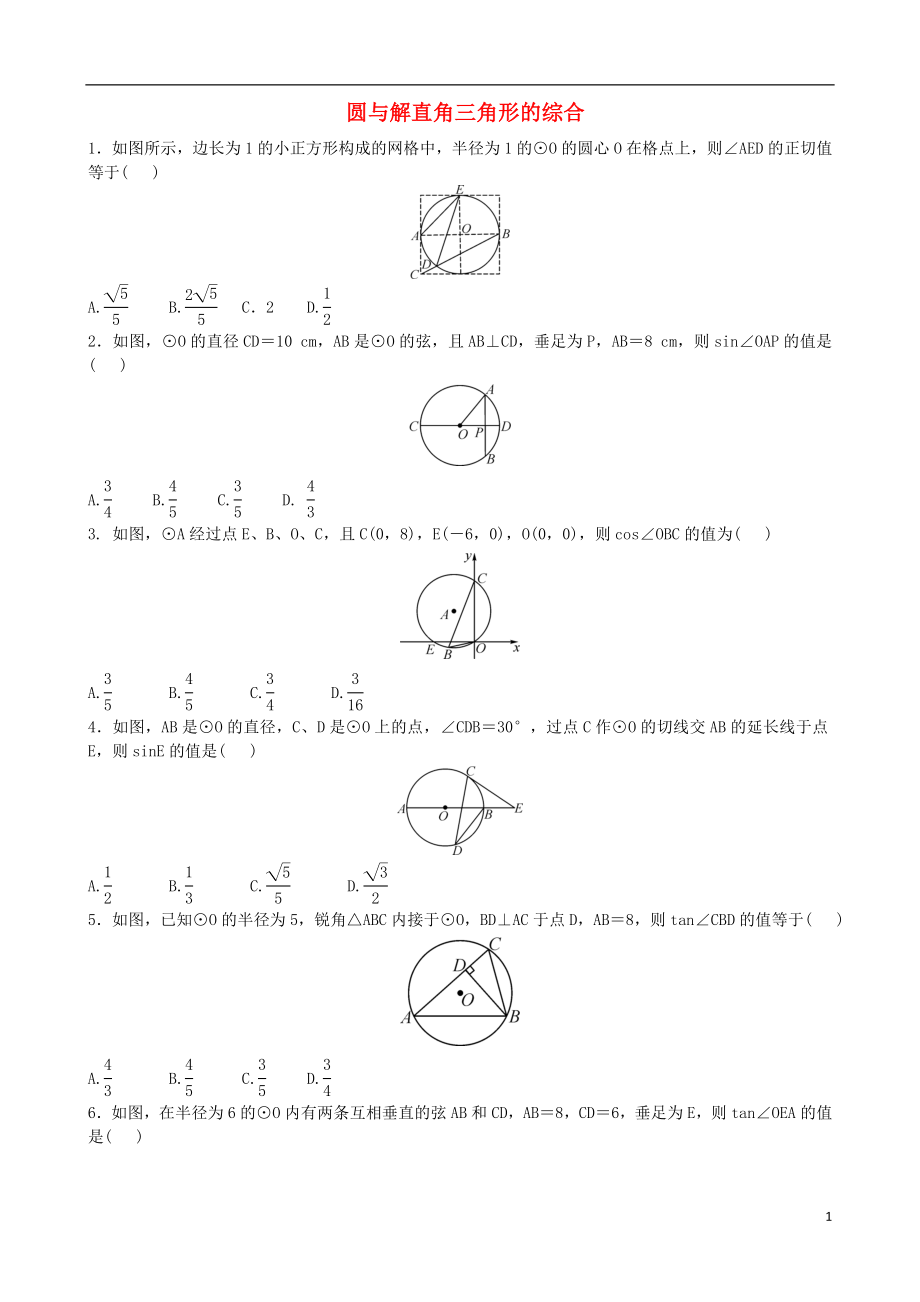
1．如圖所示，邊長為1的小正方形構(gòu)成的網(wǎng)格中，半徑為1的⊙O的圓心O在格點上，則∠AED的正切值等于( )
A. B. C．2 D.
2．如圖，⊙O的直徑CD＝10 cm，AB是⊙O的弦，且AB⊥CD，垂足為P，AB＝8 cm，則sin∠OAP的值是( )
A. B. C. D.
3. 如圖，⊙A經(jīng)過點E、B、O、C，且C(0，8)，E(－6，0)，O(0，0)，則cos∠OBC的值為( )
A. B. C. D.
4．如圖，AB是⊙O的直徑，C
2、、D是⊙O上的點，∠CDB＝30°，過點C作⊙O的切線交AB的延長線于點E，則sinE的值是( )
A. B. C. D.
5．如圖，已知⊙O的半徑為5，銳角△ABC內(nèi)接于⊙O，BD⊥AC于點D，AB＝8，則tan∠CBD的值等于( )
A. B. C. D.
6．如圖，在半徑為6的⊙O內(nèi)有兩條互相垂直的弦AB和CD，AB＝8，CD＝6，垂足為E，則tan∠OEA的值是( )
A. B. C. D.
7．如圖，△ABC內(nèi)接于⊙O，連結(jié)OA、OC，⊙O的半徑為3，且si
3、nB＝ ，則弦AC的長為( )
A. B．5 C. D.
8．如圖，以點O為圓心的兩個圓中，大圓的弦AB切小圓于點C，OA交小圓于點D，若OD＝2，tan∠OAB＝，則AB的長是 ____．
9．在半徑為1的⊙O中，弦AB、AC的長分別為1和 ，則∠BAC的度數(shù)為 ．
10．在△ABC中，AB＝AC＝10，cosB＝ ，如果圓O的半徑為2，
且經(jīng)過點B、C，那么線段AO的長等于 __________．
11．如圖所示，以銳角△ABC的邊AB為直徑作⊙O，交AC、BC于E、
D兩點，若AC＝14，CD＝4，7
4、sinC＝3tanB，則BD＝ _____．
12. 如圖所示，在⊙O中，直徑AB＝6，AB與弦CD相交于點E，連結(jié)AC、BD，若AC＝2，則cosD的值為____．
13. 如圖，已知AB是圓O的直徑，弦CD⊥AB，垂足為H，與AC平行的圓O的一條切線交CD的延長線于點M，交AB的延長線于點E，切點為F，連結(jié)AF交CD于點N.
(1)求證：CA＝CN；
(2)連結(jié)DF，若cos∠DFA＝ ，AN＝2 ，求⊙O的直徑的長度．
參考答案：
1---7 DCAAD DB
8. 8
9. 15°或105°
10. 6或10
11.
5、 6
12.
13. 解：(1)證明：連結(jié)OF，則∠OAF＝∠OFA.
∵M(jìn)E與⊙O相切，∴OF⊥ME.∵CD⊥AB，
∴∠M＋∠FOH＝180°.
∵∠BOF＝∠OAF＋∠OFA＝2∠OAF，∠FOH＋∠BOF＝180°，
∴∠M＝2∠OAF.
∵M(jìn)E∥AC，∴∠M＝∠ACM＝2∠OAF.∵CD⊥AB，
∴∠ANC＋∠OAF＝∠BAC＋∠ACM＝90°，
∴∠ANC＝90°－∠OAF，∠BAC＝90°－∠ACM＝90°－2∠OAF，
∴∠CAN＝∠OAF＋∠BAC＝90°－∠OAF＝∠ANC，∴CA＝CN.
(2)連結(jié)OC.
∵cos∠DFA＝，∠DFA＝∠ACH，
∴＝.
設(shè)CH＝4a，則AC＝5a，AH＝3a.
∵CA＝CN，∴NH＝a.
∴AN＝＝a＝2，
∴a＝2，AH＝3a＝6，CH＝4a＝8.
設(shè)圓的半徑為r，則OH＝r－6.
在Rt△OCH中，∵OC2＝CH2＋OH2，OC＝r，
CH＝8，OH＝r－6，
∴r2＝82＋(r－6)2，解得r＝.
∴⊙O的直徑的長度為2r＝.
3
2018屆中考數(shù)學(xué)專項復(fù)習(xí) 圓與解直角三角形的綜合練習(xí)
