2017年度 江西省重點中學協(xié)作體高三下學期第一次聯(lián)考數(shù)學（文）試題

《2017年度 江西省重點中學協(xié)作體高三下學期第一次聯(lián)考數(shù)學（文）試題》由會員分享，可在線閱讀，更多相關《2017年度 江西省重點中學協(xié)作體高三下學期第一次聯(lián)考數(shù)學（文）試題（10頁珍藏版）》請在裝配圖網(wǎng)上搜索。

1、 2017屆江西省重點中學協(xié)作體高三下學期第一次聯(lián)考數(shù)學（文）試題 考試用時：120分 全卷滿分：150分 一、選擇題 (在每小題給出的四個選項中，只有一項是符合題目要求的，請把正確答案的代號填在題后的括號內(nèi),每小題5分，共60分） 1.已知集合，集合，則（ ） A． B． C． D． 2.為虛數(shù)單位，復數(shù)的虛部為（ ） A． 1 B．0 C． D．以上都不對 3． 已知平面直角坐標系內(nèi)的兩個向量，，且平面內(nèi)的任一向量都可以 唯一的表示成（為實數(shù)），則的取值范圍是（ ）

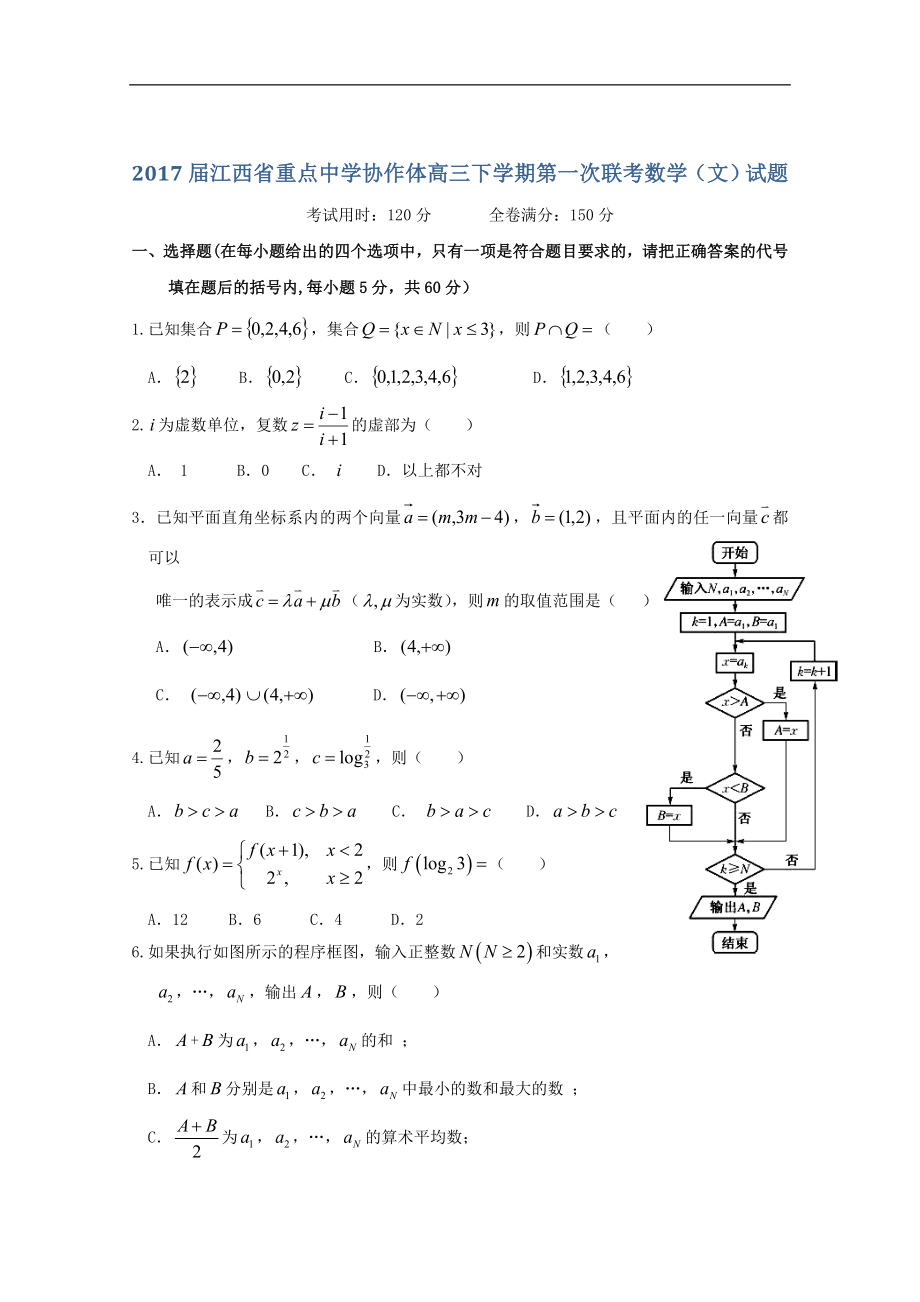
2、 A． B． C． D． 4.已知，，，則（ ） A． B． C． D． 5.已知，則（ ） A．12 B．6 C．4 D．2 6.如果執(zhí)行如圖所示的程序框圖，輸入正整數(shù)和實數(shù)， ，…，，輸出，，則（ ） A．+為，，…，的和 ； B．和分別是，，…，中最小的數(shù)和最大的數(shù) ； C．為，，…，的算術平均數(shù)； D．和分別是，，…，中最大的數(shù)和最小的數(shù) . 7.某企業(yè)節(jié)能降耗技術改造后，

3、在生產(chǎn)某產(chǎn)品過程中的產(chǎn)量（噸）與相應的生產(chǎn)能耗（噸） 的幾組對應數(shù)據(jù)如表所示： 3 4 5 6 2.5 3 4 若根據(jù)表中數(shù)據(jù)得出關于的線性回歸方程為，若生產(chǎn)7噸產(chǎn)品，預計 相應的生產(chǎn)能耗為（ ）噸. A． 5.25 B． 5.15 C． 5.5 D．9.5 8.設當時，函數(shù)取得最大值，則= (?? ) A． B． C． D． 9.設表示不同直線，表示不同平面，則下列結論中正確的是(　 　) A．若 則 B．

4、若，則 C．若 則 D．若則 10.過函數(shù)圖像上一個動點作函數(shù)的切線，則切線傾斜角的范圍為(?? ) A． B． C． D． 11.等差數(shù)列的前項和為，若公差，則（　　） A． B． C． D． 12.我國古代數(shù)學家祖暅是著名數(shù)學家祖沖之之子，祖暅原理敘述道 :“夫疊棋成立積，緣冪勢既同，則積不容異?！币馑际牵簥A在兩個平行平面之間的兩個幾何體被平行于這兩個平行平面的任意平面所截，如果截得的兩個截面面積總相等，那么這兩個幾何體的體積相等。其最著名之處是解決了“牟合方蓋”中的體積問題，其核心過程為：如下圖正方體 ，

5、求圖中四分之一圓柱體和四分之一圓柱體公共部分的體積 ，若圖中正方體的棱長為2，則（ ） （在高度 處的截面：用平行于正方體上下底面的平面去截，記截得兩圓柱體公共部分所得面積為 ，截得正方體所得面積為 ，截得錐體所得面積為 ， ） C1 A． B． C． D． 二、填空題(每小題5分，共20分，請把正確答案填在題中橫線上) 13.,使得成立，則實數(shù)的取值范圍為. 14.已知等比數(shù)列滿足：，，則. 15.已知實數(shù)滿足，若使得取得最小值的可行解有無數(shù)個，則實數(shù) 的值為__________． 16. 已

6、知雙曲線的右焦點為設為雙曲線上關于原點對稱的 兩點，且滿足，若直線的斜率為,則雙曲線的離心率為 . 三、解答題(本大題共6小題，共70分，解答寫出必要的文字說明、演算過程及步驟) 17.（本小題滿分12分） 如圖，是等腰直角三角形，,點在邊的延長線上，且， . （1）求的值； （2）求的長. 18.（本小題滿分12分） 如圖一，在邊長為2的等邊三角形中，、、分別是、、的 中點，將沿折起，得到如圖二所示的三棱錐，其中. （1）證明：； （2）求四棱錐的體積.

7、 19.（本小題滿分12分） 某高校要了解在校學生的身體健康狀況，隨機抽取了50名學生進行心率測試，心率全部介于50次/分到75次/分之間，現(xiàn)將數(shù)據(jù)分成五組，第一組，按上述分組方法得到的頻率分布直方圖如圖所示，已知圖中從左到右的前三組的頻率之比為:4:10. （1）求的值. （2）若從第一、第五組兩組數(shù)據(jù)中隨機抽取兩名學生的心率，求這兩個心率之差的絕對值大于5的概率. 20.（本小題滿分12分） 已知橢圓的離心率為，以原點為圓心，橢圓的短半軸長為半徑的圓與直線相切． （1）求橢圓的方程； （2） 分別為橢圓的左、右

8、頂點，動點滿足，直線與橢圓交于點（與 點不重合），以為直徑的圓交線段于點，求證：直線過定點． 21.（本小題滿分12分） 設是定義在上的函數(shù)，若存在，使得在上單調(diào)遞增，在上單調(diào)遞減，則稱為上的函數(shù). (1)已知為上的函數(shù)，求的取值范圍； （2）設，其中，判斷是否為上的函數(shù)？ （3）已知為上的函數(shù)，求的取值范圍. 四、請考生在第22、23題中任選一題作答，如果多做，則按所做的第一題計分，做答時請寫清題號. 22．（本小題滿分10分）選修

9、4-4：坐標系與參數(shù)方程 在平面直角坐標系中，以坐標原點為極點，軸的非負半軸為極軸建立極坐標系.已知曲線 ，曲線（為參數(shù)）. (1)求曲線的直角坐標方程； （2）若曲線與曲線相交于、兩點，求的值. 23.（本小題滿分10分）選修4-5：不等式選講 已知函數(shù)． （1）求不等式的解集； （2）若函數(shù)的最小值為，且，求的 取值范圍. 江西省重點中學協(xié)作體2017屆高三第一次聯(lián)考 數(shù)學（文科）答案 BACC BDAD DBBA 13.或 14. 15. 或

10、16. 17.解：（1）因為為等腰直角三角形，所以， 又，所以， ………………………………………………3分 在中，由正弦定理得 ，即………………………………6分 （2） 設，則，在中： ，即， ，即 ……………………………………………………12分 18.解：（1）∵平面BDC 且BC 平面 BDC …………………………………………6分 （2）在中，， ∵， ∴ ………………………12分 19. 解：（1）因為第二組數(shù)據(jù)的頻率為 0.032×5=0.16，故第二組的頻數(shù)為

11、0.16×50=8， 第一組的頻數(shù)為2，第三組的頻數(shù)為20，第四組的頻數(shù)為16，第五組的頻數(shù)為4 所以 2=50-20-16-8-4=2. …………………………………………6分 (2) 第一組的數(shù)據(jù)有2個，第五組的數(shù)據(jù)有4個，故總的基本事件有15個， 符合題意的基本事件有8個， 所以這兩個心率之差的絕對值大于5的概率. ………………………12分 20.解：（1）由題知，原點到直線的距離 又，則 ∴橢圓方程為 ……………………………………5分 （2）設，則直線的

12、方程為： 聯(lián)立消去得， ……………………7分 ，則 故 ………………………………9分 又以為直徑的圓上與線段交于點，則 故直線方程為，即 ∴直線過定點． ………………………………………………………12分 21.解：（1），令………3分 又在上為單調(diào)遞增，在上單調(diào)遞減， 為函數(shù)…………………………………………………4分 （2）， 在上為單調(diào)遞減，……………………………………………………6分 又， ，使得，

13、 在上為單調(diào)遞增，在上單調(diào)遞減， 是上的函數(shù) ……………………………………………8分 （3） 方程的判別式為 當即時，恒成立， 此時時，，單調(diào)遞減；時，，單調(diào)遞增； 故不是函數(shù)。 ……………………………………………………9分 當即時， 方程的兩根分別為， 顯然，且 在和上為減,在和上為增 所以是在(且)上的函數(shù). 綜上所述，若為上的函數(shù)，則的取值范圍為…………12分 22.解：(1)由 ， 所以曲線的直角坐標方程為： …………………………5分 （2）聯(lián)解， 設，為方程的兩根，有， ……………………………………10分 23. 解：(1) 的解集為 ………………………………………5分 （2）由條件得，當且僅當時， 其最小值，即． 又， 故的取值范圍為 此時，．……………………………………………10分