《廣東省廣州市花都區(qū)赤坭中學(xué)九年級數(shù)學(xué)上冊24.1.1圓垂徑定理學(xué)案無答案新版新人教版》由會員分享,可在線閱讀�,更多相關(guān)《廣東省廣州市花都區(qū)赤坭中學(xué)九年級數(shù)學(xué)上冊24.1.1圓垂徑定理學(xué)案無答案新版新人教版(3頁珍藏版)》請?jiān)谘b配圖網(wǎng)上搜索。
1����、
垂徑定理
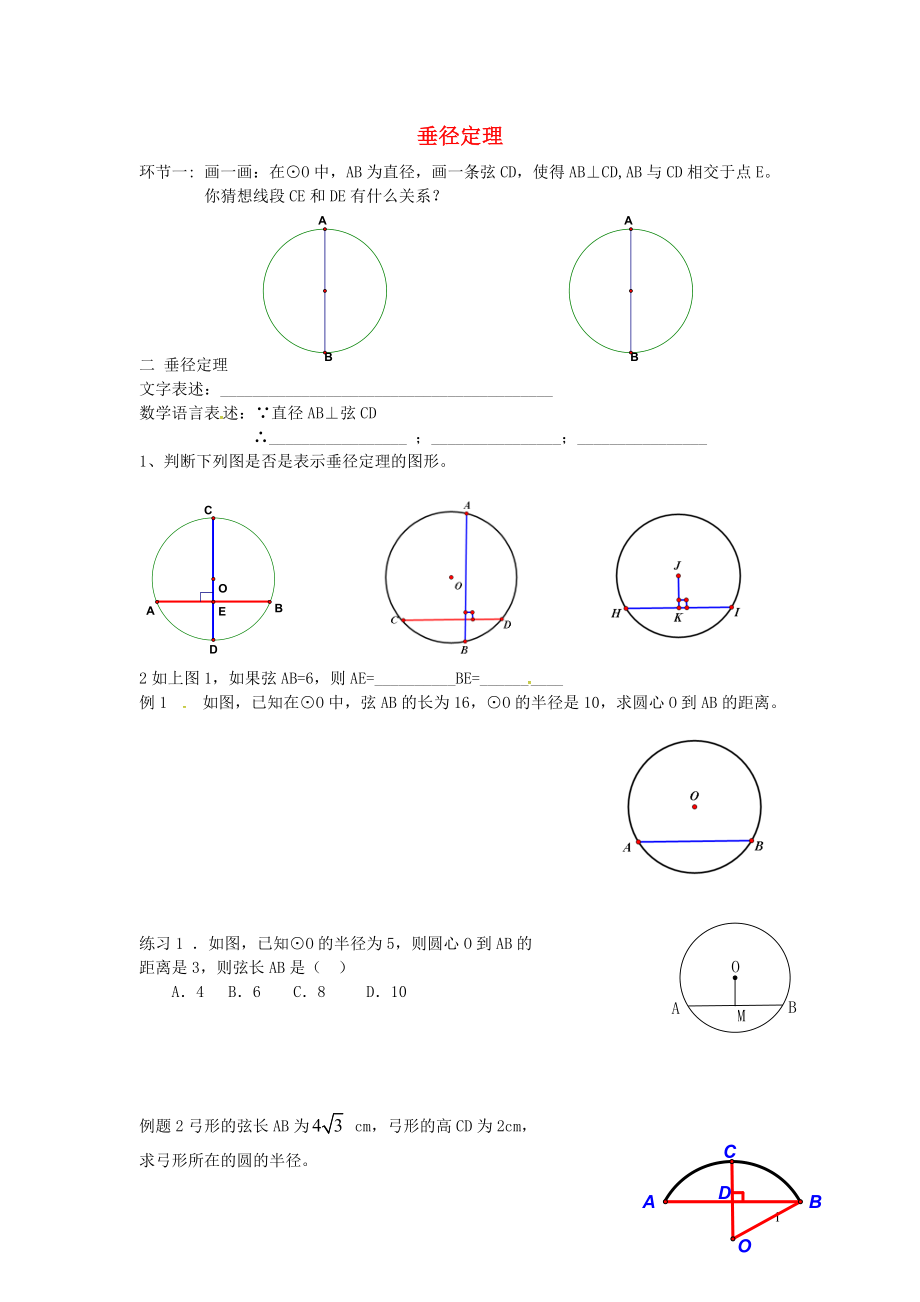
環(huán)節(jié)一: 畫一畫:在⊙O中����,AB為直徑,畫一條弦CD�,使得AB⊥CD,AB與CD相交于點(diǎn)E。
你猜想線段CE和DE有什么關(guān)系��?
二 垂徑定理
文字表述:_________________________________________
數(shù)學(xué)語言表述:∵直徑AB⊥弦CD
∴_________________ �����;________________���;________________
1�、判斷下列圖是否是表示垂徑定理的圖形����。
2如上圖1�����,如果弦AB=6�����,則AE
2����、=__________BE=__________
例1 如圖��,已知在⊙O中�����,弦AB的長為16��,⊙O的半徑是10����,求圓心O到AB的距離。
練習(xí)1 .如圖,已知⊙O的半徑為5�����,則圓心O到AB的
距離是3���,則弦長AB是( )
A.4 B.6 C.8 D.10
例題2弓形的弦長AB為 cm����,弓形的高CD為2cm�,
求弓形所在的圓的半徑。
解:
練習(xí)2�����、如圖:某公園的一座石拱橋是圓弧形(劣?�。┢淇缍葹锳B=24米�����,拱的半徑為13米�����,則拱高CD為 ����;
拓展:在直徑
3、是10cm的⊙O中���,CD ⊥ AB ���,垂足為E ,
已知 CD=8 求AE的長?
課后作業(yè)
1如圖����,AB是圓O的直徑,CD是弦�,CD⊥AB,
判斷下列結(jié)論是否正確。
①CE=DE ② ∠COE=∠DOE
③ AC=AD ④ AE=0E
2 .如圖��,已知圓心O到AB的距離是1cm����,
弦AB的是4cm, 則AM=__________����;
⊙O的半徑為___________
3已知:如圖����,在以O(shè)為圓心的兩個同心圓中�,大圓的弦AB交小圓于C,D兩點(diǎn)�。
求證:AC=BD。
4����、思考 如圖,點(diǎn)P在AB上運(yùn)動�����,AO=5�����,AB=8,
當(dāng)P點(diǎn)在何處時��,PO的距離最小_____ 此時OP=_______
當(dāng)P點(diǎn)在何處時���,PO的距離最大_______. 此時OP=_______
前置作業(yè)
1預(yù)習(xí)書本P80頁----P82頁“垂直于弦的直徑”
2圓是軸對稱圖形,也是______圖形 ��,
圓有_______條對稱軸,這些對稱軸有何特點(diǎn)________________
3判斷正誤 弦是直徑( ) 直徑是弦 ( )
4如右圖���,在Rt△ABC中����,a, b ,c是它的三條邊�,
勾股定理:_________________
在Rt△ABC中,300所對的直角邊長是斜邊的________
5練習(xí)
①如果 BC=2, AC = 4, AB=___________
②如果BC=1, AB = 3, AC=___________
③如果∠A=300 �,AC = ,則BC=____
解�����,設(shè)BC=x, 則AB= ____��,
由勾股定理可列式:
3
 廣東省廣州市花都區(qū)赤坭中學(xué)九年級數(shù)學(xué)上冊24.1.1圓垂徑定理學(xué)案無答案新版新人教版
廣東省廣州市花都區(qū)赤坭中學(xué)九年級數(shù)學(xué)上冊24.1.1圓垂徑定理學(xué)案無答案新版新人教版