《2014屆高考數(shù)學總復習 課時提升作業(yè)(四十) 第七章 第一節(jié) 文》由會員分享���,可在線閱讀���,更多相關《2014屆高考數(shù)學總復習 課時提升作業(yè)(四十) 第七章 第一節(jié) 文(6頁珍藏版)》請在裝配圖網(wǎng)上搜索���。
1���、課時提升作業(yè)(四十)
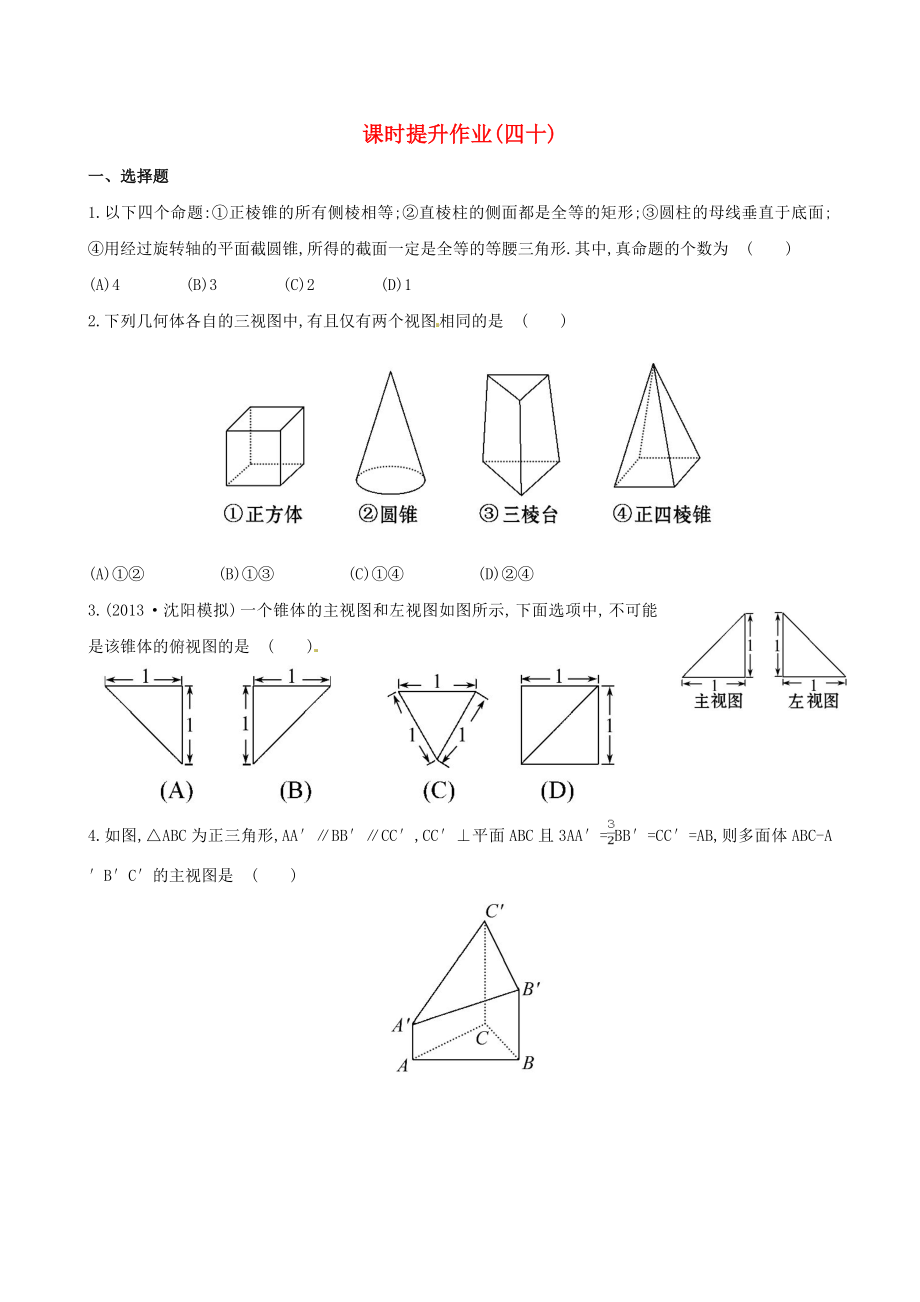
一���、選擇題
1.以下四個命題:①正棱錐的所有側棱相等;②直棱柱的側面都是全等的矩形;③圓柱的母線垂直于底面;④用經(jīng)過旋轉軸的平面截圓錐,所得的截面一定是全等的等腰三角形.其中,真命題的個數(shù)為 ( )
(A)4 (B)3 (C)2 (D)1
2.下列幾何體各自的三視圖中,有且僅有兩個視圖相同的是 ( )
(A)①② (B)①③ (C)①④ (D)②④
3.(2013·沈陽模擬)一個錐體的主視圖和左視圖如圖所示,下面選項中,不可能是該錐體的俯視圖的是 ( )
4.如圖,△ABC為正三角形,AA′∥BB′∥CC′,CC′
2、⊥平面ABC且3AA′=BB′=CC′=AB,則多面體ABC-A′B′C′的主視圖是 ( )
5.(2013·寧波模擬)一個水平放置的平面圖形的斜二測直觀圖是直角梯形(如圖所示),∠ABC=45°,AB=AD=1,DC⊥BC,則這個平面圖形的面積為 ( )
(A)+ (B)2+
(C)+ (D)+
6.一個正方體截去兩個角后所得幾何體的主視圖���、左視圖如圖所示,則其俯視圖為 ( )
7.(2013·西安模擬)一只螞蟻從正方體ABCD-A1B1C1D1的頂點A處出發(fā),經(jīng)正方體的表面,按最短路線爬行到達頂點C1位置,則下列圖形中可以表示
3���、正方體及螞蟻最短爬行路線的主視圖是 ( )
(A)①② (B)①③ (C)②④ (D)③④
二、填空題
8.等腰梯形ABCD,上底CD=1,腰AD=CB=,下底AB=3,以下底所在直線為x軸,則由斜二測畫法畫出的直觀圖A′B′C′D′的面積為 .
9.(2013·德州模擬)一個正三棱柱的側棱長和底面邊長相等,體積為2,它的三視圖中的俯視圖如圖所示,左視圖是一個矩形,則這個矩形的面積是 .
10.(2013·合肥模擬)一個三棱錐的主視圖和左視圖及其尺寸
如圖所示,則該三棱錐的俯視圖的面積為 .
三���、解答題
11.(能力挑戰(zhàn)題)某幾何體的一條
4���、棱長為,在該幾何體的主視圖中,這條棱的投影是長為的線段,在該幾何體的左視圖與俯視圖中,這條棱的投影分別是長為a和b的線段,求a+b的最大值.
答案解析
1.【解析】選B.由正棱錐的定義可知所有側棱相等,故①正確;由于直棱柱的底面的各邊不一定相等,故側面矩形不一定全等,因此②不正確;由圓柱母線的定義可知③正確;結合圓錐軸截面的作法可知④正確.綜上,正確的命題有3個.
2.【解析】選D.在各自的三視圖中,①正方體的三個視圖都相同;②圓錐的兩個視圖相同;③三棱臺的三個視圖都不同;④正四棱錐的兩個視圖相同,故選D.
【變式
5、備選】正三棱柱(底面為正三角形的直棱柱)ABC-A1B1C1如圖所示,以四邊形ABB1A1為水平面,四邊形BCC1B1的前面為正前方畫出的三視圖正確的是 ( )
【解析】選A.矩形BCC1B1的前面為正前方,故主視圖為矩形,左側為△ABC,所以左視圖為三角形.俯視圖為兩個有公共邊的矩形,公共邊為CC1在面ABB1A1內的投影,故選A.
3.【解析】選C.當俯視圖為A,B時表示底面為等腰直角三角形,且過直角頂點的棱與底面垂直的三棱錐.當俯視圖為D時,表示底面為正方形,且有一條側棱與底面垂直的四棱錐.故選C.
【方法技巧】由直觀圖畫三視圖的技巧
(1)可以想象將一幾何體放在自己面
6���、前,然后從正前方,左側及上面觀察該幾何體,進而得到主視圖���、左視圖和俯視圖.
(2)在畫三視圖時,要注意看得見的輪廓線畫成實線,看不見的輪廓線畫成虛線.
4.【解析】選D.由AA′∥BB′∥CC′及CC′⊥平面ABC,知AA′⊥平面ABC,
BB′⊥平面ABC.又CC′=BB′=3AA′,且△ABC為正三角形,故主視圖應為D中的圖形.
5.【解析】選B.如圖將直觀圖ABCD還原后為直角梯形
A′BCD′,其中
A′B=2AB=2,BC=1+,A′D′=AD=1,
∴S=×(1+1+)×2=2+.
6.【解析】選C.依題意可知該幾何體的直觀圖如圖所示,故其俯視圖應為C.
7.
7���、【解析】選C.依題意得,題中提供的選項中,圖②④可以表示正方體及螞蟻最短爬行路線的主視圖,選C.
8.【解析】如圖所示,∵OE==1,
∴O′E′=,E′F′=,
∴直觀圖A′B′C′D′的面積為S′=×(1+3)×=.
答案:
9.【解析】設正三棱柱的底面邊長為a,利用體積為2,很容易求出這個正三棱柱的底面邊長和側棱長都是2,所以底面正三角形的高為,故所求矩形的面積為2.
答案:2
10.【解析】由題意可知,該三棱錐的俯視圖是一個底邊長為2,高為1的三角形,則其面積為1.
答案:1
11.【思路點撥】可將該幾何體放在長方體中,且已知長為的棱為長方體的體對角線來解決.
【解析】如圖,把幾何體放到長方體中,使得長方體的體對角線剛好為幾何體的已知棱,則長方體的體對角線A1C=,則它的主視圖投影長為A1B=,左視圖投影長為A1D=a,俯視圖投影長為A1C1=b,則a2+b2+()2=2×()2,即a2+b2=8,
又≤,當且僅當“a=b=2”時等號成立.
∴a+b≤4,即a+b的最大值為4.
 2014屆高考數(shù)學總復習 課時提升作業(yè)(四十) 第七章 第一節(jié) 文
2014屆高考數(shù)學總復習 課時提升作業(yè)(四十) 第七章 第一節(jié) 文