2022年高三數(shù)學(xué)上學(xué)期第三次月考試題 理(III)

《2022年高三數(shù)學(xué)上學(xué)期第三次月考試題 理(III)》由會(huì)員分享，可在線閱讀，更多相關(guān)《2022年高三數(shù)學(xué)上學(xué)期第三次月考試題 理(III)（6頁珍藏版）》請?jiān)谘b配圖網(wǎng)上搜索。

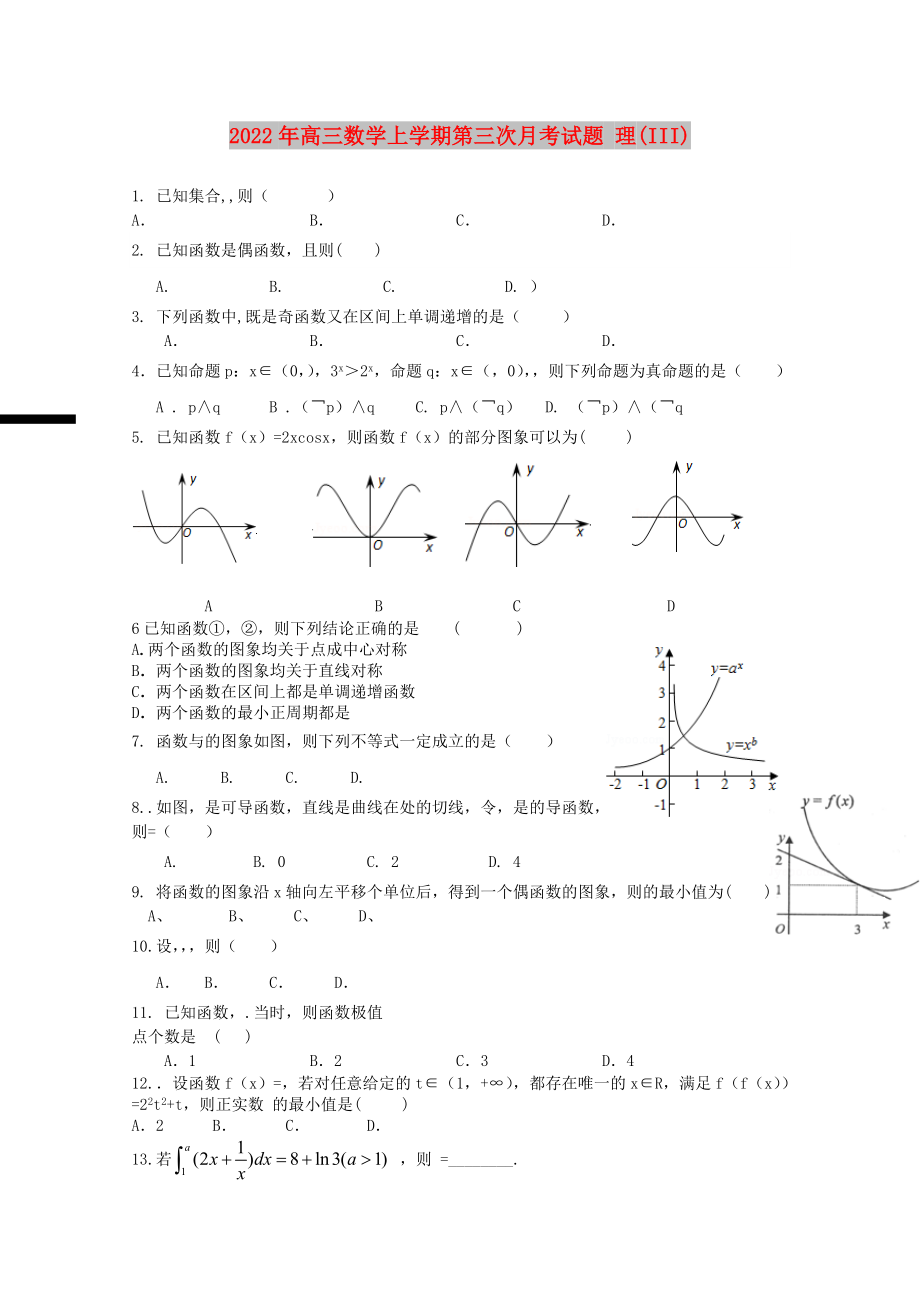
1、2022年高三數(shù)學(xué)上學(xué)期第三次月考試題 理(III) 1. 已知集合,,則（ ） A． B． C． D． 2. 已知函數(shù)是偶函數(shù)，且則( ) A. B. C. D. ） 3. 下列函數(shù)中,既是奇函數(shù)又在區(qū)間上單調(diào)遞增的是（ ） A． B． C． D． 4．已知命題p：x∈（0，），3x＞2x，命題q：x∈（，0），，則下列命題為真命題的是（　 ） A . p∧q B .（￢p）∧q C. p∧（￢q） D. （￢p）∧（￢q 5. 已知函數(shù)f（x）=

2、2xcosx，則函數(shù)f（x）的部分圖象可以為( ) A B C D 6已知函數(shù)①，②，則下列結(jié)論正確的是 ( ) A.兩個(gè)函數(shù)的圖象均關(guān)于點(diǎn)成中心對稱 B．兩個(gè)函數(shù)的圖象均關(guān)于直線對稱 C．兩個(gè)函數(shù)在區(qū)間上都是單調(diào)遞增函數(shù) D．兩個(gè)函數(shù)的最小正周期都是 7. 函數(shù)與的圖象如圖，則下列不等式一定成立的是（　?。? A. B. C. D. 8. .如圖，是可導(dǎo)函數(shù)，直線是曲線在處的切

3、線，令，是的導(dǎo)函數(shù)，則=（　?。? A. B. 0 C. 2 D. 4 9. 將函數(shù)的圖象沿x軸向左平移個(gè)單位后，得到一個(gè)偶函數(shù)的圖象，則的最小值為( ) 　A、　　　 B、　　 C、　　 D、 10.設(shè)，，，則（ ） A． B． C． D． 11. 已知函數(shù)，.當(dāng)時(shí)，則函數(shù)極值 點(diǎn)個(gè)數(shù)是 ( ) A．1 B．2 C．3 D．4 12. ．設(shè)函數(shù)f（x）=，若對任意給定的t∈（1，+∞），都存

4、在唯一的x∈R，滿足f（f（x））=22t2+t，則正實(shí)數(shù) 的最小值是( ) A．2 B． C． D． 13.若 ，則 =________. 14.設(shè)為銳角,若,則的值為______ 15.為了使函數(shù) 在區(qū)間[0，10]內(nèi)至少出現(xiàn)10次最大值，則 的最小值為______________. 16.已知正數(shù) 滿足 ，則 的最大值為___________. 1 2 3 4 5 6 7 8 9 10 11 12 13._________________14._________

5、_______15._____________________16._______________ 17.(本小題滿分10分)已知函數(shù)和的圖象關(guān)于軸對稱，且. （Ⅰ）求函數(shù)的解析式；（Ⅱ）解不等式 18. （本小題滿分12分） 已知向量，函數(shù)的圖象的對稱中心與對稱軸之間的最小距離為。 （1）求的值，并求函數(shù)f（x）在區(qū)間上的單調(diào)增區(qū)間； （2）△ABC中，角A，B，C的對邊分別為，b，c，f（A）＝1，cosC＝，求sinB?的值。 19. （本小題滿分12分）

6、已知函數(shù)． （I）求函數(shù)f（x）的解析式； （II）若在〔一〕內(nèi)，函數(shù)y＝f（x）十m有兩個(gè)零點(diǎn)，求實(shí)數(shù)m的取值范圍． 20.（ 本小題滿分l2分) 已知函數(shù)，在區(qū)間上有最大值4，最小值1，設(shè)． （1）求的值； （2）不等式在上恒成立，求實(shí)數(shù)的范圍； 21. (本小題滿分l2分) 已知函數(shù)，其中a為常數(shù)，且a＞0。 （1）若函數(shù)y＝f（x）在點(diǎn)（1，f（1）處的切線與直線y＝x＋1垂直，求函數(shù)f（

7、x）的單調(diào)遞減區(qū)間； （2）若函數(shù)f（x）在區(qū)間（0,2］上的最小值為，求a的值。 22.(本小題滿分l2分) 設(shè)函數(shù)f（x）＝ （I）求函數(shù)f（x）的極值； （II）已知g（x）＝f（x＋1），當(dāng)＞0時(shí)，若對任意的x≥0，恒有g(shù)（x））≥0，求實(shí)數(shù)的取值范圍． xx屆高三第三次月考（理科）數(shù)學(xué)答案 ADBCA CDBBD CB 13.3 14. 15. 16. 17. （Ⅰ） ………5分（Ⅱ） ………10分 18.解：（1）

8、 ……2分 由圖象的對稱中心與對稱軸之間的最小距離為，故… 4分 令 又 ， 所以所求單調(diào)增區(qū)間為 ……6分 （2） 或 ……8分 或 又 ……10分 12分 19. 解：（1）依題意， ，…3分 20. ……………3分 ……………..6分 所以： …………………..12分 21.解： ……1分 （1）因?yàn)榍€y＝f（x）在點(diǎn)（1，f（1）處的切線與直線y＝x＋1垂直，所以 ……3分 當(dāng)a=2時(shí)，，令，所以函數(shù)f（x）的單 調(diào)遞減區(qū)間為（0,2） ……5分 （2）當(dāng)0<<2,時(shí)，由 所以函數(shù)f（x）在（0，）上為減函數(shù)， 在（，2）上為增函數(shù)， ……9分 當(dāng) 時(shí)， 在（0,2）上恒成立，這時(shí)f（x）在（0,2] 上為減函數(shù) （舍去） ……11分 綜上知， ……12 22.解（1）由題意：f（x）＝的定義域（0， ，