《陜西省山陽縣色河鋪鎮(zhèn)2018年中考數(shù)學(xué)總復(fù)習(xí) 第14講 一般三角形及其性質(zhì)》由會員分享，可在線閱讀，更多相關(guān)《陜西省山陽縣色河鋪鎮(zhèn)2018年中考數(shù)學(xué)總復(fù)習(xí) 第14講 一般三角形及其性質(zhì)（2頁珍藏版）》請在裝配圖網(wǎng)上搜索。
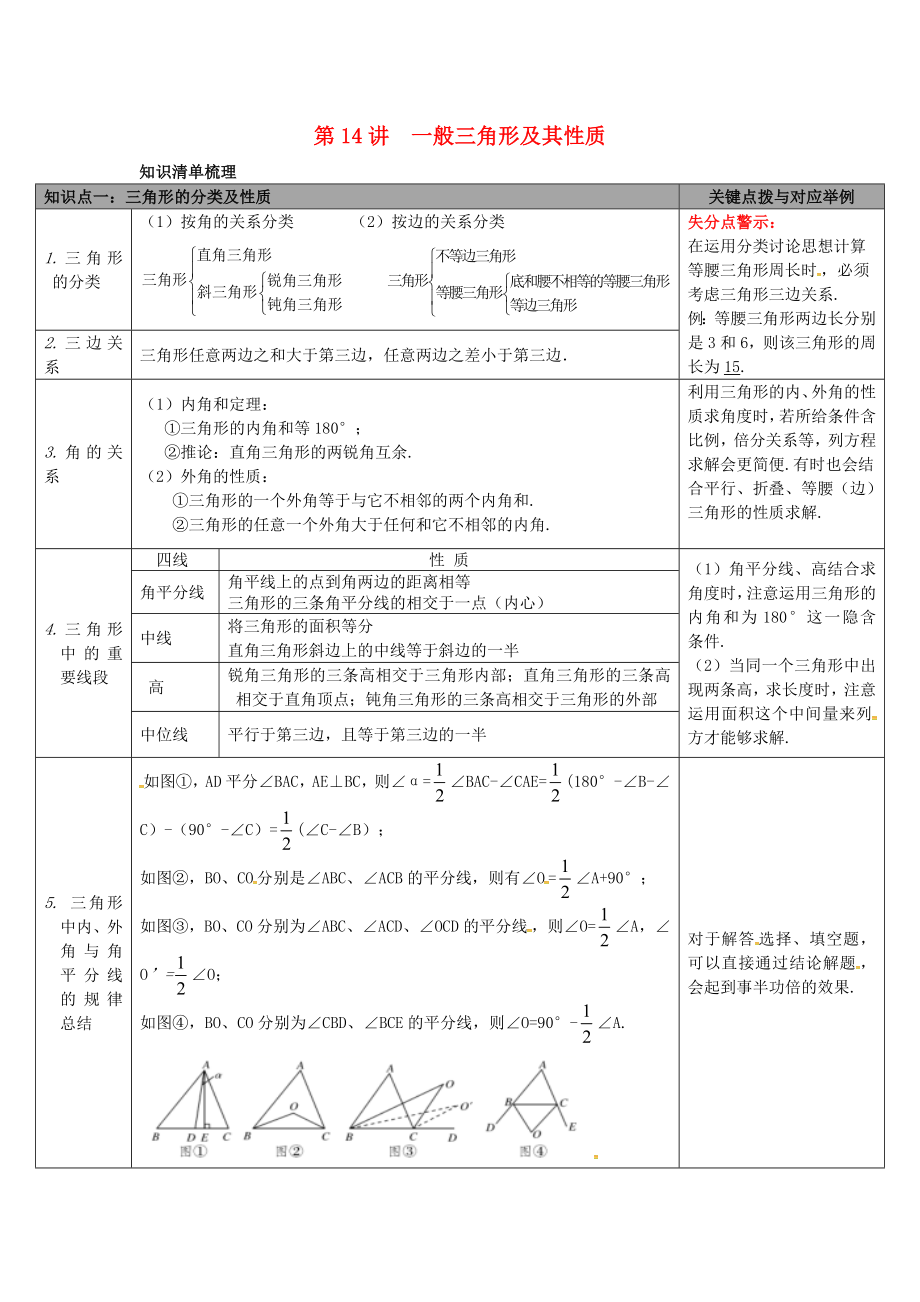
1、第14講 一般三角形及其性質(zhì)知識清單梳理知識點一：三角形的分類及性質(zhì) 關(guān)鍵點撥與對應(yīng)舉例1.三角形的分類（1）按角的關(guān)系分類 （2）按邊的關(guān)系分類 失分點警示：在運用分類討論思想計算等腰三角形周長時，必須考慮三角形三邊關(guān)系.例：等腰三角形兩邊長分別是3和6，則該三角形的周長為15.2.三邊關(guān)系三角形任意兩邊之和大于第三邊，任意兩邊之差小于第三邊3.角的關(guān)系（1）內(nèi)角和定理：三角形的內(nèi)角和等180； 推論：直角三角形的兩銳角互余.（2）外角的性質(zhì)：三角形的一個外角等于與它不相鄰的兩個內(nèi)角和.三角形的任意一個外角大于任何和它不相鄰的內(nèi)角.利用三角形的內(nèi)、外角的性質(zhì)求角度時，若所給條件含比例，倍分關(guān)
2、系等，列方程求解會更簡便.有時也會結(jié)合平行、折疊、等腰（邊）三角形的性質(zhì)求解.4.三角形中的重要線段四線性 質(zhì)（1）角平分線、高結(jié)合求角度時，注意運用三角形的內(nèi)角和為180這一隱含條件.（2）當(dāng)同一個三角形中出現(xiàn)兩條高，求長度時，注意運用面積這個中間量來列方才能夠求解.角平分線角平線上的點到角兩邊的距離相等三角形的三條角平分線的相交于一點（內(nèi)心）中線將三角形的面積等分直角三角形斜邊上的中線等于斜邊的一半 高銳角三角形的三條高相交于三角形內(nèi)部；直角三角形的三條高相交于直角頂點；鈍角三角形的三條高相交于三角形的外部中位線平行于第三邊，且等于第三邊的一半5. 三角形中內(nèi)、外角與角平分線的規(guī)律總結(jié)如圖
3、，AD平分BAC，AEBC，則=BAC-CAE=(180-B-C）-（90-C）=(C-B）；如圖，BO、CO分別是ABC、ACB的平分線，則有O=A+90；如圖，BO、CO分別為ABC、ACD、OCD的平分線，則O=A，O=O；如圖，BO、CO分別為CBD、BCE的平分線，則O=90-A.對于解答選擇、填空題，可以直接通過結(jié)論解題，會起到事半功倍的效果.知識點二 ：三角形全等的性質(zhì)與判定6.全等三角形的性質(zhì)(1)全等三角形的對應(yīng)邊、對應(yīng)角相等(2)全等三角形的對應(yīng)角平分線、對應(yīng)中線、對應(yīng)高相等(3)全等三角形的周長等、面積等失分點警示：運用全等三角形的性質(zhì)時，要注意找準(zhǔn)對應(yīng)邊與對應(yīng)角.7.三
4、角形全等的判定一般三角形全等SSS（三邊對應(yīng)相等）SAS（兩邊和它們的夾角對應(yīng)相等）ASA（兩角和它們的夾角對應(yīng)相等）AAS（兩角和其中一個角的對邊對應(yīng)相等）失分點警示如圖，SSA和AAA不能判定兩個三角形全等.直角三角形全等(1)斜邊和一條直角邊對應(yīng)相等（HL）(2)證明兩個直角三角形全等同樣可以用 SAS,ASA和AAS. 8.全等三角形的運用（1）利用全等證明角、邊相等或求線段長、求角度：將特征的邊或角放到兩個全等的三角形中，通過證明全等得到結(jié)論.在尋求全等的條件時，注意公共角、公共邊、對頂角等銀行條件.（2）全等三角形中的輔助線的作法：直接連接法：如圖，連接公共邊，構(gòu)造全等.倍長中線法：用于證明線段的不等關(guān)系，如圖，由SAS可得ACDEBD，則AC=BE.在ABE中，AB+BEAE，即AB+AC2AD.截長補短法：適合證明線段的和差關(guān)系，如圖、.例：如圖，在ABC中，已知1=2，BE=CD，AB=5，AE=2，則CE=3.典例講解內(nèi)參P56-2、4、5、6、7、10、11、12、14、16、18、20 P58-1、2、4、6、9、11、14、17、20 P61-4、5、6三、課后反思：
陜西省山陽縣色河鋪鎮(zhèn)2018年中考數(shù)學(xué)總復(fù)習(xí) 第14講 一般三角形及其性質(zhì)
