《人教版八年級數(shù)學(xué)上學(xué)期 第12章 全等三角形單元練習(xí)試題》由會員分享,可在線閱讀����,更多相關(guān)《人教版八年級數(shù)學(xué)上學(xué)期 第12章 全等三角形單元練習(xí)試題(8頁珍藏版)》請在裝配圖網(wǎng)上搜索。
1��、第12章 全等三角形
一.選擇題
1.下列說法正確的是( ?。?
A.形狀相同的兩個圖形一定全等
B.兩個長方形是全等圖形
C.兩個全等圖形面積一定相等
D.兩個正方形一定是全等圖形
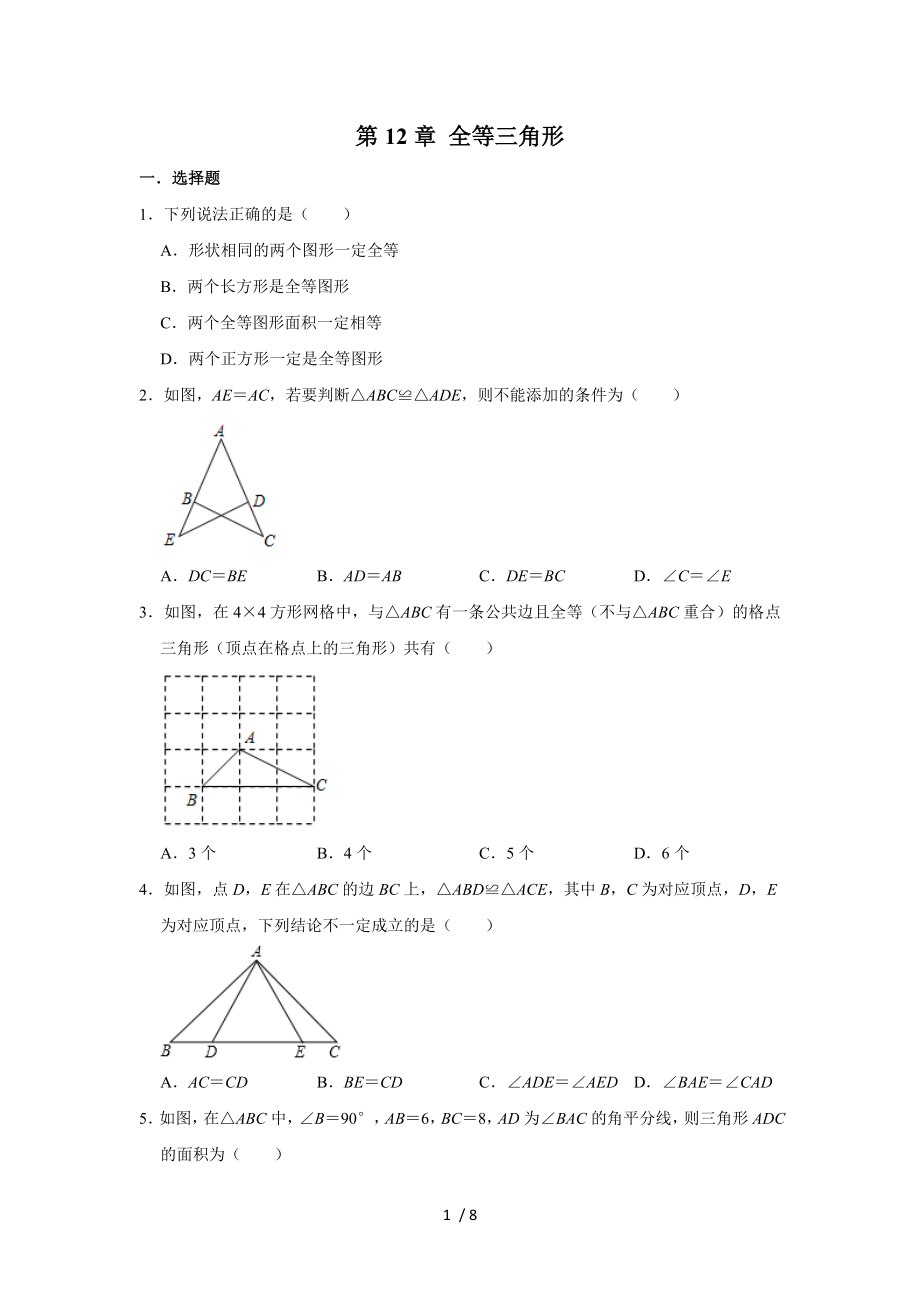
2.如圖����,AE=AC��,若要判斷△ABC≌△ADE,則不能添加的條件為( ?�。?
A.DC=BE B.AD=AB C.DE=BC D.∠C=∠E
3.如圖���,在4×4方形網(wǎng)格中�����,與△ABC有一條公共邊且全等(不與△ABC重合)的格點三角形(頂點在格點上的三角形)共有( ?。?
A.3個 B.4個 C.5個 D.6個
4.如圖,點D��,E在△ABC的邊BC上�����,△ABD≌△ACE����,其中B,C為
2�����、對應(yīng)頂點�����,D����,E為對應(yīng)頂點�����,下列結(jié)論不一定成立的是( ?。?
A.AC=CD B.BE=CD C.∠ADE=∠AED D.∠BAE=∠CAD
5.如圖,在△ABC中���,∠B=90°,AB=6�,BC=8�,AD為∠BAC的角平分線���,則三角形ADC的面積為( )
A.3 B.10 C.12 D.15
6.如圖���,點D���,E分別在線段AB�����,AC上���,CD與BE相交于O點��,已知AB=AC���,現(xiàn)添加以下的哪個條件仍無法判定△ABE≌△ACD的是( )
A.AD=AE B.∠B=∠C C.CD=BE D.∠ADC=∠AEB
7.如圖�����,在△ABC中���,AD⊥BC于點D��,BE⊥AC于點E���,AD與B
3�、E相交于點F�����,若BF=AC,∠CAD=25°�,則∠ABE的度數(shù)為( )
A.30° B.15° C.25° D.20°
8.如圖���,已知四邊形ABCD中��,AC平分∠BAD�����,AB=AC=5�,AD=3��,BC=CD.則點C到AB的距離是( )
A. B. C.3 D.2
9.如圖���,在Rt△ABC中���,∠C=90°,AD是∠BAC的平分線���,若AC=3�����,BC=4����,則S△ABD:S△ACD為( ?����。?
A.5:4 B.5:3 C.4:3 D.3:4
10.如圖���,△AOB的外角∠CAB�,∠DBA的平分線AP���,BP相交于點P�����,PE⊥OC于E����,PF⊥OD于F��,下列結(jié)論:(1)PE=PF��;(
4���、2)點P在∠COD的平分線上�;(3)∠APB=90°﹣∠O�����,其中正確的有( ?����。?
A.0個 B.1個 C.2個 D.3個
二.填空題
11.如圖中有6個條形方格圖,圖上由實線圍成的圖形與(1)是全等形的有 .
12.在如圖所示的3×3的正方形網(wǎng)格中��,∠1+∠2+∠3的度數(shù)為 .
13.如圖��,∠A=∠D��,∠1=∠2���,要得到△ABC≌△DEF,添加一個條件可以是 ?。?
14.如圖�,在方格紙中,以AB為一邊作△ABP����,使之與△ABC全等�,從P1,P2�����,P3��,P4���,四個點中��,滿足條件的點P有 個.
15.如圖�,在△ABC中,∠A=90°���,
5���、AB=AC�����,∠ABC的平分線BD交AC于點D�����,CE⊥BD����,交BD的延長線于點E,若BD=8,則CE= ?�。?
三.解答題
16.如圖所示����,已知△ABC≌△FED���,AF=8�,BE=2.
(1)求證:AC∥DF.
(2)求AB的長.
17.如圖,點B�,F(xiàn)����,C���,E在直線l上�����,點A�����,D在l異側(cè),AB=DE��,AB∥DE��,∠A=∠D.求證:△ABC≌△DEF.
18.如圖��,在△ABC中��,∠ACB=45°����,過點A作AD⊥BC于點D,點E為AD上一點�,且ED=BD.
(1)求證:△ABD≌△CED;
(2)若CE為∠ACD的角平分線,求∠BAC的度數(shù).
19.在△ABC中
6���、��,∠C=90°����,AD平分∠BAC交BC于點D,BD:DC=2:1����,BC=7.8cm�����,求點D到AB的距離.
20.如圖�����,沿AC方向開山修路����,為了加快施工進(jìn)度,要在山的另一面同時施工�����,工人師傅在AC上取一點B���,在小山外取一點D,連接BD并延長�����,使DF=BD,過F點作AB的平行線MF�����,連接MD并延長��,在延長線上取一點E��,使DE=DM�,在E點開工就能使A,C����,E成一條直線����,你知道其中的道理嗎����?
參考答案
一.選擇題
1. C.
2.C.
3. B.
4. A.
5. D.
6. C.
7. D.
8. C.
9. B.
10. C.
二.填空題(共5小題)
7、11.(2)��,(3)����,(6)����,
12. 135°
13. DF=AC或CD=AF.
14. 2.
15. 4.
三.解答題
16.證明:(1)∵△ABC≌△FED�����,
∴∠A=∠F.
∴AC∥DF.
(2)∵△ABC≌△FED�,
∴AB=EF.
∴AB﹣EB=EF﹣EB.
∴AE=BF.
∵AF=8��,BE=2
∴AE+BF=8﹣2=6
∴AE=3
∴AB=AE+BE=3+2=5
17.證明:∵AB∥DE(已知),
∴∠ABC=∠DEF(兩直線平行���,內(nèi)錯角相等)���,
在△ABC和△DEF中
∴△ABC≌△DEF(ASA).
18.(1)證明:∵AD⊥BC
8、���,∠ACB=45°���,
∴∠ADB=∠CDE=90°����,△ADC是等腰直角三角形,
∴AD=CD�,∠CAD=∠ACD=45°,
在△ABD與△CED中,,
∴△ABD≌△CED(SAS)�����;
(2)解:∵CE為∠ACD的角平分線�����,
∴∠ECD=∠ACD=22.5°,
由(1)得:△ABD≌△CED���,
∴∠BAD=∠ECD=22.5°,
∴∠BAC=∠BAD+∠CAD=22.5°+45°=67.5°.
19.解:過點D作DE⊥AB于E.
∵AD平分∠BAC��,DE⊥AB�����,DC⊥AC
∴CD=DE
又BD:DC=2:1,BC=7.8cm
∴DC=7.8÷(2+1)=7.8÷3=2.6cm.
∴DE=DC=2.6cm.
∴點D到AB的距離為2.6cm.
20.解:∵在△BDE和△FDM中����,
∴△BDE≌△FDM(SAS)��,
∴∠BEM=∠FME���,
∴BE∥MF���,
∵AB∥MF����,
∴A���、C�����、E三點在一條直線上.
8 / 8
 人教版八年級數(shù)學(xué)上學(xué)期 第12章 全等三角形單元練習(xí)試題
人教版八年級數(shù)學(xué)上學(xué)期 第12章 全等三角形單元練習(xí)試題