《2010高考數(shù)學(xué)導(dǎo)學(xué)練系列 復(fù)數(shù)教案 蘇教版》由會員分享�,可在線閱讀,更多相關(guān)《2010高考數(shù)學(xué)導(dǎo)學(xué)練系列 復(fù)數(shù)教案 蘇教版(9頁珍藏版)》請在裝配圖網(wǎng)上搜索�����。
1��、考綱導(dǎo)讀
數(shù)系的擴(kuò)充與復(fù)數(shù)的引入
1����、了解數(shù)系的擴(kuò)充過程��,體會實際需求與數(shù)學(xué)內(nèi)部的矛盾(數(shù)的運(yùn)算規(guī)則�����、方程理論)在數(shù)系擴(kuò)充過程中的作用.
2�、理解復(fù)數(shù)的基本概念以及復(fù)數(shù)相等的充要條件
3��、了解復(fù)數(shù)的代數(shù)表示法及其幾何意義��,能進(jìn)行復(fù)數(shù)代數(shù)形式的四則運(yùn)算�,了解復(fù)數(shù)代數(shù)形式的加、減運(yùn)算的幾何意義.
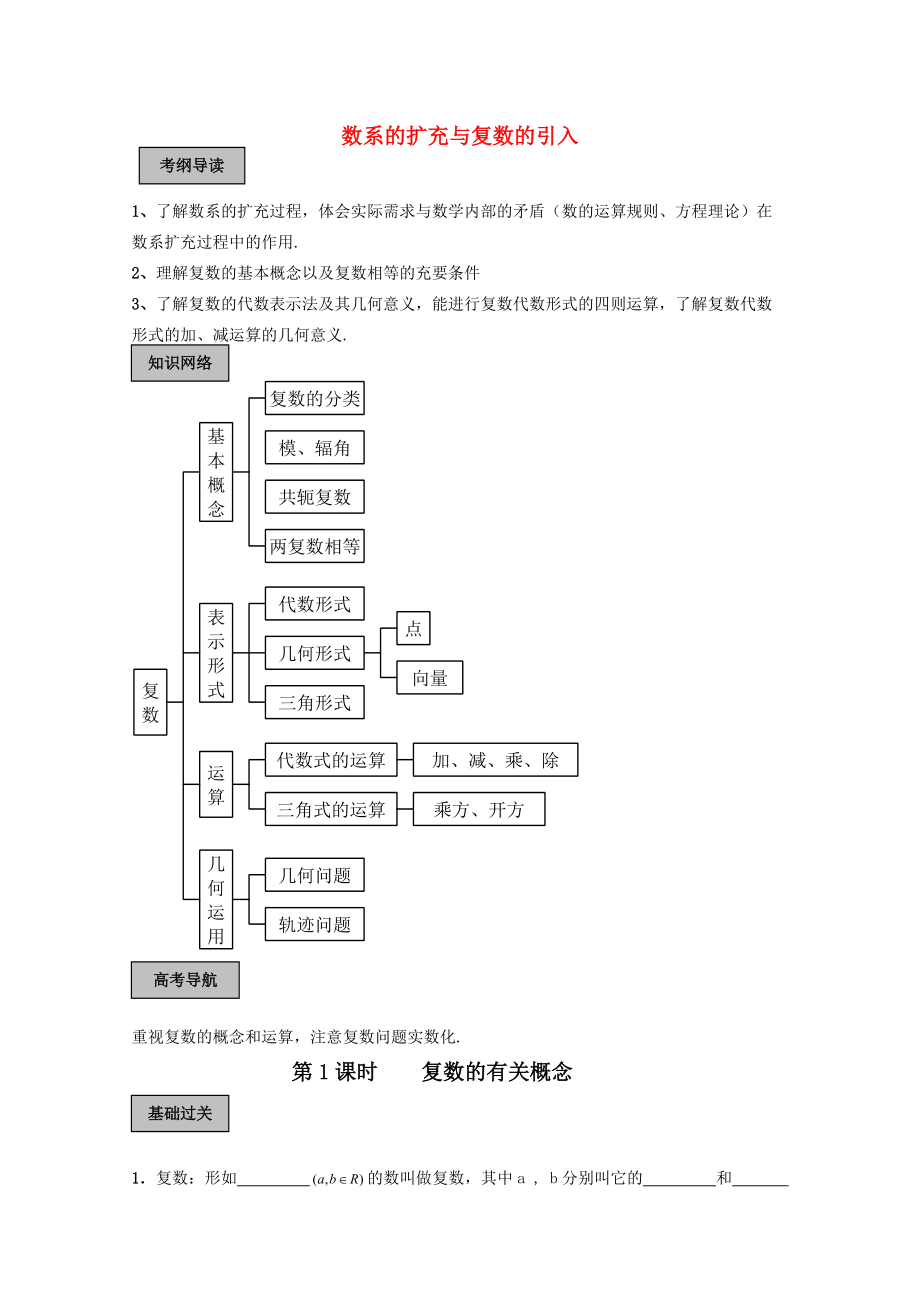
知識網(wǎng)絡(luò)
高考導(dǎo)航
重視復(fù)數(shù)的概念和運(yùn)算��,注意復(fù)數(shù)問題實數(shù)化.
第1課時 復(fù)數(shù)的有關(guān)概念
基礎(chǔ)過關(guān)
1.復(fù)數(shù):形如 的數(shù)叫做復(fù)數(shù)����,其中a , b分別叫它的 和 .
2.分類:設(shè)復(fù)數(shù):
(1) 當(dāng)
2、 =0時�����,z為實數(shù)��;
(2) 當(dāng) 0時,z為虛數(shù)�����;
(3) 當(dāng) =0, 且 0時�����,z為純虛數(shù).
3.復(fù)數(shù)相等:如果兩個復(fù)數(shù) 相等且 相等就說這兩個復(fù)數(shù)相等.
4.共軛復(fù)數(shù):當(dāng)兩個復(fù)數(shù)實部 ����,虛部 時.這兩個復(fù)數(shù)互為共軛復(fù)數(shù).(當(dāng)虛部不為零時��,也可說成互為共軛虛數(shù)).
5.若z=a+bi, (a, bR), 則 | z |= ����; z= .
6.復(fù)平面:建立直角坐標(biāo)系來表示復(fù)數(shù)的平面叫做復(fù)平面, x軸叫做 , 叫虛軸.
7.復(fù)數(shù)z
3�����、=a+bi(a, bR)與復(fù)平面上的點 建立了一一對應(yīng)的關(guān)系.
8.兩個實數(shù)可以比較大小�����、但兩個復(fù)數(shù)如果不全是實數(shù),就 比較它們的大小.
典型例題
例1. m取何實數(shù)值時,復(fù)數(shù)z=+是實數(shù)�?是純虛數(shù)?
解:① z是實數(shù)
② z為純虛數(shù)
變式訓(xùn)練1:當(dāng)m分別為何實數(shù)時�,復(fù)數(shù)z=m2-1+(m2+3m+2)i是(1)實數(shù)?(2)虛數(shù)����?(3)純虛數(shù)?(4)零��?
解:(1)m=-1,m=-2��;(2)m≠-1,m≠-2����;(3)m=1;(4)m=-1.
例2. 已知x����、y為共軛復(fù)數(shù),且��,求x.
解:設(shè)代入由復(fù)數(shù)相等的概念可得
變式訓(xùn)練2:已知復(fù)
4��、數(shù)z=1+i��,如果=1-i,求實數(shù)a,b的值.
由z=1+i得
==(a+2)-(a+b)i
從而,解得.
例3. 若方程至少有一個實根����,試求實數(shù)m的值.
解:設(shè)實根為,代入利用復(fù)數(shù)相等的概念可得=
變式訓(xùn)練3:若關(guān)于x 的方程x2+(t2+3t+tx )i=0有純虛數(shù)根�,求實數(shù)t的值和該方程的根.
解:t=-3,x1=0,x2=3i.提示:提示:設(shè)出方程的純虛數(shù)根,分別令實部�����、虛部為0�����,將問題轉(zhuǎn)化成解方程組.
例4. 復(fù)數(shù)滿足��,試求的最小值.
設(shè)�����,則����,
于是
變式訓(xùn)練4:已知復(fù)平面內(nèi)的點A�、B對應(yīng)的復(fù)數(shù)分別是、,其中��,設(shè)對應(yīng)的復(fù)數(shù)為.
(1) 求復(fù)數(shù)�����;
(2) 若復(fù)
5�����、數(shù)對應(yīng)的點P在直線上�����,求的值.
解:(1)
(2) 將代入
可得.
小結(jié)歸納
1.要理解和掌握復(fù)數(shù)為實數(shù)��、虛數(shù)��、純虛數(shù)��、零時�����,對實部和虛部的約束條件.
2.設(shè)z=a+bi (a�����,bR),利用復(fù)數(shù)相等和有關(guān)性質(zhì)將復(fù)數(shù)問題實數(shù)化是解決復(fù)數(shù)問題的常用方法.
第2課時 復(fù)數(shù)的代數(shù)形式及其運(yùn)算
基礎(chǔ)過關(guān)
1.復(fù)數(shù)的加�����、減�、乘、除運(yùn)算按以下法則進(jìn)行:
設(shè)�,則
(1) = ;
(2) = �����;
(3) = ( ).
2.幾個重要的結(jié)論:
⑴
⑵ = =
6��、 .
⑶ 若z為虛數(shù)����,則=
3.運(yùn)算律
⑴ = .
⑵ = .
⑶ = .
典型例題
例1.計算:
解:提示:利用
原式=0
變式訓(xùn)練1:求復(fù)數(shù)
(A) (B) (C) (D)
解: 故選C�����;
例2. 若����,求
解:提示:利用
原式=
變式訓(xùn)練2:已知復(fù)數(shù)z滿足z2+1=0�����,則(z6+i)(z6-i)= ▲ .
解:2
例3. 已知����,問是否存在復(fù)數(shù)z�,使其滿足(aR),如果存在�,求出z的值,如果不存在�,說明理由
解:提示:設(shè)利用復(fù)數(shù)相等的概念有
7、
變式訓(xùn)練3:若�,其中是虛數(shù)單位,則a+b=__________
解:3
例4. 證明:在復(fù)數(shù)范圍內(nèi)����,方程(為虛數(shù)單位)無解.
證明:原方程化簡為
設(shè) 、y∈R��,代入上述方程得
將(2)代入(1)�,整理得無實數(shù)解,∴原方程在復(fù)數(shù)范圍內(nèi)無解.
變式訓(xùn)練4:已知復(fù)數(shù)z1滿足(1+i)z�1=-1+5i����,z2=a-2-i��,其中i為虛數(shù)單位��,a∈R, 若<�,求a的取值范圍.
解:由題意得 z1==2+3i,
于是==,=.
小結(jié)歸納
由<��,得a2-8a+7<0�����,1
8�����、必須準(zhǔn)確熟練地掌握.
2.記住一些常用的結(jié)果�����,如的有關(guān)性質(zhì)等可簡化運(yùn)算步驟提高運(yùn)算速度.
3.復(fù)數(shù)的代數(shù)運(yùn)算與實數(shù)有密切聯(lián)系但又有區(qū)別�,在運(yùn)算中要特別注意實數(shù)范圍內(nèi)的運(yùn)算法則在復(fù)數(shù)范圍內(nèi)是否適用.
�復(fù)數(shù)章節(jié)測試題
一、選擇題
1.若復(fù)數(shù)(����,為虛數(shù)單位)是純虛數(shù),則實數(shù)的值為 ( )
A、-6 B����、13 C. D.
2.定義運(yùn)算,則符合條件的復(fù)數(shù)對應(yīng)的點在( )
A.第一象限�; B.第二象限; C.第三象限��; D.第四象限�;
3.若復(fù)數(shù)是純虛數(shù)(是虛數(shù)單位),則實數(shù)(
9�����、 )
A.-4����; B.4�; C.-1��; D.1��;
4.復(fù)數(shù)=( )
A.-I B.I C. 2-i D.-2+i
6.若復(fù)數(shù)在復(fù)平面上對應(yīng)的點位于第二象限����,則實數(shù)a的取值范圍是( )
A. B. C. D.
7.已知復(fù)數(shù)z滿足,則z=( )
(A) -1+ i (B) 1+i (C) 1-i (D) -1-i
8.若復(fù)數(shù)�����,且為純虛數(shù)��,則實數(shù)為 ( )
A.1 B.-1 C.1或-1
10��、 D.0
9.如果復(fù)數(shù)的實部和虛部相等�����,則實數(shù)等于( )
(A) (B) (C) (D)
10.若z是復(fù)數(shù)�,且,則的一個值為 ( )
A.1-2 B.1+2 C.2- D.2+
11.若復(fù)數(shù)為純虛數(shù)�,其中為虛數(shù)單位�,則=( )
A. B. C. D.
12.復(fù)數(shù)在復(fù)平面中所對應(yīng)的點到原點的距離為( )
A. B. C.1 D.
二����、填空
11��、題
13.設(shè)�����,a��,b∈R�,將一個骰子連續(xù)拋擲兩次,第一次得到的點數(shù)為a����,第二次得到的點數(shù)為b,則使復(fù)數(shù)z2為純虛數(shù)的概率為 .
14.設(shè)i為虛數(shù)單位�,則 .
15.若復(fù)數(shù)z滿足方程,則z= .
16..已知實數(shù)x�,y滿足條件,(為虛數(shù)單位)�,則的最小值是 .
17.復(fù)數(shù)z=,則|z|= .
18.虛數(shù)(x-2)+ y其中x、y均為實數(shù)��,當(dāng)此虛數(shù)的模為1時,的取值范圍是( )
A.[-�����,] B.∪(
C.[-����,] D.[-,0∪(0�,
19.已知
12、 (a>0)��,且復(fù)數(shù)的虛部減去它的實部所得的差等于�����,求復(fù)數(shù)的模.
20..復(fù)平面內(nèi)����,點、分別對應(yīng)復(fù)數(shù)����、,且��,,
��,若可以與任意實數(shù)比較大小����,求的值(O為坐標(biāo)原點).
復(fù)數(shù)章節(jié)測試題答案
一�����、選擇題
1. A 2.答案:A 3.答案:B
4.答案:B
6.答案:A
7.A
8.B
9.B
10.B
11.D
12.B
二��、填空題
13.
14.2i
15.
16.答案:
17.答案:
18. 答案:B ∵, 設(shè)k =,
則k為過圓(x-2)2 + y2 = 1上點及原點
82615205
的直線斜率�,作圖如下, k≤,
又∵y≠0 ,∴k≠0.由對稱性 選B.
【幫你歸納】本題考查復(fù)數(shù)的概念,以及轉(zhuǎn)化與化歸的數(shù)學(xué)思維能力,利用復(fù)數(shù)與解析幾何��、平面幾何之間的關(guān)系求解.虛數(shù)一詞又強(qiáng)調(diào)y≠0��,這一易錯點.
【誤區(qū)警示】本題屬于基礎(chǔ)題����,每步細(xì)心計算是求解本題的關(guān)鍵,否則將會遭遇“千里之堤�����,潰于蟻穴”之尷尬.
19.解:
20.解:依題意為實數(shù),可得
 2010高考數(shù)學(xué)導(dǎo)學(xué)練系列 復(fù)數(shù)教案 蘇教版
2010高考數(shù)學(xué)導(dǎo)學(xué)練系列 復(fù)數(shù)教案 蘇教版