九年級(jí)數(shù)學(xué)上冊(cè) 第一章 特殊平行四邊形 3 正方形的性質(zhì)與判定 認(rèn)識(shí)正方形素材 新版北師大版

《九年級(jí)數(shù)學(xué)上冊(cè) 第一章 特殊平行四邊形 3 正方形的性質(zhì)與判定 認(rèn)識(shí)正方形素材 新版北師大版》由會(huì)員分享，可在線(xiàn)閱讀，更多相關(guān)《九年級(jí)數(shù)學(xué)上冊(cè) 第一章 特殊平行四邊形 3 正方形的性質(zhì)與判定 認(rèn)識(shí)正方形素材 新版北師大版（5頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

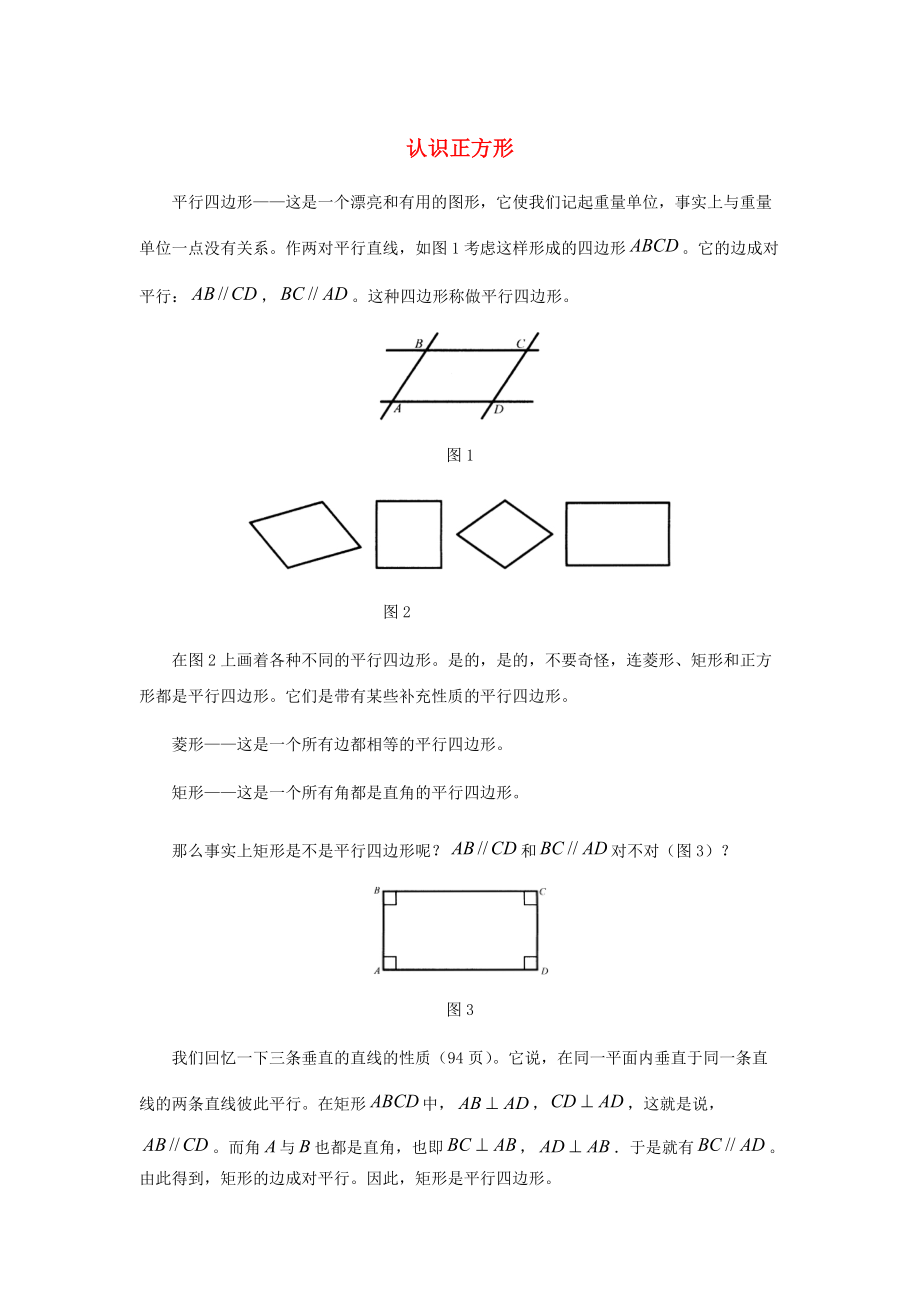
1、 認(rèn)識(shí)正方形 平行四邊形——這是一個(gè)漂亮和有用的圖形，它使我們記起重量單位，事實(shí)上與重量單位一點(diǎn)沒(méi)有關(guān)系。作兩對(duì)平行直線(xiàn)，如圖1考慮這樣形成的四邊形。它的邊成對(duì)平行：，。這種四邊形稱(chēng)做平行四邊形。 圖1 圖2 在圖2上畫(huà)著各種不同的平行四邊形。是的，是的，不要奇怪，連菱形、矩形和正方形都是平行四邊形。它們是帶有某些補(bǔ)充性質(zhì)的平行四邊形。 菱形——這是一個(gè)所有邊都相等的平行四邊形。 矩形——這是一個(gè)所有角都是直角的平行四邊形。 那么事實(shí)上矩形是不是平行四邊形呢？和對(duì)不對(duì)（圖3）？ 圖3 我們回憶一下三條垂直的直線(xiàn)的性質(zhì)（94頁(yè)）。它說(shuō)，在同一平面內(nèi)垂直于同一條直線(xiàn)

2、的兩條直線(xiàn)彼此平行。在矩形中，，，這就是說(shuō)，。而角與也都是直角，也即，．于是就有。由此得到，矩形的邊成對(duì)平行。因此，矩形是平行四邊形。 正方形是非常有趣的四邊形，能夠給它幾個(gè)定義。 1．正方形像菱形一樣，所有邊都相等，只是還要所有角都是直角。這就是說(shuō)，正方形是具有直角的菱形。 2．正方形像矩形一樣，所有角都是直角。只是還要所有邊都相等。這就是說(shuō)，正方形是所有邊都相等的矩形。 3．正方形像平行四邊形一樣，邊成對(duì)平行的。只是還要所有邊都相等和所有角都是直角。這就是說(shuō)，正方形是所有角都是直角和所有邊都相等的平行四邊形。 正方形還有一整套有趣的性質(zhì)。例如，如果要用給定長(zhǎng)度的籬笆圍住一個(gè)最大面

3、積的四邊形區(qū)域，那么應(yīng)當(dāng)把這區(qū)域選成正方形形狀。 用紙張的實(shí)驗(yàn)?zāi)軒椭覀兏玫貙W(xué)習(xí)平行線(xiàn)、垂線(xiàn)和平行四邊形。 用紙張的實(shí)驗(yàn) 在紙上標(biāo)明兩點(diǎn)和，隨后把紙對(duì)折，使得與重合。直線(xiàn)與折線(xiàn)相對(duì)位置是怎樣的？ 通過(guò)折一張紙，去得到一對(duì)平行直線(xiàn)和一對(duì)垂直直線(xiàn)。 從一張任意形狀的紙折疊并且隨后剪出一個(gè)矩形。指明在這矩形中哪些邊彼此平行或垂直。 剪切一個(gè)矩形，使其得到一個(gè)正方形。剪下這一正方形并研究它。通過(guò)正方形兩個(gè)相對(duì)頂點(diǎn)的折疊線(xiàn)稱(chēng)為正方形的對(duì)角錢(qián)。用折疊的方法可得到兩條對(duì)角錢(qián)。只用折疊紙的方法你們還能發(fā)現(xiàn)哪些性質(zhì)？記錄下這些性質(zhì)。 如果尋找這些性質(zhì)有困難，下面的研究計(jì)劃可能有幫助： 1．按長(zhǎng)

4、度比較兩條對(duì)角線(xiàn)。 2．兩條對(duì)角線(xiàn)之間相對(duì)位置怎樣？ 3．交點(diǎn)把對(duì)角線(xiàn)分成什么比例？ 4．每一條對(duì)角線(xiàn)把正方形分成什么樣的圖形？ 5．這些圖形是哪種類(lèi)型？ 6．對(duì)它們彼此之間進(jìn)行比較。 把正方形這樣對(duì)折，使它的兩條對(duì)邊重合。折疊線(xiàn)經(jīng)過(guò)哪些點(diǎn)？折疊線(xiàn)相對(duì)正方形各邊的位置怎樣？它把正方形分成什么樣的圖形？ 教師給孩子們一個(gè)任務(wù)，從一張彩色紙中剪出一個(gè)正方形。瓦夏剪出了一個(gè)正方形時(shí)，這樣檢驗(yàn)它：他比較了邊的長(zhǎng)度。全部4條邊發(fā)現(xiàn)是相等的，瓦夏就判定地完成了這個(gè)任務(wù)。這種檢驗(yàn)可信賴(lài)嗎？ 阿廖沙用另一種方法檢驗(yàn)了工作：他量的不是邊，而是對(duì)角線(xiàn)．對(duì)角線(xiàn)是相等的，阿廖沙就認(rèn)為正確地剪出了正方形

5、。這對(duì)嗎？ 萊娜剪了正方形后，比較了由對(duì)角線(xiàn)相互分成的所有4個(gè)線(xiàn)段。發(fā)現(xiàn)它們都是相等的。按照萊娜的意見(jiàn)，這證明了，剪出的四邊形是正方形。你們的意見(jiàn)怎樣？ 從一張紙剪出一個(gè)邊長(zhǎng)為和的矩形。從這矩形剪出一個(gè)邊長(zhǎng)為的正方形。余下一個(gè)邊長(zhǎng)為和的矩形，也就是一條邊同樣是另一條邊的大約1.6倍。隨后再?gòu)倪@矩形剪去一個(gè)邊長(zhǎng)為的正方形。余下的矩形，它的一條邊同樣是另一條邊的大約1.6倍。 這一過(guò)程可以繼續(xù)下去，對(duì)于進(jìn)之間的比近似1.6：l的矩形，很早以前就有人注意到了?？匆豢囱诺渑恋履凵駨R的造型（圖4）。甚至現(xiàn)在這還是世界最美麗的建筑之一，這神廟建筑于古希臘數(shù)學(xué)繁榮的年代，并且它的美麗就是建立在嚴(yán)格的數(shù)

6、學(xué)法則上的。如果我們?cè)谂恋履凵駨R周?chē)枰粋€(gè)矩形（圖5），那么發(fā)現(xiàn)，它的長(zhǎng)是寬的大約1.6倍，這種矩形稱(chēng)為黃金矩形。據(jù)說(shuō)，它的邊組成黃金分割。數(shù)學(xué)家給出了黃金分割的精確定義。 圖4 圖5 黃金分割——它將一個(gè)整體分割成兩個(gè)不相等的部分，使得大的部分對(duì)整體的比等于小的部分對(duì)大的部分的比。數(shù)1.6只是近似地（精確到0.1）表示黃金分割的值。 假如線(xiàn)段分成兩部分，小的部分長(zhǎng)度為，而大的部分長(zhǎng)度為（圖6），那么在黃金分割情況下。有趣的是， 圖6 在正五角星里，組成這一圖形的5條線(xiàn)中，每一條都把另外一條分成黃金分割的比（圖7）。 圖7 圖8中畫(huà)著一個(gè)貝殼：點(diǎn)分線(xiàn)段近似于黃金分割。 圖8 你看到過(guò)任何有黃金矩形形狀的物體嗎？ 按照?qǐng)D9中給出的指示，用圓規(guī)直尺作一個(gè)黃金矩形。 圖9 延長(zhǎng)底邊到與弧相交，在直角下作一側(cè)邊，這樣我們就完成黃金矩形的作圖。 我國(guó)經(jīng)濟(jì)發(fā)展進(jìn)入新常態(tài)，需要轉(zhuǎn)變經(jīng)濟(jì)發(fā)展方式，改變粗放式增長(zhǎng)模式，不斷優(yōu)化經(jīng)濟(jì)結(jié)構(gòu)，實(shí)現(xiàn)經(jīng)濟(jì)健康可持續(xù)發(fā)展進(jìn)區(qū)域協(xié)調(diào)發(fā)展，推進(jìn)新型城鎮(zhèn)化，推動(dòng)城鄉(xiāng)發(fā)展一體化因：我國(guó)經(jīng)濟(jì)發(fā)展還面臨區(qū)域發(fā)展不平衡、城鎮(zhèn)化水平不高、城鄉(xiāng)發(fā)展不平衡不協(xié)調(diào)等現(xiàn)實(shí)挑戰(zhàn)。