【冀教版】中考數(shù)學：知識清單梳理 第11講反比例函數(shù)的圖象和性質(zhì)

《【冀教版】中考數(shù)學：知識清單梳理 第11講反比例函數(shù)的圖象和性質(zhì)》由會員分享，可在線閱讀，更多相關(guān)《【冀教版】中考數(shù)學：知識清單梳理 第11講反比例函數(shù)的圖象和性質(zhì)（2頁珍藏版）》請在裝配圖網(wǎng)上搜索。

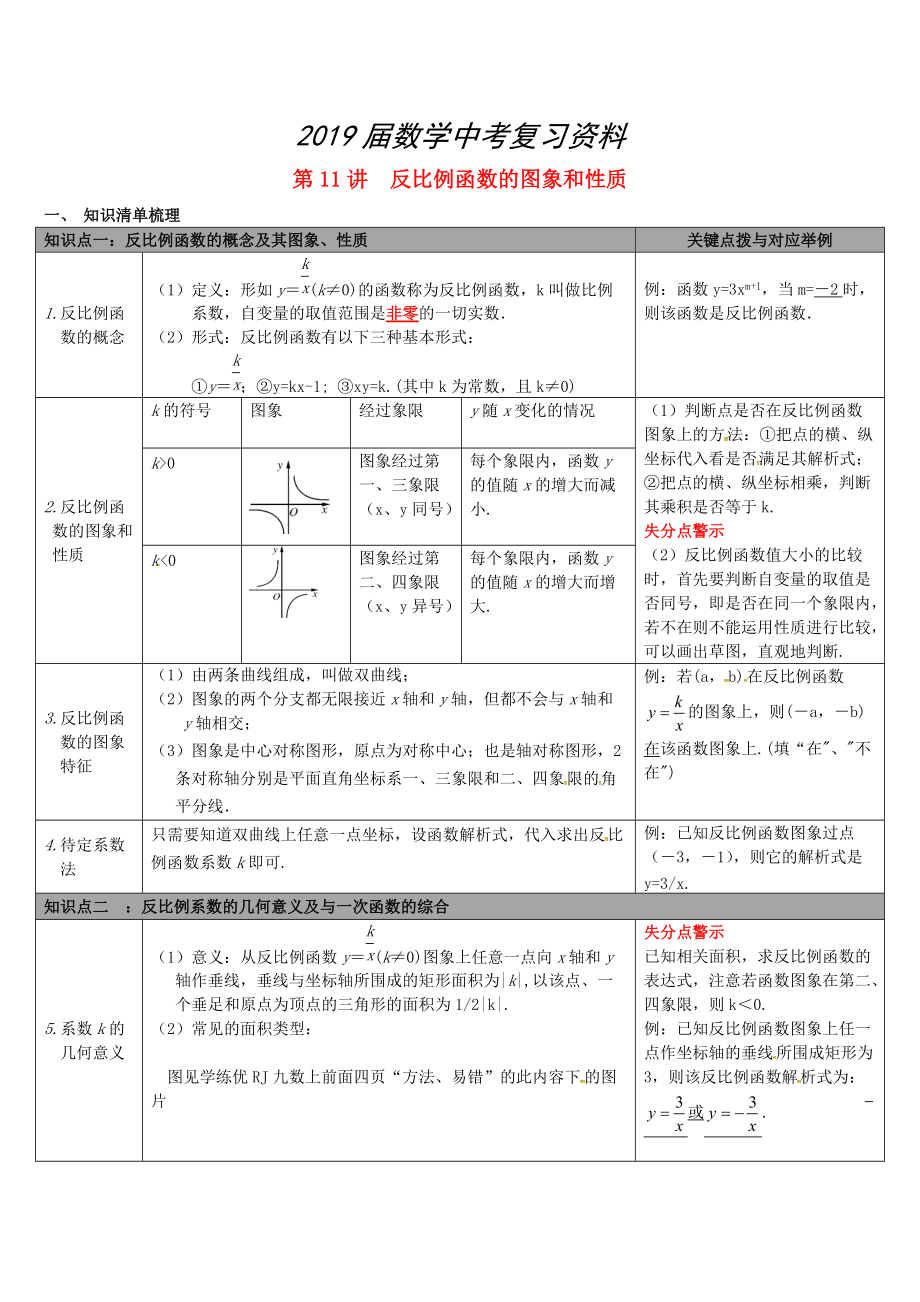
1、▼▼▼2019屆數(shù)學中考復習資料▼▼▼ 第11講 反比例函數(shù)的圖象和性質(zhì) 一、 知識清單梳理 知識點一：反比例函數(shù)的概念及其圖象、性質(zhì) 關(guān)鍵點撥與對應舉例 1.反比例函數(shù)的概念 （1）定義：形如y＝(k≠0)的函數(shù)稱為反比例函數(shù)，k叫做比例系數(shù)，自變量的取值范圍是非零的一切實數(shù)． （2）形式：反比例函數(shù)有以下三種基本形式： ①y＝；②y=kx-1; ③xy=k.(其中k為常數(shù)，且k≠0) 例：函數(shù)y=3xm+1，當m=－2時，則該函數(shù)是反比例函數(shù)． 2.反比例函數(shù)的圖象和性質(zhì) k的符號 圖象 經(jīng)過象限 y隨x變化的情況 （1）判斷點是否在

2、反比例函數(shù)圖象上的方法：①把點的橫、縱坐標代入看是否滿足其解析式；②把點的橫、縱坐標相乘，判斷其乘積是否等于k. 失分點警示 （2）反比例函數(shù)值大小的比較時，首先要判斷自變量的取值是否同號，即是否在同一個象限內(nèi)，若不在則不能運用性質(zhì)進行比較，可以畫出草圖，直觀地判斷. k>0 圖象經(jīng)過第一、三象限 （x、y同號） 每個象限內(nèi)，函數(shù)y的值隨x的增大而減小. k<0 圖象經(jīng)過第二、四象限 （x、y異號） 每個象限內(nèi)，函數(shù)y的值隨x的增大而增大. 3.反比例函數(shù)的圖象特征 （1）由兩條曲線組成，叫做雙曲線； （2）圖象的兩個分支都無限接近x軸和y軸，但都

3、不會與x軸和y軸相交； （3）圖象是中心對稱圖形，原點為對稱中心；也是軸對稱圖形，2條對稱軸分別是平面直角坐標系一、三象限和二、四象限的角平分線． 例：若(a，b)在反比例函數(shù)的圖象上，則(－a，－b)在該函數(shù)圖象上.(填“在"、"不在") 4.待定系數(shù)法 只需要知道雙曲線上任意一點坐標，設(shè)函數(shù)解析式，代入求出反比例函數(shù)系數(shù)k即可. 例：已知反比例函數(shù)圖象過點（－3，－1），則它的解析式是y=3/x. 知識點二 ：反比例系數(shù)的幾何意義及與一次函數(shù)的綜合 5.系數(shù)k的幾何意義 （1）意義：從反比例函數(shù)y＝(k≠0)圖象上任意一點向x軸和y軸作垂線，

4、垂線與坐標軸所圍成的矩形面積為|k|,以該點、一個垂足和原點為頂點的三角形的面積為1/2|k|. （2）常見的面積類型： 圖見學練優(yōu)RJ九數(shù)上前面四頁“方法、易錯”的此內(nèi)容下的圖片 失分點警示 已知相關(guān)面積，求反比例函數(shù)的表達式，注意若函數(shù)圖象在第二、四象限，則k＜0. 例：已知反比例函數(shù)圖象上任一點作坐標軸的垂線所圍成矩形為3，則該反比例函數(shù)解析式為： 或. 6.與一次函數(shù)的綜合 （1）確定交點坐標：【方法一】已知一個交點坐標為（a,b），則根據(jù)中心對稱性，可得另一個交點坐標為（-a,-b）.【方法二】聯(lián)立兩個函數(shù)解析式，利用方程思想求解. （2）確定函數(shù)

5、解析式：利用待定系數(shù)法，先確定交點坐標，再分別代入兩個函數(shù)解析式中求解 （3）在同一坐標系中判斷函數(shù)圖象：充分利用函數(shù)圖象與各字母系數(shù)的關(guān)系，可采用假設(shè)法，分k＞0和k＜0兩種情況討論，看哪個選項符合要求即可.也可逐一選項判斷、排除. （4）比較函數(shù)值的大?。褐饕ㄟ^觀察圖象，圖象在上方的值大，圖象在下方的值小，結(jié)合交點坐標，確定出解集的范圍. 涉及與面積有關(guān)的問題時，①要善于把點的橫、縱坐標轉(zhuǎn)化為圖形的邊長，對于不好直接求的面積往往可分割轉(zhuǎn)化為較好求的三角形面積；②也要注意系數(shù)k的幾何意義. 例：如圖所示，三個陰影部分的面積按從小到大的順序排列為：S△AOC=S△OPE＞S△BOD. 知識點三：反比例函數(shù)的實際應用 7 .一般步驟 （1題意找出自變量與因變量之間的乘積關(guān)系； （2設(shè)出函數(shù)表達式； （3）依題意求解函數(shù)表達式； （4）根據(jù)反比例函數(shù)的表達式或性質(zhì)解決相關(guān)問題.