安徽省長豐縣高中數(shù)學 第二章 圓錐曲線與方程 2.3.1 雙曲線及其標準方程教案 新人教A版選修11

《安徽省長豐縣高中數(shù)學 第二章 圓錐曲線與方程 2.3.1 雙曲線及其標準方程教案 新人教A版選修11》由會員分享，可在線閱讀，更多相關(guān)《安徽省長豐縣高中數(shù)學 第二章 圓錐曲線與方程 2.3.1 雙曲線及其標準方程教案 新人教A版選修11（5頁珍藏版）》請在裝配圖網(wǎng)上搜索。

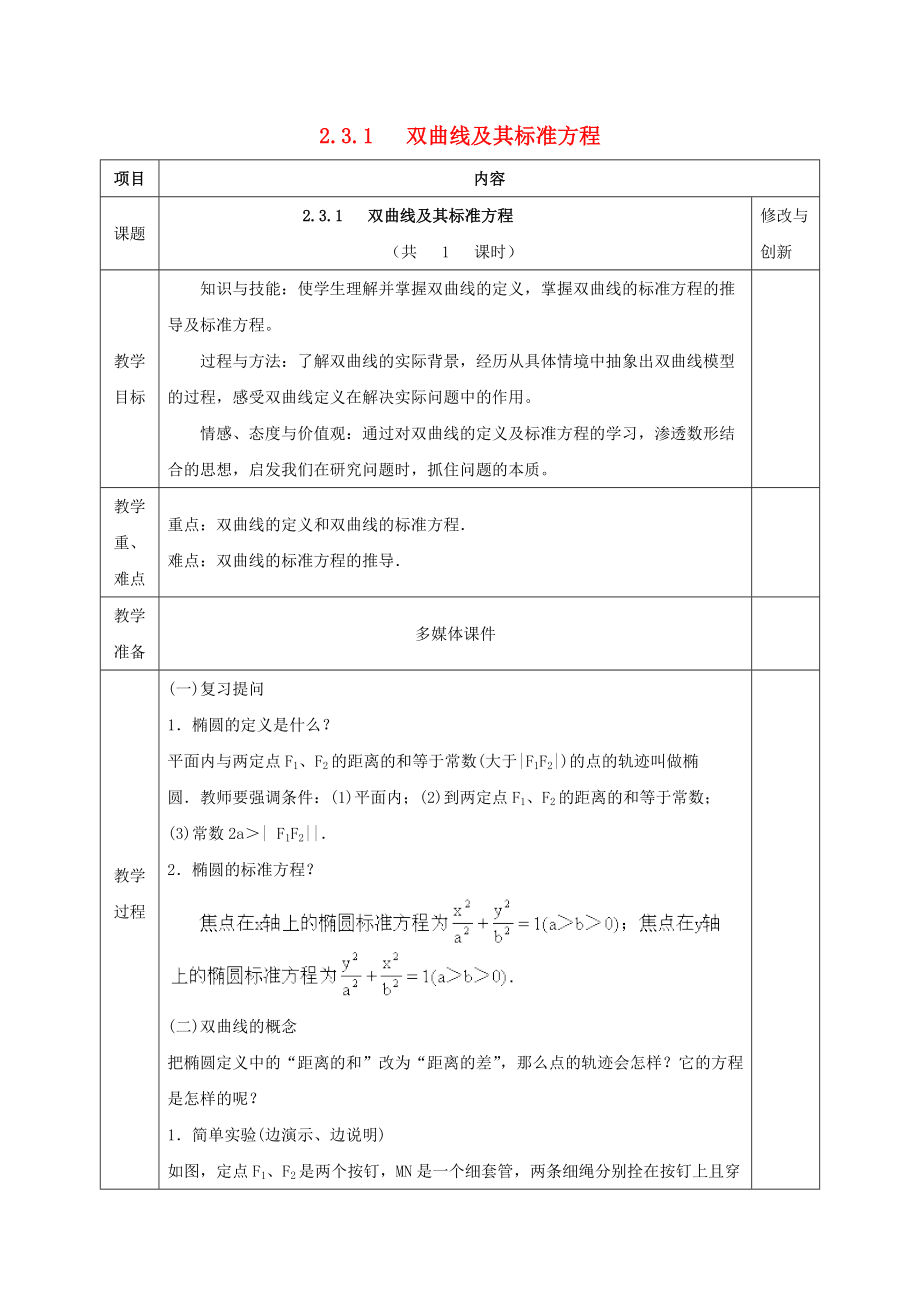
1、 2.3.1 雙曲線及其標準方程 項目 內(nèi)容 課題 2.3.1 雙曲線及其標準方程 （共 1 課時） 修改與創(chuàng)新 教學 目標 知識與技能：使學生理解并掌握雙曲線的定義，掌握雙曲線的標準方程的推導及標準方程。 過程與方法：了解雙曲線的實際背景，經(jīng)歷從具體情境中抽象出雙曲線模型的過程，感受雙曲線定義在解決實際問題中的作用。 情感、態(tài)度與價值觀：通過對雙曲線的定義及標準方程的學習，滲透數(shù)形結(jié)合的思想，啟發(fā)我們在研究問題時，抓住問題的本質(zhì)。 教學重、 難點 重點：雙曲線的定義和雙曲線的標準方程． 難點：雙曲線的標準方程的推導． 教學 準備

2、多媒體課件 教學過程 (一)復習提問 1．橢圓的定義是什么？ 平面內(nèi)與兩定點F1、F2的距離的和等于常數(shù)(大于|F1F2|)的點的軌跡叫做橢圓．教師要強調(diào)條件：(1)平面內(nèi)；(2)到兩定點F1、F2的距離的和等于常數(shù)；(3)常數(shù)2a＞| F1F2||． 2．橢圓的標準方程？ (二)雙曲線的概念 把橢圓定義中的“距離的和”改為“距離的差”，那么點的軌跡會怎樣？它的方程是怎樣的呢？ 1．簡單實驗(邊演示、邊說明) 如圖，定點F1、F2是兩個按釘，MN是一個細套管，兩條細繩分別拴在按釘上且穿過套管，點M移動時，|MF1|-|MF2|是常數(shù)，這樣就畫出曲線的一支；由|

3、MF2|-|MF1|是同一常數(shù)，可以畫出另一支． 注意：常數(shù)要小于| F1F2||，否則作不出圖形．這樣作出的曲線就叫做雙曲線． 2．設問 問題1：定點F1、F2與動點M不在平面上，能否得到雙曲線？ 請學生回答，不能．強調(diào)“在平面內(nèi)”． 問題2：|MF1|與|MF2|哪個大？ 請學生回答，不定：當M在雙曲線右支上時，|MF1|＞|MF2|；當點M在雙曲線左支上時，|MF1|＜|MF2|． 問題3：點M與定點F1、F2距離的差是否就是|MF1|-|MF2|？ 請學生回答，不一定，也可以是|MF2|-|MF1|．正確表示為||MF2|-|MF1||． 問題4：這個常數(shù)是否會大

4、于等于|F1F2|？ 請學生回答，應小于|F1F2|且大于零．當常數(shù)=|F1F2|時，軌跡是以F1、F2為端點的兩條射線；當常數(shù)＞|F1F2|時，無軌跡． 3．定義 在上述基礎(chǔ)上，引導學生概括雙曲線的定義： 平面內(nèi)與兩定點F1、F2的距離的差的絕對值是常數(shù)(小于|F1F2|)的點的軌跡叫做雙曲線．這兩個定點F1、F2叫做雙曲線的焦點，兩個焦點之間的距離叫做焦距． 教師指出：雙曲線的定義可以與橢圓相對照來記憶，不要死記． (三)雙曲線的標準方程 現(xiàn)在來研究雙曲線的方程．我們可以類似求橢圓的方程的方法來求雙曲線的方程．這時設問：求橢圓的方程的一般步驟方法是什么？不要求學生回答，主要引

5、起學生思考，隨即引導學生給出雙曲線的方程的推導． 標準方程的推導： (1)建系設點 取過焦點F1、F2的直線為x軸，線段F1F2的垂直平分線為y軸(如圖2-24) 建立直角坐標系． 設M(x，y)為雙曲線上任意一點，雙曲線的焦距是2c(c＞0)，那么F1、F2的坐標分別是(-c，0)、(c，0)．又設點M與F1、F2的距離的差的絕對值等于常數(shù)． (2)點的集合 由定義可知，雙曲線就是集合： P={M||MF1|-|MF2||=2a}={M|MF1|-|MF2|=2a}． (3)代數(shù)方程 (4)化簡方程(由學生演板) 將這個方程移項，兩邊平方得： 化簡整理得：

6、 (c2-a2)x2-a2y2=a2(c2-a2)． (以上推導完全可以仿照橢圓方程的推導．) 由雙曲線定義，2c＞2a　 即c＞a，所以c2-a2＞0． 設c2-a2=b2(b＞0)，代入上式得： b2x2-a2y2=a2b2． 這就是雙曲線的標準方程． 兩種標準方程的比較(引導學生歸納)： 說明： (1)雙曲線標準方程中，a＞0，b＞0，但a不一定大于b； (2)如果x2項的系數(shù)是正的，那么焦點在x軸上；如果y2項的系數(shù)是正的，那么焦點在y軸上．注意有別于橢圓通過比較分母的大小來判定焦點在哪一坐標軸上． (3)雙曲線標準方程中a、b、c的關(guān)系是c2=a2+

7、b2，不同于橢圓方程中c2=a2-b2． (四)例題講解： 1．求滿足下列的雙曲線的標準方程：焦點F1(-3，0)、F2(3，0)，且2a=4； 3．已知兩點F1(-5，0)、F2(5，0)，求與它們的距離的差的絕對值是6的點的軌跡方程．如果把這里的數(shù)字6改為12，其他條件不變，會出現(xiàn)什么情況？ 解：由定義，所求點的軌跡是雙曲線，因為c=5，a=3，所以b2=c2-a2=52-32=42． 因為2a=12，2c=10，且2a＞2c． 所以動點無軌跡． (五)課時小結(jié) 1．定義：平面內(nèi)與兩定點F1、F2的距離的差的絕對值等于常數(shù)(小于|F1F2|)的點的軌跡． 3．

8、圖形： 4．焦點：F1(-c，0)、F2(c，0)；F1(0，-c)、F2(0，c)． 5．a(chǎn)、b、c的關(guān)系：c2=a2+b2 五、布置作業(yè) 1．根據(jù)下列條件，求雙曲線的標準方程： (1)焦點的坐標是(-6，0)、(6，0)，并且經(jīng)過點A(-5，2)； 3．已知圓錐曲線的方程為mx2+ny2=m+n(m＜0＜m+n)，求其焦點坐標． 板書設計 2.3.1 雙曲線及其標準方程 1.雙曲線的定義 2. 雙曲線的標準方程 例 （1）焦點在x軸上 （2）焦點在y軸上 教學反思 1.為讓學生更深刻地理解雙曲線的定

9、義，在給出定義后，讓學生分析：平面內(nèi)到兩定點F1、F2的距離之和等于| F1F2|)的點的軌跡是什么？大于| F1F2|)的點的軌跡是什么？ 2.標準方程的推導，在老師的指導下，讓學生自己推導，以提高學生的運算能力。 6EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F375