高三數(shù)學(xué)一輪復(fù)習(xí)章節(jié)練習(xí)：39立體幾何與空間向量

《高三數(shù)學(xué)一輪復(fù)習(xí)章節(jié)練習(xí)：39立體幾何與空間向量》由會員分享，可在線閱讀，更多相關(guān)《高三數(shù)學(xué)一輪復(fù)習(xí)章節(jié)練習(xí)：39立體幾何與空間向量（9頁珍藏版）》請在裝配圖網(wǎng)上搜索。

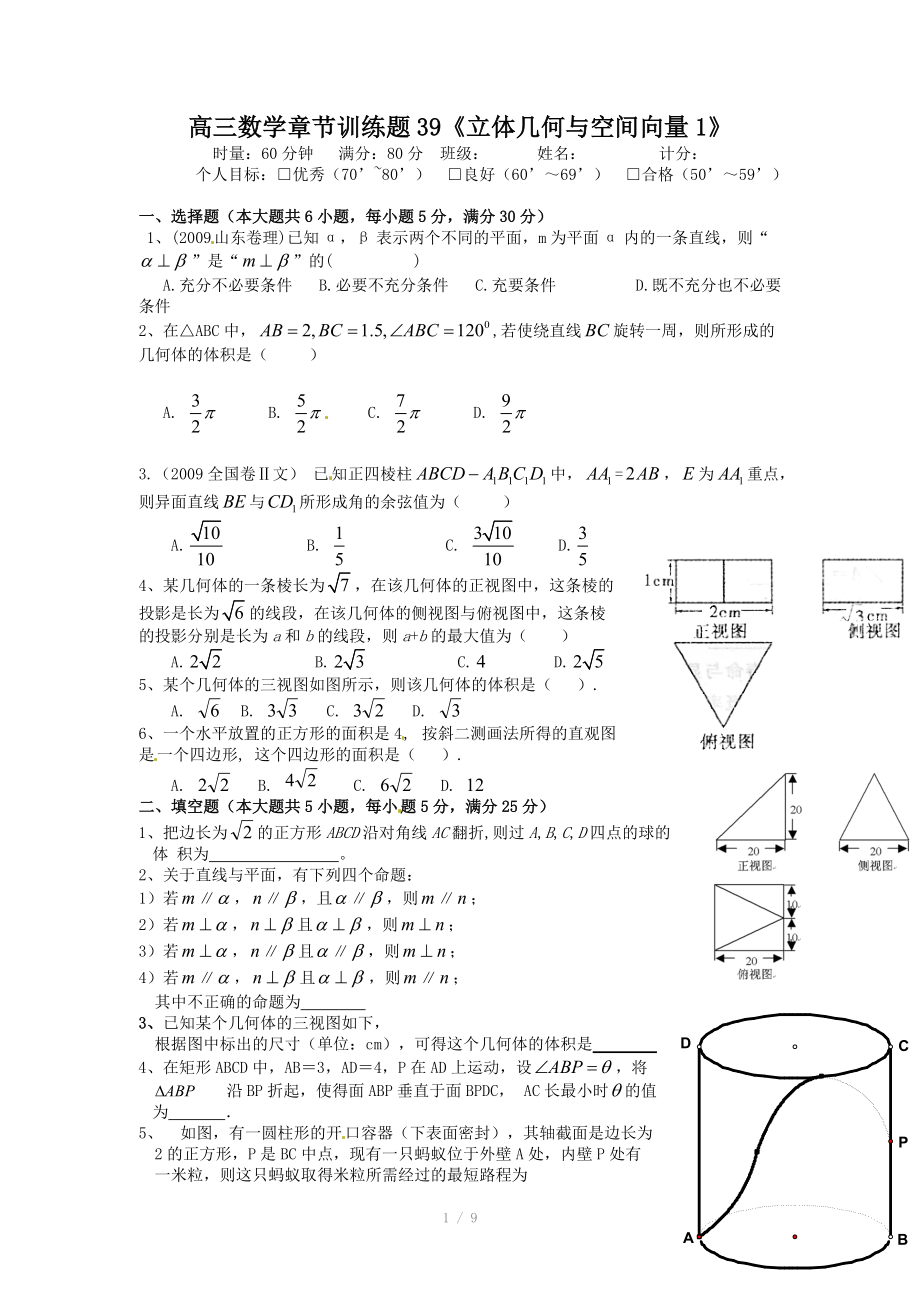
1、 高三數(shù)學(xué)章節(jié)訓(xùn)練題39《立體幾何與空間向量1》 時量：60分鐘 滿分：80分 班級： 姓名： 計分： 個人目標(biāo)：□優(yōu)秀（70’~80’） □良好（60’～69’） □合格（50’～59’） 一、選擇題（本大題共6小題，每小題5分，滿分30分） 1、(2009山東卷理)已知α，β表示兩個不同的平面，m為平面α內(nèi)的一條直線，則“”是“”的( ) A.充分不必要條件 B.必要不充分條件 C.充要條件 D.既不充分也不必要條件 2、在△ABC中，,若使繞直線旋轉(zhuǎn)一周，則所形成的幾何體的體積是（

2、 ） A. B. C. D. 3.（2009全國卷Ⅱ文） 已知正四棱柱中，=，為重點，則異面直線與所形成角的余弦值為（ ） A. B. C. D. 4、某幾何體的一條棱長為，在該幾何體的正視圖中，這條棱的投影是長為的線段，在該幾何體的側(cè)視圖與俯視圖中，這條棱的投影分別是長為a和b的線段，則a+b的最大值為（ ） A.　 B. 　C.　 D. 5、某個幾何體的三視圖如圖所示，則該幾何體的體積是（ ）. A. B.

3、 C. D. 6、一個水平放置的正方形的面積是4, 按斜二測畫法所得的直觀圖是一個四邊形, 這個四邊形的面積是（ ）. A. B. C. D. 二、填空題（本大題共5小題，每小題5分，滿分25分） 1、把邊長為的正方形ABCD沿對角線AC翻折,則過A,B,C,D四點的球的體 積為 。 2、關(guān)于直線與平面，有下列四個命題： 1）若∥，∥，且∥，則∥； 2）若，且，則； 3）若，∥且∥，則； 4）若∥，且，則∥； 其中不正確的命題為 3、已知某個幾何體的三視圖如下， 根據(jù)圖中標(biāo)出的尺寸（單

4、位：cm），可得這個幾何體的體積是 4、在矩形ABCD中，AB＝3，AD＝4，P在AD上運動，設(shè)，將 沿BP折起，使得面ABP垂直于面BPDC， AC長最小時的值為 ． 5、 如圖，有一圓柱形的開口容器（下表面密封），其軸截面是邊長為2的正方形，P是BC中點，現(xiàn)有一只螞蟻位于外壁A處，內(nèi)壁P處有一米粒，則這只螞蟻取得米粒所需經(jīng)過的最短路程為 1 / 9 。 三、解答題：（本大題共2小題，滿分25分） A B C A1 B1 C1 1、（2009廣東東莞

5、）在直三棱柱中，，，且異面直線與所成的角等于，設(shè).（1）求的值；（2）求平面與平面所成的銳二面角的大小. 2. 如圖，在三棱錐中，，，． （Ⅰ）求證：；（Ⅱ）求二面角的余弦值；（Ⅲ）求點到平面的距離． A C B D P 一、選擇題 1、【答案】:B【解析】:由平面與平面垂直的判定定理知如果m為平面α內(nèi)的 一條直線,,則,反過來則不一定.所以“”是“”的必要不充分條件. 2、【答案】.A

6、【解析】： 3.【答案】：C【解析】：本題考查異面直線夾角求法，方法一：利用平移，CD’∥BA,因此求△EBA中∠ABE即可，易知EB=,AE=1,AB=,故由余弦定理求cos∠ABE=，或由向量法可求。 4、【答案】C【解析】：結(jié)合長方體的對角線在三個面的投影來理解計算。如圖設(shè)長方體的高寬高分別為，由題意得， ，，所以， 當(dāng)且僅當(dāng)時取等號 5、【答案】D 【解析】從三視圖可以觀察發(fā)現(xiàn)幾何體是正三棱柱，底面邊長為2cm，高為1cm，所以體積為. 6、【答案】B 二、填空題 1、【解析】本題不告知翻折的角度，意在提醒學(xué)生找不變量。不難發(fā)現(xiàn)正方形對角線交點到四個頂點的距離相等，故交

7、點即為球心，半徑為1。 【答案】 2、【答案】1），4）； 【解析】 傳統(tǒng)空間位置關(guān)系的判斷依然是高考小題考查的重點，解決此類問題，可多參考教室空間，或手中的筆與桌子這些具體模型。 3、【解析】 三視圖是新增考點，根據(jù)三張圖的關(guān)系，可知幾何體是正方體的一部分，是一個四棱錐。本題也可改編為求該幾何體的外接球的表面積，則必須補全為正方體，增加了難度。 【答案】 4、【解析】本題是立體幾何中的最值問題，建立數(shù)學(xué)模型，用函數(shù)解決是一種重要方法。過A作AHBP于H，連CH， ∴．∴． 在， ∴在，，∴時，AC長最?。? 【答案】 5、 【解析】此類求曲面上最短路程問題通常

8、考慮側(cè)面展開。側(cè)面展開后得矩形，其中問題轉(zhuǎn)化為在上找一點使最短作關(guān)于的對稱點，連接，令與交于點則得 的最小值為 【答案】 三、填空題 解法一：（1）， 就是異面直線與所成的角， 即，……（2分） 連接，又，則 為等邊三角形，……………………………4分 由，， ；………6分 （2）取的中點，連接，過作于，連接， ,平面 ………………8分 又，所以平面，即， 所以就是平面與平面所成的銳二面角的平面角。…………10分 在中，，，, ，…………………………13分 因此平面與平面所成的銳二面角的大小為。…………1

9、4分 說明：取的中點，連接，…………同樣給分（也給10分） 解法二：（1）建立如圖坐標(biāo)系，于是，，，（） A1 B C B1 C1 x y z ，， …………3分 由于異面直線與所成的角， 所以與的夾角為 即 ………6分 （2）設(shè)向量且平面 于是且，即且， 又，，所以，不妨設(shè)……8分 同理得，使平面，（10分） 設(shè)與的夾角為，所以依， ，………………12分 平面，平面， 因此平面與平面所成的銳二面角的大小為?！?4分 說明：或者取的中點，連接，于是顯然平面 2. 解法一：（Ⅰ）取中點，連結(jié)．，．，．

10、，平面．平面，． （Ⅱ），，．又，． 又，即，且，平面．取中點．連結(jié)． A C B E P A C B D P H ，．是在平面內(nèi)的射影，． 是二面角的平面角．在中，，，，． （Ⅲ）由（Ⅰ）知平面，平面平面．過作，垂足為． 平面平面，平面．的長即為點到平面的距離． 由（Ⅰ）知，又，且，平面．平面，．在中，，， ．． 點到平面的距離為． 網(wǎng)解法二：（Ⅰ），，．又， ．，平面．平面，． （Ⅱ）如圖，以為原點建立空間直角坐標(biāo)系．則． 設(shè)．，，．取中點，連結(jié)． ，，，．是二面角的平面角． ，，， A C B P z x y H E ． （Ⅲ），在平面內(nèi)的射影為正的中心，且的長為點到平面的距離． 如（Ⅱ）建立空間直角坐標(biāo)系．，點的坐標(biāo)為．．中學(xué)學(xué)點到平面的距離為． 希望對大家有所幫助，多謝您的瀏覽！