陜西省吳堡縣吳堡中學(xué)高中數(shù)學(xué) 第一章 統(tǒng)計(jì)案例 獨(dú)立性檢驗(yàn)的步驟及應(yīng)用素材 北師大版選修

《陜西省吳堡縣吳堡中學(xué)高中數(shù)學(xué) 第一章 統(tǒng)計(jì)案例 獨(dú)立性檢驗(yàn)的步驟及應(yīng)用素材 北師大版選修》由會(huì)員分享，可在線閱讀，更多相關(guān)《陜西省吳堡縣吳堡中學(xué)高中數(shù)學(xué) 第一章 統(tǒng)計(jì)案例 獨(dú)立性檢驗(yàn)的步驟及應(yīng)用素材 北師大版選修（3頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

1、 獨(dú)立性檢驗(yàn)的步驟及應(yīng)用 一、 獨(dú)立性檢驗(yàn)的思想及步驟 獨(dú)立性檢驗(yàn)的基本思想類(lèi)似于數(shù)學(xué)上的“反證法”。要確認(rèn)“兩個(gè)分類(lèi)變量有關(guān)系”這一結(jié)論成立的可信程度。首先假設(shè)結(jié)論不成立，即“這兩個(gè)分類(lèi)變量幾乎沒(méi)有關(guān)系”（“幾乎獨(dú)立”）成立，則， 此時(shí)，我們所構(gòu)造的隨機(jī)變量應(yīng)該很小。如果由觀測(cè)數(shù)據(jù)計(jì)算得到的k不是很小，則在一定程度上說(shuō)明假設(shè)不合理。而且觀測(cè)值k越大，說(shuō)明假設(shè)（“幾乎無(wú)關(guān)或獨(dú)立”）不成立的可能性就越大，即兩者有關(guān)的可能性越大，這樣我們就可以由的觀測(cè)值k并結(jié)合已往估算經(jīng)驗(yàn)值表定出我們有多大程度等等把握可以認(rèn)為“兩個(gè)分類(lèi)變量有關(guān)系”。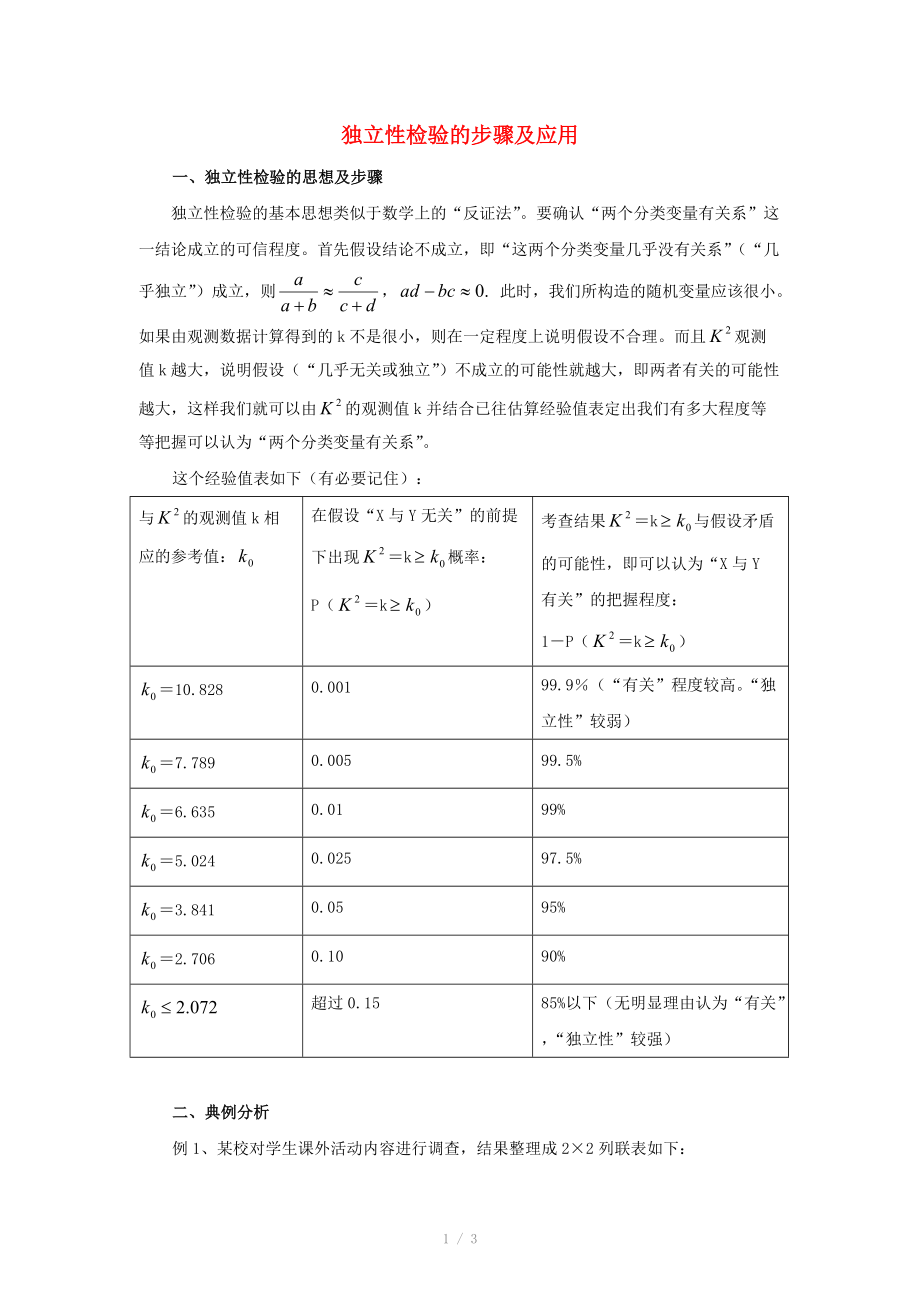 這個(gè)經(jīng)驗(yàn)值表如下（有必要記住）： 與的觀測(cè)值k相應(yīng)的

2、參考值： 在假設(shè)“X與Y無(wú)關(guān)”的前提下出現(xiàn)＝k概率： P（＝k） 考查結(jié)果＝k與假設(shè)矛盾的可能性，即可以認(rèn)為“X與Y有關(guān)”的把握程度： 1－P（＝k） ＝10.828 0.001 99.9％（“有關(guān)”程度較高?！蔼?dú)立性”較弱） ＝7.789 0.005 99.5% ＝6.635 0.01 99% ＝5.024 0.025 97.5% ＝3.841 0.05 95% ＝2.706 0.10 90% 超過(guò)0.15 85%以下（無(wú)明顯理由認(rèn)為“有關(guān)”，“獨(dú)立性”較強(qiáng)） 二、 典例分析 例1、某校對(duì)學(xué)生課外活動(dòng)內(nèi)容進(jìn)行調(diào)查，結(jié)果整理成22列聯(lián)

3、表如下： 1 / 3 體育 文娛 合計(jì) 男生 21 23 44 女生 6 29 35 合計(jì) 27 52 79 試分析“喜歡體育還是喜歡文娛”與“性別”之間三多大程度上有關(guān)？ 解：將a＝21，b＝23，c＝6，d＝29，n＝79代入， 得 即的觀察值 假設(shè)喜歡體育還是喜歡文娛與性別沒(méi)有關(guān)系，則的觀察值k應(yīng)該很小，且由經(jīng)驗(yàn)值表知，即在此假設(shè)成立的前提下出現(xiàn)的可能性只有0.005左右，而不出現(xiàn)的可能性約為99.5%，但在本調(diào)查中卻得出的觀察值 ，超過(guò)了7.789，所以我們有99.5％的把握可以認(rèn)為此假設(shè)不成立，即有99.5%的把握可以認(rèn)為喜歡體育還是

4、喜歡文娛與性別有關(guān)。 例2、調(diào)查在2～3級(jí)風(fēng)時(shí)的海上航行中男女乘客的暈船情況，共調(diào)查了71人，其中女性34人，男性37人。女性中有10人暈船，另外24人不暈船；男性中有12人暈船，另外25人不暈船。 （1） 根據(jù)以上數(shù)據(jù)建立有關(guān)22的列聯(lián)表； （2） 判斷暈船是否與性別有關(guān)系。 解：（1）22的列聯(lián)表： 暈船情況 性別 暈船 不暈船 總計(jì) 女 10 24 34 男 12 25 37 總計(jì) 22 49 71 （2）計(jì)算 因?yàn)閗<2.706，所以我們沒(méi)有理由說(shuō)“暈船與性別有關(guān)”。 例3、為了考查某種藥物預(yù)防疾病的效果，進(jìn)行動(dòng)物實(shí)驗(yàn)，得到如下的列聯(lián)表： 患病 未患病 總計(jì) 服用藥 10 45 55 沒(méi)服用藥 20 30 50 總計(jì) 30 75 105 請(qǐng)問(wèn)有多大把握認(rèn)為藥物有效？ 分析：本題考查回歸的基本思想、方法及初步應(yīng)用，會(huì)用殘差分析判斷回歸模型的擬合效果。 解：， 因?yàn)?，從而?7.5%的把握認(rèn)為藥物有效。 希望對(duì)大家有所幫助，多謝您的瀏覽！