《一元二次方程的概念預(yù)導(dǎo)學(xué)案九年級(jí)參考模版修改1》由會(huì)員分享�����,可在線閱讀,更多相關(guān)《一元二次方程的概念預(yù)導(dǎo)學(xué)案九年級(jí)參考模版修改1(3頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索����。
1���、九年級(jí)數(shù)學(xué)組“自主導(dǎo)學(xué)”研究資料
《一元二次方程的概念》預(yù)、導(dǎo)學(xué)案
設(shè)計(jì): 使用時(shí)間:第 周星期 總第 1 課時(shí)
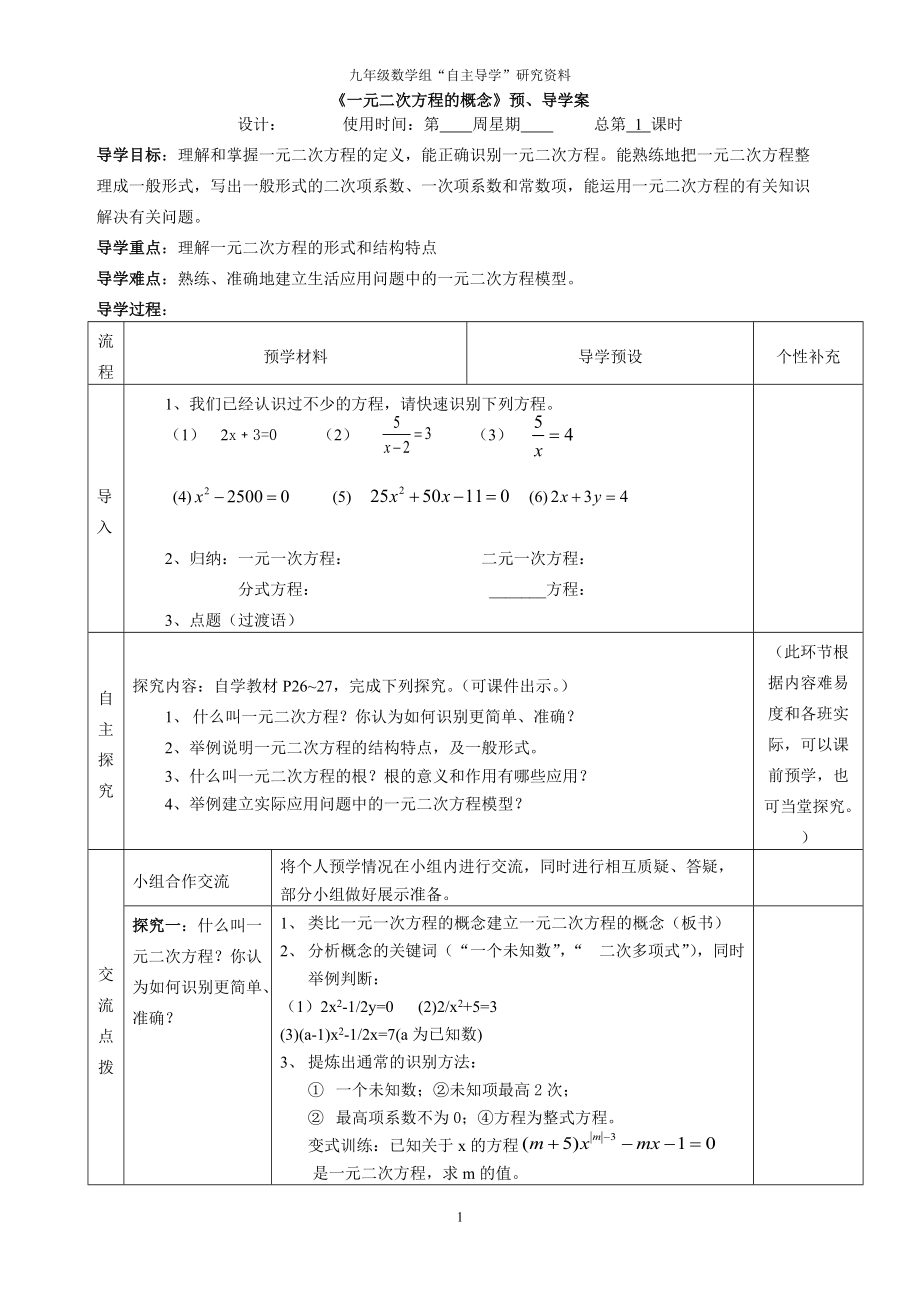
導(dǎo)學(xué)目標(biāo):理解和掌握一元二次方程的定義��,能正確識(shí)別一元二次方程��。能熟練地把一元二次方程整理成一般形式����,寫(xiě)出一般形式的二次項(xiàng)系數(shù)、一次項(xiàng)系數(shù)和常數(shù)項(xiàng)����,能運(yùn)用一元二次方程的有關(guān)知識(shí)解決有關(guān)問(wèn)題。
導(dǎo)學(xué)重點(diǎn):理解一元二次方程的形式和結(jié)構(gòu)特點(diǎn)
導(dǎo)學(xué)難點(diǎn):熟練�����、準(zhǔn)確地建立生活應(yīng)用問(wèn)題中的一元二次方程模型����。
導(dǎo)學(xué)過(guò)程:
流程
預(yù)學(xué)材料
導(dǎo)學(xué)預(yù)設(shè)
個(gè)性補(bǔ)充
導(dǎo)入
1、我們已經(jīng)認(rèn)識(shí)過(guò)不少的方程��,請(qǐng)快速識(shí)別下列方程�����。
(1) 2x﹢3=0
2、 (2) (3)
(4) (5) (6)
2����、歸納:一元一次方程: 二元一次方程:
分式方程: _______方程:
3、點(diǎn)題(過(guò)渡語(yǔ))
自主探究
探究?jī)?nèi)容:自學(xué)教材P26~27��,完成下列探究�����。(可課件出示���。)
1��、 什么叫一元二次方程����?你認(rèn)為如何識(shí)別更簡(jiǎn)單�����、準(zhǔn)確���?
2�����、舉例說(shuō)明一元二次方程的結(jié)構(gòu)特點(diǎn)��,及一般形式���。
3、什么叫一元二次方程的根����?根的意義和作用有哪些應(yīng)用?
4�、舉例建立實(shí)際應(yīng)用問(wèn)題中的一元二次方程模型?
(此環(huán)節(jié)根據(jù)內(nèi)容難易度
3��、和各班實(shí)際�,可以課前預(yù)學(xué),也可當(dāng)堂探究��。)
交流點(diǎn)撥
小組合作交流
將個(gè)人預(yù)學(xué)情況在小組內(nèi)進(jìn)行交流��,同時(shí)進(jìn)行相互質(zhì)疑、答疑�,部分小組做好展示準(zhǔn)備。
探究一:什么叫一元二次方程�����?你認(rèn)為如何識(shí)別更簡(jiǎn)單���、準(zhǔn)確�����?
1�����、 類比一元一次方程的概念建立一元二次方程的概念(板書(shū))
2���、 分析概念的關(guān)鍵詞(“一個(gè)未知數(shù)”,“ 二次多項(xiàng)式”)���,同時(shí)舉例判斷:
(1)2x2-1/2y=0 (2)2/x2+5=3
(3)(a-1)x2-1/2x=7(a為已知數(shù))
3���、 提煉出通常的識(shí)別方法:
① 一個(gè)未知數(shù);②未知項(xiàng)最高2次;
② 最高項(xiàng)系數(shù)不為0�;④方程為整式方程�����。
變式訓(xùn)練:已知關(guān)
4�����、于x的方程
是一元二次方程��,求m的值��。
分析:緊扣一元二次方程的定義����,必須滿足:二次項(xiàng)系數(shù)不為0,未知數(shù)的最高次數(shù)為2���。
探究二:舉例說(shuō)明一元二次方程的結(jié)構(gòu)特點(diǎn)���,及一般形式。
1���、從概念中明確其結(jié)構(gòu)特點(diǎn):左邊為二次多項(xiàng)式�����,右邊為0
2�、一般形式(及結(jié)構(gòu)名稱):(板書(shū))
a x + b x + c =0 (a,b,c為已知數(shù),a≠0)
說(shuō)明:整理方程的基本步驟是去括號(hào)�����、移項(xiàng)�����、合并同類項(xiàng)��,再由一般形式指出各系數(shù)的值��。
3�、 抽測(cè)題:(1)(2x+1)2=(x+1)(3x+4)
(2) 3
5、x(x-1)=2(x+2)+8
探究三:什么叫一元二次方程的根�?根的意義和作用有哪些應(yīng)用?
1����、根的意義:使方程成立的未知數(shù)的值�����。
2�、根的應(yīng)用:
例題�����, 已知關(guān)于x的一元二次方程的一根為0�,則a的值為( )
A 1 B -1 C 1或-1 D
分析:將x=0代入方程得�����,所以a=1或-1�,又因?yàn)殛P(guān)于x的方程是一元二次方程,所以a-1不等于0�,即a不等于1,故a的值為-1
總結(jié):給出一元二次方程的根�,可以使方程成立,從而能求出方程中的字母系數(shù)���。
探究四:舉例建立實(shí)際應(yīng)用問(wèn)題中的一元二次方程模型�?
1��、 例題 課本29頁(yè)B組第6題
6、
2���、 分析:初步體會(huì)建立一元二次方程模型
題中建立方程等量關(guān)系為容積為2000
底面積 高=2000
總結(jié)拓展
1���、知識(shí)梳理(板書(shū)設(shè)計(jì))
一元二次方程的概念
1、概念:
2�、識(shí)別方法:
3、一般形式:
4���、建模應(yīng)用
2�、當(dāng)堂檢測(cè):《學(xué)法》課后提升
(若學(xué)法未到��,參照下列習(xí)題)
1�����、 請(qǐng)判斷下列方程是否為一元二次方程�����,若是�����,請(qǐng)寫(xiě)出二次項(xiàng)系數(shù)、一次項(xiàng)系數(shù)�����、常數(shù)��。
2�、 已知關(guān)于x的方程 是一元二次方程,求m的值�����,并分別說(shuō)出其二次項(xiàng)系數(shù)�����、一次項(xiàng)系數(shù)���、常數(shù)項(xiàng)。
3�、 課本28頁(yè)A組第2、3題
4�、 課外拓展:(1)課本29頁(yè)B組第7題
(2)若 是關(guān)于x的一元二次方程,求a�����、b的值
5、 教學(xué)反思:
3
 一元二次方程的概念預(yù)導(dǎo)學(xué)案九年級(jí)參考模版修改1
一元二次方程的概念預(yù)導(dǎo)學(xué)案九年級(jí)參考模版修改1